(1571-1630)
Иоганн Кеплер - великий немецкий астроном и математик. Он открыл три основных движения планет, изобрел оптическую систему, применяемую в частности, в современных рефракторах, подготовил создание дифференциального, интегрального и вариационного исчисления в математике.
Иоганн Кеплер родился в городе Вейль-дер-Штадт на юге Германии в бедной протестантской семье. После обучения в монастырской школе в 1596 г. поступил в духовную семинарию при Тюбингенской академии (позднее университет). В эти годы он познакомился с гелиоцентрической системой Н. Коперника. По окончании Академии в 1593 г. Кеплер, обвиненный в свободомыслии, не был допущен к богословской карьере и получил должность школьного учителя математики. В 1600 г. он приехал в Прагу к знаменитому астроному Т. Браге, после смерти которого получил материалы его многчисленных наблюдений.
Кеплер написал много научных трудов и статей. Важнейшее его сочинение - " Новая астрономия " (1609), посвящена изучению движения Марса по наблюдениям Т. Браге и содержащая первые два закона движения планет. В сочинении "Гармония Мира" (1619) Кеплер сформулировал третий закон, объединяющий теорию движения всех планет в стройное целое.
Солнце, занимая один из фокусов эллиптической орбиты планеты, является, по Кеплеру, источником силы, движущей планеты. Он высказал справедливые догадки о существовании между небесными телами тяготения и объяснил приливы и отливы земных океанов воздействием Луны. Составленные Кеплером на основе наблюдений Браге "Рудольфовы таблицы" (1627) давали возможность вычислять для любого момента времени положение планеты с высокой для той эпохи точностью. В работе "Сокращение коперниковой астрономии" (1618-1622) Кеплер изложил теорию и способы предсказания солнечных и лунных затмений. Его исследования по оптике изложены в сочинении "Дополнение к Вителло" (1604) и "Диоптрики" (1611). Замечательные математические способности Кеплера проявились, в частности, в выводе формул для определения объемов многих тел вращения. Рукописи Кеплера были приобретены Петербургской академией наук и хранятся сейчас в России в Санкт-Петербурге.
Список литературы
Для подготовки данной работы были использованы материалы с сайта http://www.physfac.bspu.secna.ru/
Похожие работы
... в 1609, раскрывают характер движения каждой планеты по отдельности, что не удовлетворило Кеплера. Он продолжил поиски «гармонии» в движении всех планет, и спустя 10 лет ему удалось сформулировать третий закон Кеплера. Квадраты звёздных периодов обращения планет относятся между собой как кубы больших полуосей их орбит. Формула, выражающая третий закон Кеплера, такова: A13 ...
... чисел. Арифмометр Лейбница позволил также умножать и делить многозначные числа. Следующий важный шаг в развитии вычислительной техники был сделан только в 20 веке - когда развитие физики позволило создать электронные вычислительные машины (компьютеры). Успехи Кеплера в расчете пройденного планетой пути по известной скорости ее движения стали первым шагом в новой науке - интегральном исчислении. ...
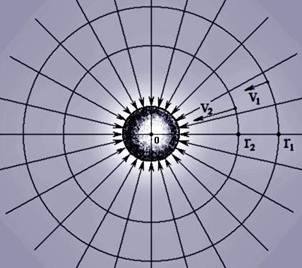
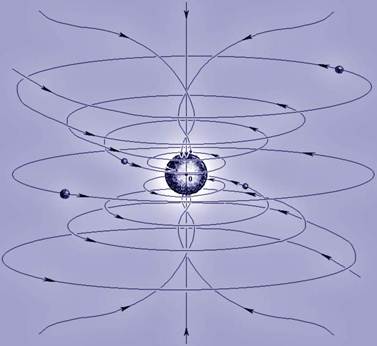
... окружностям экваториальной плоскости равно отношению кубов соответствующих радиусов: T12 / T22 = (r1)3 / (r2)3 . Для материальных объектов, влекомых потоком эфира в неизменной плоскости Лапласа (планет Солнечной системы, к примеру), последняя формула известна как закон Кеплера. Из формулы (4) следует, что константа K = 4 π2 r3 / T2. Для Солнечной системы постоянная K вычисляется наиболее ...
... телескопа, конечно, были счастливейшими в жизни Галилея, такими счастливыми, каких только может пожелать себе человек науки. Каждый день, каждая неделя несли что-нибудь новое… Все прежние представления о Вселенной рушились, все библейские рассказы о сотворении мира становились сказками. Вот Галилей направляет телескоп на Луну и видит не эфирное светило из легких газов, как представляли его себе ...
0 комментариев