Самостоятельная работа № 1
Вариант № 8
1.Вывести аналитическую зависимость теплового эффекта (Дж) реакции от температуры Т:
![]()
Стандартный тепловой эффект ![]() и уравнение зависимости
и уравнение зависимости ![]() из приложения 1.
из приложения 1.
2.Вычислить тепловой эффект при температуре Т=500 К.
3.Построить графики зависимости:
![]()
![]() и
и ![]() - в том интервале температур, для которого справедливо выведенное уравнение зависимости
- в том интервале температур, для которого справедливо выведенное уравнение зависимости ![]()
4.Определить графически ![]() как
как ![]() при
при ![]() и сравнить полученный результат с рассчитанным по формуле
и сравнить полученный результат с рассчитанным по формуле ![]()
Решение.
Таблица 1
| Вещество |
|
| Температурный интервал | ||
|
|
|
| |||
|
| -601,49 | 48,98 | 3,14 | -11,44 | 298…3000 |
|
| -241,8 | 30,0 | 10,71 | 0,33 | 298…2500 |
|
| -924,6 | 46,99 | 102,85 | - | 298…541 |
|
| - | 78,98 | 13,85 | -11,11 | 298…541 |
|
| - | 46,99 | 102,85 | - | 298…2500 |
|
| -16,9 | 31,99 | -89 | -11,11 | 298…2500 |
|
| 81,3 | - | - | - | |
Из данных, приведенных в таблице, получаем:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Проверяем ![]()
С учетом последнего выражения найдем ![]() интегрированием уравнения Кирхгофа в пределах от 298 до Т (Т £ 1000):
интегрированием уравнения Кирхгофа в пределах от 298 до Т (Т £ 1000):
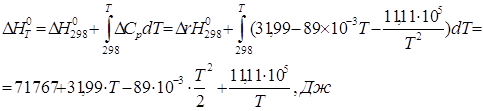
Результаты расчетов по уравнениям представлены в табл. 2.
Таблица 2
| T, К |
|
|
|
|
| 300 | 70,791 | 77,760 | -6,969 | 81060 |
| 325 | 72,963 | 80,331 | -7,368 | 80880 |
| 350 | 74,758 | 82,903 | -8,145 | 80690 |
| 375 | 76,273 | 85,474 | -9,201 | 80470 |
| 400 | 77,576 | 88,046 | -10,47 | 80220 |
| 425 | 78,715 | 90,618 | -11,903 | 79440 |
| 450 | 79,726 | 93,189 | -14,74 | 79620 |
| 475 | 80,635 | 95,761 | -15,126 | 79260 |
| 500 | 81,461 | 98,332 | -16,871 | 78860 |
| 525 | 82,222 | 100,90 | -18,678 | 78410 |
| 541 | 82,667 | 102,55 | -19,883 | 77920 |
На рис. 1 и 2 представлено изменение ![]() ;
; ![]() и
и ![]() в зависимости от температуры, а также определение
в зависимости от температуры, а также определение ![]() при Т1 = 310 К.
при Т1 = 310 К.
Строим графики зависимостей:
![]()
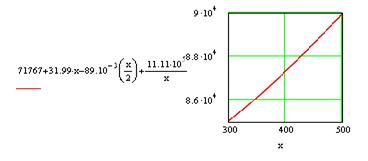
![]() и
и ![]()
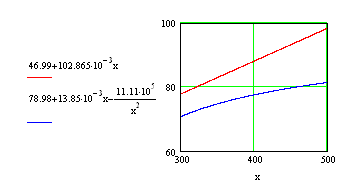
Определяем графически![]() , как
, как ![]() при
при ![]() и сравниваем полученный результат с рассчитанным по формуле
и сравниваем полученный результат с рассчитанным по формуле

![]()
по модулю ![]()
Самостоятельная работа № 2
Вариант № 8
В таблице 1 для некоторого чистого вещества ![]() приведены молекулярная масса
приведены молекулярная масса ![]() (кг/кмоль), плотности в твердом и жидком состояниях (
(кг/кмоль), плотности в твердом и жидком состояниях (![]() и
и ![]() в кг/м3) при температуре трехфазного равновесия (тройная точка), и экспериментальные данные [2] по упругости паров над твердым и жидким веществом при разных температурах. Необходимо:
в кг/м3) при температуре трехфазного равновесия (тройная точка), и экспериментальные данные [2] по упругости паров над твердым и жидким веществом при разных температурах. Необходимо:
1) по графикам зависимостей ![]() от
от ![]() или аналитически рассчитать численные значения постоянных коэффициентов в интегральных уравнениях Клаузиуса — Клапейрона
или аналитически рассчитать численные значения постоянных коэффициентов в интегральных уравнениях Клаузиуса — Клапейрона
![]()
2) вычислить средние для исследованных интервалов температур теплоты испарения, возгонки и плавления; определить координаты тройной точки (параметры трехфазного равновесия);
3) вычислить величину ![]() , характеризующую наклон линии фазового равновесия "
, характеризующую наклон линии фазового равновесия "![]() " в тройной точке;
" в тройной точке;
4) построить диаграмму фазовых равновесий вещества;
5) вычислить температуру плавления вещества при заданном внешнем давлении Р (Па) и оценить нормальную температуру кипения;
6) рассчитать изменение внутренней энергии, энтальпии, свободных энергий Гиббса и Гельмгольца для процесса равновесной возгонки 1 моля вещества при температуре тройного равновесия.
Таблица 1
| Вариант | Твёрдое состояние | Жидкое состояние | Условия | ||
| | |
|
| ||
| 8 | 276,6 278,2 279,2 280,2 281,4 | 1413 1706 1879 2066 2372 | 277,2 279,2 281,4 283,2 285,2 288,7 | 1826 2082 2372 2626 2932 3279 |
|
Решение:
1. Интегрирование уравнения Клаузиуса — Клапейрона в предположении постоянства теплот испарения и возгонки ![]() ,
, ![]() дает выражения:
дает выражения:
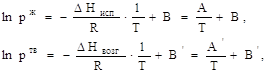
потенцирование, которых приводит к зависимости в явном виде давлений насыщенных паров от температуры:
![]()
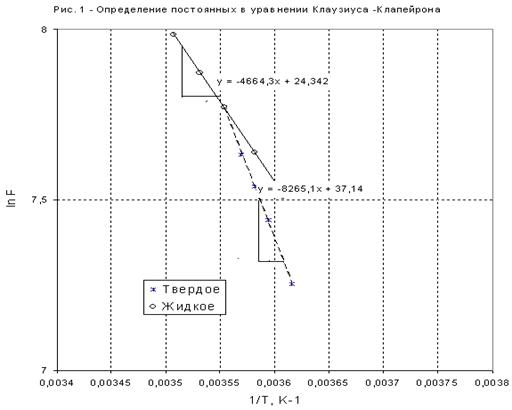
Графики линейных зависимостей ![]() от
от ![]() представлены на рис. 3 по данным, приведенным в табл. 5.
представлены на рис. 3 по данным, приведенным в табл. 5.
По положению прямых на рис. 3 возможно графическое определение постоянных А и В в уравнениях ![]() . После чего теплоты испарения и возгонки можно определить из соотношений:
. После чего теплоты испарения и возгонки можно определить из соотношений: ![]() и
и ![]() . Такие расчеты связаны с ошибками из-за достаточно произвольного проведения прямых линий по экспериментальным точкам.
. Такие расчеты связаны с ошибками из-за достаточно произвольного проведения прямых линий по экспериментальным точкам.
Для более точного аналитического расчета параметров уравнения Клаузиуса — Клапейрона воспользуемся методом наименьших квадратов. Постоянные А и В уравнения ![]() , где
, где ![]() и
и ![]() , можно рассчитать из известных соотношений:
, можно рассчитать из известных соотношений:
Таблица 5
| Равновесие твёрдое вещество — газ | |||||||
|
|
|
|
|
|
|
|
|
| 1 | 1413 | 7,2535 | 276,6 | 0,00361 | 1,300×10–5 | 0,0261 | 1421 |
| 2 | 1706 | 7,4419 | 278,2 | 0,00359 | 1,288×10–5 | 0,0267 | 1687 |
| 3 | 1879 | 7,5385 | 279,2 | 0,00358 | 1,281×10–5 | 0,0271 | 1877 |
| 4 | 2066 | 7,6334 | 280,2 | 0,00356 | 1,267×10–5 | 0,0274 | 2086 |
| 5 | 2372 | 7,7715 | 281,4 | 0,00355 | 1,260×10–5 | 0,0279 | 2365 |
| n = 5 | 37,6388 | 0,01789 | 6,396∙10–5 | 0,1352 | |||
Равновесие жидкость — газ
| i |
|
|
|
|
|
|
|
| 1 | 1826 | 7,50988 | 277,2 | 0,00360 | 1,296×10–5 | 0,0270 | 1836,324 |
| 2 | 2082 | 7,64108 | 279,2 | 0,00358 | 1,281×10–5 | 0,0273 | 2071,554 |
| 3 | 2372 | 7,77148 | 281,4 | 0,00355 | 1,260×10–5 | 0,0275 | 2360,579 |
| 4 | 2626 | 7,87321 | 283,2 | 0,00353 | 1,246×10–5 | 0,0277 | 2622,843 |
| 5 | 2932 | 7,98344 | 285,2 | 0,00350 | 1,225×10–5 | 0,0279 | 2943,963 |
| 6 | 3279 | 8,09529 | 288,7 | 0,00346 | 1,197×10–5 | 0,0281 | 3589,551 |
| n = 6 | 46,874 | 0,02122 | 7,511×10–5 | 0,1655 |
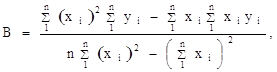
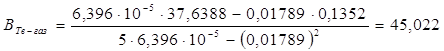
![]()
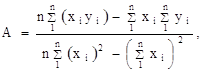
![]()
![]()
где n — число измерений. При использовании данных таблицы получим:
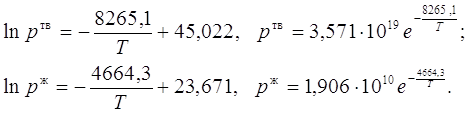
2. Из полученных уравнений рассчитываем среднюю теплоту испарения и возгонки:
![]()
![]() .
.
Теплоту плавления вещества в тройной точке найдем по закону Гесса:
DНпл = DНвозг – DНисп = 68716,04−38776,49=29939,55 Дж/моль.
3. Вычислим dT/dp в тройной точке из уравнения:
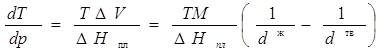
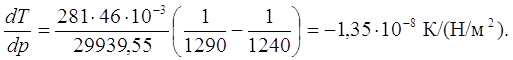
Координаты тройной точки определяем совместным решением уравнений:
Ттр.т = 281 К; Ртр.т = 2289,5 Н/м2.
4. На рис. 4 приведены кривые зависимостей давлений насыщенного пара от температуры для твердого и жидкого вещества, рассчитанные по уравнениям . Эти линии определяют параметры фазовых равновесий «тв ® газ» и «ж ® газ». При имеющейся информации линию фазовых равновесий «тв ® ж» проводим с учетом углового коэффициента этой линии в тройной точке
![]() ,
,
который считается независящим от давления (температуры). Получается практически вертикальная линия с неуловимым наклоном вправо. На диаграмме представлены исходные экспериментальные данные.
5. Температуру плавления вещества при давлении ![]() вычислим по формуле:
вычислим по формуле:
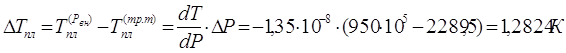
Отсюда ![]()
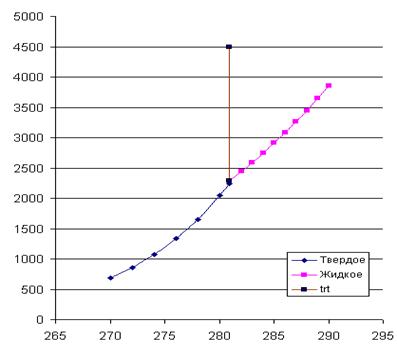
Рис. 2. Температурная зависимость давлений насыщенного пара для твердого и жидкого вещества
Нормальную температуру кипения вещества оценим, подставив в уравнение ![]() . Получим
. Получим
![]()
6. Изменение термодинамических функций для процесса равновесной возгонки 1 моля вещества при условиях трехфазного равновесия составят:
| Энергии Гиббса |
|
| Энергии Гельмгольца |
|
| Энтальпии |
|
| Внутренней энергии |
|
Самостоятельная работа № 3
Вариант № 8
1. Выразить ![]() и
и![]() через равновесное число молей продукта х, если исходные вещества А и В взяты в стехиометрических количествах при общем давлении равновесной газовой смеси Р и температуре Т, К;
через равновесное число молей продукта х, если исходные вещества А и В взяты в стехиометрических количествах при общем давлении равновесной газовой смеси Р и температуре Т, К;
2. Рассчитать ![]() и
и ![]() при 300 К, если
при 300 К, если ![]()
3. Вычислить равновесное количество вещества С при давлении в равновесной системе ![]() и рассчитайте степень превращения вещества А и В.
и рассчитайте степень превращения вещества А и В.
A + B = 3C
Решение:
| А | В | 3С |
|
|
|
|
1)![]() , что говорит о том, что смесь неравновесная
, что говорит о том, что смесь неравновесная
![]()
Равновесные парциальные давления определим по закону Дальтона:
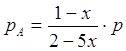 ;
;
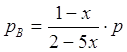 ;
;
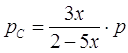
где ![]() - общее давление. Закон действующих масс для данной реакции запишется так:
- общее давление. Закон действующих масс для данной реакции запишется так:
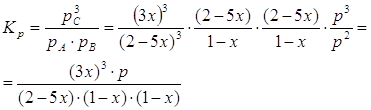
Константу ![]() находим из соотношения:
находим из соотношения:
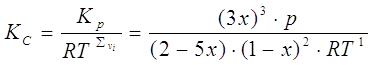
2) Расчет ![]() и
и ![]() при заданной температуре, давлении и известном значении х
при заданной температуре, давлении и известном значении х
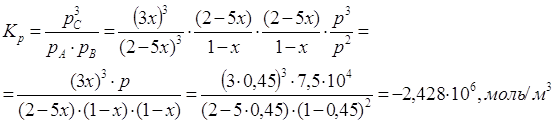
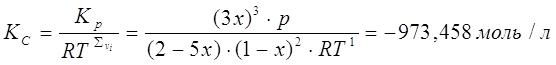
3) При изменении давления изменяется параметр х, температура остаётся неизменной, значение ![]() не меняется.
не меняется.
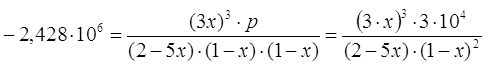
![]() молей
молей
Равновесное количество вещества равно:
![]() молей
молей
Рассчитаем степень превращения веществ А и В:
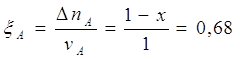
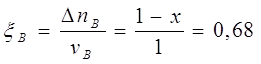
![]() , условие выполнено.
, условие выполнено.
Самостоятельная работа №4
Вариант № 8
Гетерогенная реакция между веществами А и В (табл. 1) протекает при постоянной температуре Т;
1) определите стандартное сродство![]() веществ А и В при 298 К;
веществ А и В при 298 К;
2) вычислите константы равновесия ![]() и
и ![]() при температуре Т;
при температуре Т;
3) определите количество прореагировавшего твёрдого вещества А, если объём системы V м3, а исходное давление газа В равно Р1, объёмом твердой фазы можно пренебречь;
4) определите изменение энергии Гиббса, для начала реакции, если исходное давление газообразных веществ В и С соответственно равны Р2 и Р3, реакция протекает при температуре Т, К идеально обратимо.
Таблица 1
| Реакция | Т, К |
|
|
|
|
|
| 773 | 10 | 705 | 800 | 2 |
Решение:
![]()
|
|
|
|
|
|
|
|
1) Вычисление стандартного сродства ![]() веществ А и В при 298 К;
веществ А и В при 298 К;
![]()
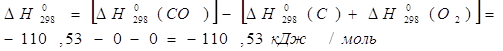
![]()
![]()
2)Вычисление констант равновесия ![]() и
и ![]() при температуре 773 К.
при температуре 773 К.
![]()
![]()
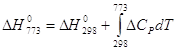
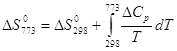
| Вещество |
|
| Температурный интервал | ||
|
|
|
| |||
|
| 0 | 16,86 | 4,77 | – 8,54 | 298…2500 |
|
| 0 | 31,46 | 3,39 | – 3,77 | 298…3000 |
|
| -110,53 | 28,41 | 4,10 | – 0,46 | 298…2500 |
|
| - | 28,41 | 4,10 | – 0,46 | 298…2500 |
|
| - | 48,32 | 8,16 | 12,31 | 298…2500 |
|
| -9,47 | – 19,91 | –4,06 | –12,77 | 298…2500 |
![]()
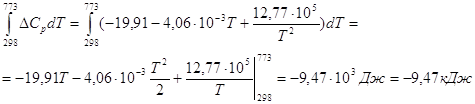
![]()
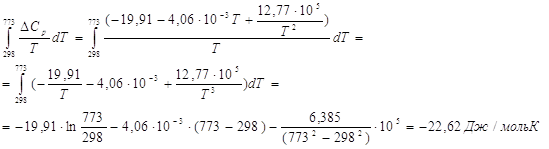
![]()
![]()
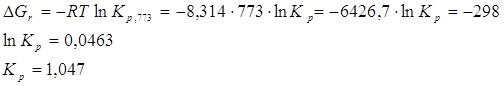
Константу равновесия ![]() можно найти из соотношения:
можно найти из соотношения:
![]()
3)Определение количества прореагировавшего твёрдого углерода, если объём системы ![]() м3, а исходное давление газа
м3, а исходное давление газа ![]() равно
равно ![]() Па
Па
![]() , что говорит о том, что смесь неравновесная
, что говорит о том, что смесь неравновесная
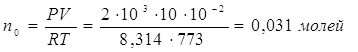
|
|
|
|
|
|
| 2 |
![]() ,
,
![]()
Равновесные парциальные давления определим по закону Дальтона:
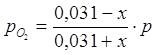 ;
;
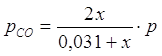 ;
;
где ![]() - общее давление. Закон действующих масс для данной реакции запишется так:
- общее давление. Закон действующих масс для данной реакции запишется так:
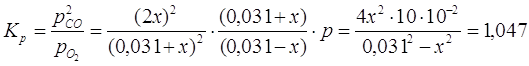
![]()
С учетом того, что углерода расходуется в 2 раза больше, чем кислорода, то количество прореагировавшего углерода составит 0,005 молей.
4) Определение изменения энергии Гиббса для начала реакции
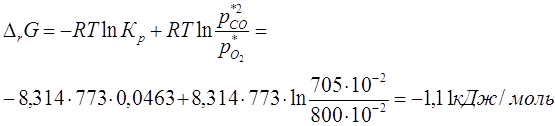
Самостоятельная работа № 5
Вариант 8
Зависимость константы равновесия реакции от температуры (табл. 9) выражается уравнением ![]() коэффициенты a, b, c и d приведены в табл. 1, давление выражено в Паскалях:
коэффициенты a, b, c и d приведены в табл. 1, давление выражено в Паскалях:
1. определите константу равновесия реакции при Т, К;
2. постройте график зависимости ![]() в интервале температур от (Т – 100) до (Т + 100) К;
в интервале температур от (Т – 100) до (Т + 100) К;
3. укажите, как изменяется константа равновесия при повышении температуры;
4. определите тепловой эффект реакции ![]() при Т, К;
при Т, К;
5. сопоставьте тепловой эффект, вычисленный в п. 4, с тепловым эффектом, вычисленным по закону Кирхгофа при температуре Т, К;
6. определите стандартное сродство реагирующих веществ при температуре Т, К.
| Реакция (А) | К | Т, К |
|
|
| 500 |
Таблица 1
| a | b | c | d |
| – 4600 | 0,623 | – 0,001 02 | 17,776 |
Решение:
1)Определение константы равновесия при 500 К.
Заменяем десятичный логарифм натуральным, для чего умножаем обе части уравнения на ![]() .
.
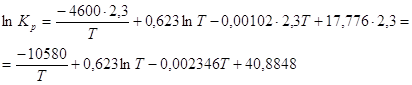
Подставляем значение Т в полученное уравнение:
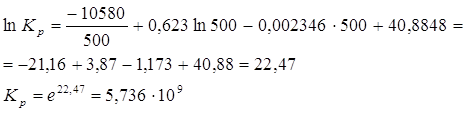
2)Построение графика зависимости ![]() в интервале температур от 400 до 600 К;
в интервале температур от 400 до 600 К;
|
|
|
|
|
|
|
| 400 | 7,489 | 475 | 9,724 | 550 | 10,558 |
| 425 | 8,156 | 500 | 9,747 | 575 | 10,908 |
| 450 | 8,747 | 525 | 10,173 | 600 | 11,228 |
3) Константа равновесия при повышении температуры увеличивается. Принимаем Т=1000К и повторяем расчет. Функция экспоненты в степени х является возрастающей, значит чем больше значение логарифма функции, тем больше сама функция.
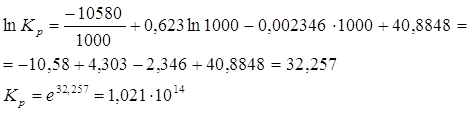
4)Определение стандартного теплового эффекта при Т=500К
![]()
![]()
![]()
5)Сопоставление теплового эффекта, вычисленного в п. 4, с тепловым эффектом, вычисленным по закону Кирхгофа при температуре 500 К;
Сначала вычисляем стандартный тепловой эффект при 298 К.
![]()
![]()
Вычисление теплоёмкостей конечных и исходных продуктов реакции. Значения ![]() и
и ![]() взяты из приложения 1 методического пособия.
взяты из приложения 1 методического пособия.
![]()
![]()
![]()
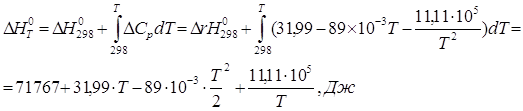
![]()
![]()
Небольшая разница возникает из-за погрешности вычисления.
6) Вычисление стандартного сродства ![]() веществ А и В при 500 К;
веществ А и В при 500 К;
![]()
Самостоятельная работа №7
Вариант № 8
Вычислите константу равновесия Кр реакции при заданной температуре Т. Для расчета воспользоваться методом Темкина — Шварцмана и прил. 1 и 2.
| Реакция | Т, К |
|
| 400 |
Воспользуемся формулой:
![]()
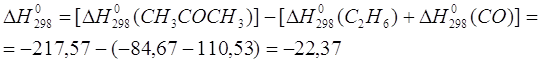
![]()
| Вещество |
| |||
|
|
|
|
| |
|
| 5,75 | 175,11 | — | – 57,85 |
|
| 28,41 | 4,10 | – 0,46 | — |
|
| 22,47 | 201,80 | — | – 63,50 |
|
| 22,47 | 201,80 | — | – 63,50 |
|
| 34,16 | 179,21 | – 0,46 | – 57,85 |
|
| −11,69 | 22,59 | – 0,46 | – 5,65 |
![]()
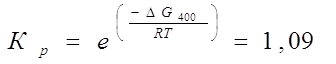
Похожие работы
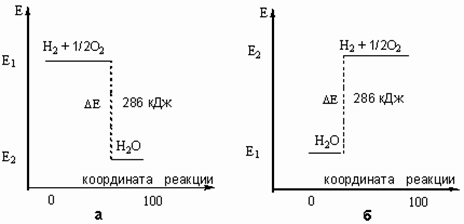
... в уравнениях реакций и не забывать о том, что складываемые, вычитаемые или сокращаемые моли вещества должны находиться в одинаковом агрегатном состоянии. 2. Применение теплового эффекта на практике Тепловые эффекты химических реакций нужны для многих технических расчетов. Например, рассмотрим мощную российскую ракету "Энергия", способную выводить на орбиту космические корабли и другие полезные ...
... коэффициенты в уравнениях реакций и не забывать о том, что складываемые, вычитаемые или сокращаемые моли вещества должны находиться в одинаковом агрегатном состоянии. 2. Применение теплового эффекта на практике Тепловые эффекты химических реакций нужны для многих технических расчетов. Например, рассмотрим мощную российскую ракету "Энергия", способную выводить на орбиту космические корабли и ...
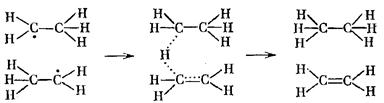
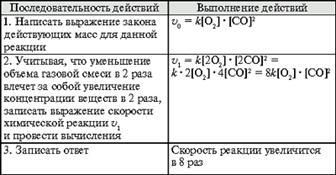
... , т. е. к увеличению скорости реакции. Количественно зависимость между скоростью реакции и молярными концентрациями реагирующих веществ описывается основным законом химической кинетики — законом действующих масс. Скорость химической реакции при постоянной температуре прямо пропорциональна произведению концентраций реагирующих веществ. Для мономолекулярной реакции скорость реакции ...
... условия сдвига равновесия вправо .... Глава 2. Прикладные аспекты преподавания темы «Закономерности течения химических реакций» Прикладные аспекты преподавания темы «Закономерности течения химических реакций» на мой взгляд удобнее всего рассматривать на уроках, которые следуют сразу за рассмотрением скорости реакции и химического равновесия, - это производство серной кислоты. 2.1 ...


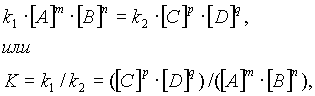



0 комментариев