Состояние изотермической системы с неизменным объёмом целесообразно описывать посредством свободной энергии (функции Гельмгольца). В этих условиях она является характеристической функцией и изохорно-изотермическим потенциалом системы.
Посредством частного дифференцирования из неё далее можно извлечь прочие необходимые термодинамические характеристики, а именно:
![]() (1)
(1)
Построить явный вид функции свободной энергии для некоторых относительно простых систем можно методом статистической термодинамики.
В любом естественно протекающем (самопроизвольном или свободном) процессе свободная энергия системы понижается. При достижении системой состояния термодинамического равновесия её свободная энергия достигает минимума и уже в равновесии далее сохраняет постоянное значение. Из равновесия систему можно вывести за счёт внешних сил, повышая её свободную энергию. Такой процесс уже не может быть свободным - он будет вынужденным.
Микроскопические движения частиц и в равновесии не прекращаются, и в системе, состоящей из огромного числа частиц и подсистем любой природы, возможно множество различных частных вариантов и комбинаций отдельных частей и внутри них, но все они не выводят систему из равновесия.
Термодинамическое равновесие в макросистеме совсем не означает, что и в её микроскопических фрагментах исчезают все виды движения. Напротив, равновесие обеспечивается динамикой именно этих микроскопических движений. Они-то осуществляют непрерывное выравнивание - сглаживание наблюдаемых макроскопических признаков и свойств, не допуская их выбросов и чрезмерных флуктуаций.
Основной целью статистического метода является установление количественной связи между характеристиками механических движений отдельных частиц, составляющих равновесный статистический коллектив, и усреднёнными свойствами этого коллектива, которые доступны для термодинамических измерений макроскопическими методами.
Цель состоит в том, чтобы на основании механических характеристик движений отдельных микроэлементов равновесного коллектива вывести количественные законы для термодинамических параметров системы.
Согласно методу Гиббса термодинамическая система это коллектив - совокупность очень большого числа элементов - однотипных подсистем.
Каждая подсистема в свою очередь может также состоять из очень большого числа иных ещё более мелких подсистем и в свою очередь может играть роль вполне самостоятельной системы.
Все естественные флуктуации внутри равновесной системы равновесия не нарушают, они совместимы с устойчивым макроскопическим состоянием огромного коллектива частиц. Они просто перераспределяют признаки отдельных элементов коллектива. Возникают разные микросостояния, и все они суть версии одного и того же наблюдаемого макросостояния.
Каждая отдельная комбинация состояний элементов коллектива порождает лишь одно из огромного множества возможных микросостояний макросистемы. Все они в физическом смысле равноценны, все приводят к одному и тому же набору измеримых физических параметров системы и отличаются лишь какими-то деталями распределения состояний между элементами …
Все микросостояния совместимы с макроскопическим - термодинамическим равновесием, и числовой разброс отдельных составляющих свободной энергии (её энергии и энтропии) является вполне обычным обстоятельством. Надо понимать, что разброс возникает за счёт непрерывного обмена энергией между частицами – элементами коллектива. У одних элементов она уменьшается, но при этом у других увеличивается.
Если система находится в термостате, то ещё непрерывно осуществляется обмен энергией и с окружающей средой. Происходит естественное энергетическое перемешивание коллектива, за счёт непрерывного обмена между микрочастицами коллектива. Равновесие постоянно поддерживается через тепловой контакт с внешним термостатом. Так в статистике чаще всего именуют окружающую среду.
Создавая универсальную схему статистической механики, Гиббс использовал удивительно простой приём.
Любая реальная макроскопическая система это коллектив из огромного множества элементов – подсистем. Подсистемы могут иметь и макроскопические размеры, и могут быть микроскопическими, вплоть до атомов и молекул. Всё зависит от рассматриваемой задачи и уровня исследования.
В разные моменты времени в разных точках реальной системы, в разных пространственных регионах макроскопического коллектива мгновенные характеристики его малых элементов могут быть различны. «Неоднородности» в коллективе постоянно мигрируют.
Атомы и молекулы могут находиться в разных квантовых состояниях. Коллектив огромный, и в нём представлены различные комбинации состояний физически одинаковых частиц. На атомно-молекулярном уровне всегда происходит обмен состояниями, имеет место их непрерывное перемешивание. Благодаря этому свойства различных фрагментов макроскопической системы выравниваются, и физически наблюдаемое макроскопическое состояние термодинамической системы внешне выглядит неизменным...
Броуновское движение – главный молекулярный механизм, обеспечивающий перемешивание локальных свойств микроскопических подсистем - элементов макроскопического коллектива. Броуновское движение и ряд сопутствующих ему релаксационных процессов выравнивают в пространстве и усредняют во времени суммарные динамические характеристики макроскопического равновесного коллектива, превращая их в измеримые термодинамические параметры с равновесными значениями.
Так возникает огромное множество мгновенных различающихся суммарных состояний всего коллектива, и все они совместимы с одним и тем же внешне неизменным термодинамическим равновесием системы.
Всё множество, сколь необозримым оно бы не казалось, всевозможных комбинаций микромеханических состояний всех однотипных элементов системы, совместимых с её термодинамическими характеристиками в её определённом наблюдаемом термодинамическом (макроскопическом) состоянии, Гиббс определил как АНСАМБЛЬ.
Ансамбль напоминает ленту бесконечного фильма, кадры котрого, время от времени повторяясь, с бесконечными вариациями изображают одну и ту же сцену с некоторыми изменениями. Элементы ансамбля подобны отдельным кадрам этого бесконечного фильма.
Весь ансамбль изображает макросостояние (фильм), а его элементы суть микросостояния (кадры этого фильма).
Рассмотрим пробег химической реакции между несколькими частицами:
![]() (2)
(2)
Следуя правилам IUPAC, стехиометрические коэффициенты представим в виде массива
ni Î (-a, - b,… +k, +m, …); (3)
Стандартное сродство (стандартное приращение энергии Гиббса) определяется через стандартные химические потенциалы реагентов и продуктов и изотермой Вант-Гоффа связано с безразмерной термодинамической константой равновесия Kp:
![]() ; (4)
; (4)
Это и есть основание для расчёта константы химического равновесия.
Применяя правило ИЮПАК для стехиометрических коэффициентов, формулу (21.3) легко записать в общем виде
![]() ; (5)
; (5)
Введём стандартные химические потенциалы ![]() веществ i.
веществ i.
![]() . (6)
. (6)
Стандартное сродство реакции принимает вид
![]() ; (7)
; (7)
Сокращая на RT=NkT, получаем
![]() ; (8)
; (8)
Константа химического равновесия в смеси идеальных газов.
Совершим цепочку несложных преобразований. Вначале внесём стехиометрические коэффициенты в сумме под знак логарифма в виде показателей степеней у статистических сумм
![]() ; (9)
; (9)
Затем воспользуемся тем, что сумма логарифмов равна логарифму произведения
![]() ; (10)
; (10)
Наконец, избавляясь от логарифмов, получаем искомое статистическое выражение для константы равновесия
![]() ; (11)
; (11)
Она имеет вид произведения статистических сумм.
Константа химического равновесия в смеси идеальных газов.
![]()
![]() ; (12)
; (12)
Стандартные суммы состояний имеют вид:
- трансляционная: 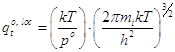 ; (13)
; (13)
- молекулярная: 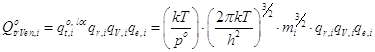 ; (14)
; (14)
Константа равновесия может рассчитываться как непосредственно в виде произведения статистических сумм,
![]() ; (15)
; (15)
которые предварительно следует рассчитать, а также по результирующей формуле
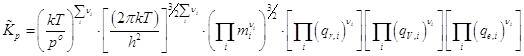 ; (21.14)
; (21.14)
При вычислении электронных сумм состояния помним, что занят один-единственный электронный уровень, и он характеризуется кратностью вырождения ge, i. Эта кратность равна числу микросостояний основного терма у атомов и у молекул. У молекул чаще всего достаточно спиновой мультиплетности, но возможно и орбитальное вырождение. Это уже зависит от конкретной частицы.
Поэтому электронная сумма состояний у молекулы определяется формулой
![]() ; (16)
; (16)
Энергия химической связи считается равной энергии её диссоциации и отсчитывается от основного колебательного уровня, а не от минимума потенциальной кривой.
Этот вопрос рассмотрен в учебнике Даниэльса и Олберти на стр.539 в разделе 17.13. Там же приводятся основные формулы. Раздел написан хорошо и достаточно просто. Этот учебник вполне пригоден для подготовки студентов.
1. Сводка статистических сумм для простейших стационарных движений.
ПРИЛОЖЕНИЕ 1. Математическая справка о факториалах больших числах.
Факториал числа, соизмеримого с числом Авогадро, непосредственно вычислить невозможно, и поэтому давно разработаны приближённые способы численно точного вычисления, основанные на применении гамма – функции Эйлера первого рода.
При очень большом числе, факториал которого вычисляется, точной становится формула Стирлинга (можете проверить прямыми вычислениями). Разность между точным и приближённым логарифмами становится относительно малой величиной:
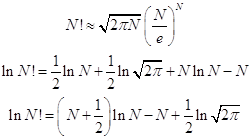
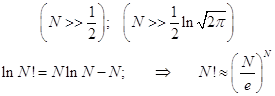
Таблица. Точные и приближённые значения логарифмов факториалов больших чисел.
| N | N! точно | ln(N!) точно | Стирлинг точно | Стирлинг прибл. |
| 8 | 40320 | 10.604 | 10.594 | 8.635 |
| 9 | 362880 | 12.802 | 12.7925 | 10.775 |
| 10 | 3628800 | 15.1044 | 15.096 | 13.026 |
| 11 | 39916800 | 17.5023 | 17.4948 | 15.377 |
| 12 | 479001600 | 19.987 | 19.979 | 17.818 |
| 13 | 6227020800 | 22.55216 | 22.545 | 20.344 |
| 14 | 8.71782912*1010 | 25. 19122 | 25.185 | 22.947 |
| 20 | 2.432902008*1018 | 42.3356 | 42.33145 | 39.915 |
| 25 | 1.55112100*1025 | 58.00 | 57.998 | 55.470 |
| 50 | 3.041409*1064 | 148.478 | 148.476 | 145.601 |
ПРИЛОЖЕНИЕ 2.
Дополнительные сведения о вращательных статистических суммах.
Для справки приведём ротационные статистические суммы молекулы с учётом её внутренних вращений
Суммы по состояниям для внутреннего вращения (Ерёмин, стр.181-182):
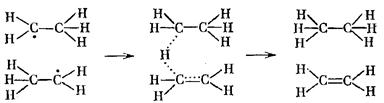
Для свободного внутреннего вращения в этане (при высокой температуре):
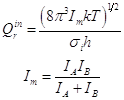
Для каждой из двух свободно вращающихся групп в сложной молекуле:
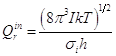
Число молекулярной вращательной симметрии требует специального анализа. Там же у Ерёмина приводятся приёмы расчёта.
Учитывая все ротационные преобразования симметрии, например, для этана получаем число 18 (3 степени свободы для вращения вокруг оси 3-го порядка вдоль связи C-C, ещё 2 - для оси 2-го порядка и также для внутреннего вращения – вновь ось 3-го порядка).
Вся ротационная сумма состояний в общем случае приобретает вид:
(Ерёмин, стр.233, формула VI.155)
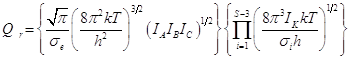 .
.
Множитель p1/2 появляется при вычислении ротационной статистической суммы методом классической статистики, тогда как вывод общей формулы на основе квантовой статистики невозможен.
Вращательные стат. суммы сложных молекул и ротационное число симметрии.
(см. Приложение – несколько страниц из книги Дж. Майер, М. Гёпперт-Майер).
Похожие работы
... , т. е. к увеличению скорости реакции. Количественно зависимость между скоростью реакции и молярными концентрациями реагирующих веществ описывается основным законом химической кинетики — законом действующих масс. Скорость химической реакции при постоянной температуре прямо пропорциональна произведению концентраций реагирующих веществ. Для мономолекулярной реакции скорость реакции ...
... газа, позволяющий регенерировать сернистый ангидрид независимо от его концентрации в технологических газах; основные характеристики: полная автоматизация процесса, возможность использования тепла реакции окисления сернистого ангидрида для получения товарного пара и полная экологическая чистота). Длительное время лучшим катализатором считался платиновый, однако с 1932 г. его вытеснили ванадиевые. ...
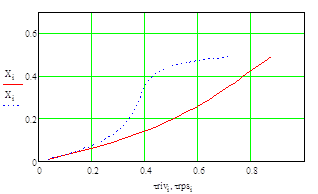
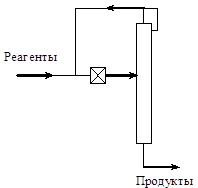
... использовать идеализированный массообменный процесс, позволяющий осуществлять полное отделение продуктов реакции от реагентов, которые должны быть тем или иным способов возвращены в реакционную зону. Для описания математической модели парожидкостного равновесия (ПЖР) в реальных системах пользуются обобщенным уравнением Рауля: , где γi – коэффициент активности i-го компонента в жидкой фазе ...
... из водяного пара, а из водорода и кислорода, то подобным же образом приходим к тем же результатам. И в том и в другом случае при равенстве скоростей обеих реакций устанавливается химическое равновесие, внешне характеризующееся тем, что концентрации водорода, кислорода и водяного пара при неизменных условиях остаются постоянными сколь угодно долгое время. Из рассмотренного вытекает, что химическое ...
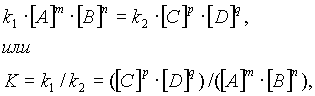


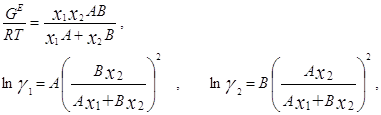
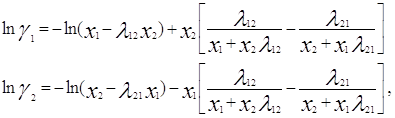
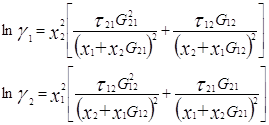
0 комментариев