Навигация
Определение статистических данных
Задача 1
За отчетный период имеются данные о розничном товарообороте и издержках обращения по магазинам торга:
| № магазина | Объем розничного товарооборота, тыс. грн. | Издержки обращения, тыс. грн. | № магазина | Объем розничного товарооборота, тыс. грн. | Издержки обращения, тыс. грн. |
| 1 | 200 | 16,2 | 11 | 570 | 38,9 |
| 2 | 590 | 37,3 | 12 | 472 | 28,6 |
| 3 | 825 | 46,6 | 13 | 278 | 18,2 |
| 4 | 463 | 38,8 | 14 | 665 | 39,0 |
| 5 | 245 | 15,1 | 15 | 736 | 37,8 |
| 6 | 392 | 27,4 | 16 | 562 | 36,6 |
| 7 | 511 | 30,9 | 17 | 338 | 26,7 |
| 8 | 404 | 29,5 | 18 | 560 | 29,0 |
| 9 | 642 | 44,7 | 19 | 695 | 40,0 |
| 10 | 425 | 37,2 | 20 | 580 | 36,5 |
Для выявления зависимости между объемом розничного товарооборота и уровнем издержек обращения сгруппируйте магазины по размеру розничного товарооборота, образовав 5 групп с равными интервалами. По каждой группе и в целом по совокупности магазинов подсчитайте: а) число магазинов; б) объем розничного товарооборота – всего и в среднем на один магазин; в) Сделайте выводы.
Решение
1. Определим величину интервала.
i = (Xmax – Xmin) / n , где
Хmax – максимальный розничный товарооборот;
Xmin – минимальный розничный товарооборот;
n – количество групп;
i = (825 – 200) / 5 = 125;
Определим границы интервалов:
| 1 | ||||
| 200 - 325 | 325 - 450 | 450 - 575 | 575 - 700 | 700 - 825 |
По каждой группе необходимо подсчитать количество магазинов, объем розничного товарооборота – всего и в среднем на один магазин, сумму издержек обращения – всего и на один магазин. и оформить результаты в виде таблицы.
Вывод: Из результатов, приведенных в таблице, видна прямая зависимость между объемом розничного товарооборота и издержками обращения.
| № п/п | Интервалы | №№ магазинов | Объем товарооборота, т.грн | Издержки обращения, т.грн |
| 200 - 325 | 1 | 200 | 16,2 | |
| 5 | 245 | 15,1 | ||
| 13 | 278 | 18,2 | ||
| Итого | 3 | 723 | 49,5 | |
| В среднем по группе | 241 | 16,5 | ||
| 325 - 450 | 17 | 338 | 26,7 | |
| 6 | 392 | 27,4 | ||
| 8 | 404 | 29,5 | ||
| 10 | 425 | 37,2 | ||
| Итого | 4 | 1559 | 120,8 | |
| В среднем по группе | 389,75 | 30,2 | ||
| 450 - 575 | 4 | 463 | 38,8 | |
| 12 | 472 | 28,6 | ||
| 7 | 511 | 30,9 | ||
| 18 | 560 | 29 | ||
| 16 | 562 | 36,6 | ||
| 11 | 570 | 38,9 | ||
| Итого | 6 | 3138 | 202,8 | |
| В среднем по группе | 523 | 33,8 | ||
| 575 - 700 | 20 | 580 | 36,5 | |
| 2 | 590 | 37,3 | ||
| 9 | 642 | 44,7 | ||
| 14 | 665 | 39 | ||
| 19 | 695 | 40 | ||
| Итого | 5 | 3172 | 197,5 | |
| В среднем по группе | 634,4 | 39,5 | ||
| 700-825 | 15 | 736 | 37,8 | |
| 3 | 825 | 46,6 | ||
| Итого | 2 | 1561 | 84,4 | |
| В среднем по группе | 780,5 | 42,2 | ||
| Всего | 20 | 10153 | 655 | |
| В среднем по совок-ти на 1 магазин | 507,65 | 32,8 | ||
Задача 2
Имеются следующие данные о распределении заводов области по уровню коэффициента сменности:
| № п/п | Группа предприятий по уровню коэффициента сменности работы оборудования | Число единиц оборудования, % | Середина интервала |
| 1 | До 1,7 | 2,2 | 1,65 |
| 2 | 1,7 – 1,8 | 12,8 | 1,75 |
| 3 | 1,8 – 1,9 | 32,6 | 1,85 |
| 4 | 1,9 – 2,0 | 24,9 | 1,95 |
| 5 | 2,0 – 2,1 | 23,4 | 2,05 |
| 6 | 2,1 – 2,2 | 4,1 | 2,15 |
| Итого | 100,0 |
Определить средний уровень коэффициента сменности по области. Сделать выводы.
Решение
Определяем величину интервала i=0,1. Вычисляем середины интервалов. Данные заносим в таблицу.
Среднее средний уровень коэффициента сменности по области определяется по формуле средней арифметической взвешенной.
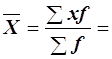 (1,65*2,2+1,75*12,8+1,85*32,6+1,95*24,9+
(1,65*2,2+1,75*12,8+1,85*32,6+1,95*24,9+
+2,05*23,4+2,15*4,1)/100=1,91
Т.о. средний размер затрат на гривну товарной продукции равен 1,91.
Задача 3
Имеются следующие данные о производстве цемента:
| Год | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 |
| Пр-во цемента, млн. т | 33 | 39 | 46 | 51 | 57 | 61 |
Определить аналитические показатели ряда динамики выпуска цемента за 1994 – 1999 г.г.: абсолютные прироста, темпы роста и темпы прироста, абсолютное значение 1% прироста, а также средние обобщающие показатели ряда динамики.
Решение
Основные показатели динамики продукции предприятия
| Годы | Производство продукции, млн.грн. | Абсолютные приросты, млн.грн. | Темпы роста, % | Темпы прироста, % | Абсолютное значение 1% прироста, млн.грн. | |||
| С предыдущ. годом | С 1994г. | С предыдущ. годом | С 1994г. | С предыдущ. годом | С 1994г. | |||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1994 | 33 | - | - | - | 100,00 | 0,00 | - | - |
| 1995 | 39 | 6 | 6 | 118,18 | 118,18 | 18,18 | 18,18 | 0,33 |
| 1996 | 46 | 7 | 13 | 117,95 | 139,39 | 17,95 | 39,39 | 0,39 |
| 1997 | 51 | 5 | 18 | 110,87 | 154,55 | 10,87 | 54,55 | 0,46 |
| 1998 | 57 | 6 | 24 | 111,76 | 172,73 | 11,76 | 72,73 | 0,51 |
| 1999 | 61 | 4 | 28 | 107,02 | 184,85 | 7,02 | 84,85 | 0,57 |
| Итого | 287 | 28 | - | - | - | - | - | - |
Показатель абсолютного прироста определяется по формуле
![]() - по сравнению с предыдущим годом (графа 3);
- по сравнению с предыдущим годом (графа 3);
![]() - по сравнению с предыдущим годом (графа 4),
- по сравнению с предыдущим годом (графа 4),
где ![]() – показатель i-го года;
– показатель i-го года;
![]() – показатель базового года
– показатель базового года
Темпы роста определяются по формуле
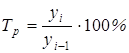 (графа 5) или
(графа 5) или 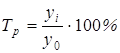 (графа 6).
(графа 6).
Темпы прироста определяются по формуле
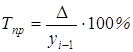 (графа 7) или
(графа 7) или 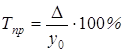 (графа 8).
(графа 8).
Показатель абсолютного значения одного процента прироста
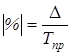 или
или ![]() (графа 9) .
(графа 9) .
Средний уровень ряда в случае равноотстоящих уровней во времени определяется по формуле средней взвешенной простой
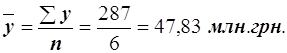
Средний абсолютный прирост
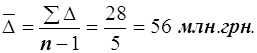
Среднегодовой темп роста
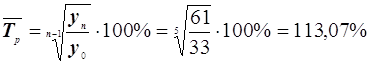 .
.
Среднегодовой темп прироста
![]()
Задача 4
Имеются следующие данные:
| Вид продукции, млн.грн. | Общие затраты на пр-во продукции, млн. грн. | % изменения с/с единицы продукции в отчетном/ базисном периоде | Индекс С/с ip | |
| Базисный период | Отчетный период | |||
| Железо листовое | 460,0 | 544,8 | -1,3 | 0,987 |
| Рельсы трамвайные | 293,0 | 374,5 | +1,2 | 1,012 |
| Чугун передельный | 7,0 | 6,7 | Без изменения | 1 |
Определить: 1) общие индексы себестоимости, затрат на производство и физического объема продукции; 2) общую сумму экономии (перерасхода) за счет изменения себестоимости продукции в отчетном периоде по сравнению с базисным.
Решение
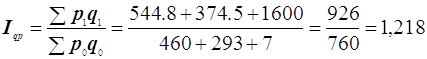 =121,8%
=121,8%
Т.о. ообщие затраты на производство продукции в отчетный период по сравнению с базовым возросли на 21,8%
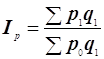 ;
; 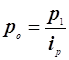
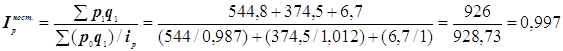 =99,7%
=99,7%
Общие затраты на производство продукции уменьшились на 0,3%, что в абсолютном выражении составляет (926-928,73)=-2,73 млн.грн.
Индекс физического объема находим из взаимосвязи индексов:
Iqp=Iq*; Iq= Iqp: Ip=1.218:0.997=1.222=122,2%
Задача 5
Имеются следующие данные о распределении по выполнению норм выработки механического цеха:
| № п/п | Выполнение норм выработки, % | Количество рабочих в цехе | Середина интервала |
| 1 | 95-100 | 3 | 97,5 |
| 2 | 100-105 | 82 | 102,5 |
| 3 | 105-110 | 157 | 107,5 |
| 4 | 110-115 | 35 | 112,5 |
| 5 | Свыше 115 | 8 | 117,5 |
| Итого | 285 |
Определить: 1) средний процент норм выработки для всего цеха; 2) среднее линейное отклонение; 3) дисперсию и среднее квадратическое отклонение; 4) коэффициент вариации. Сделать выводы.
Решение
1) Средний процент норм выработки для всего цеха определяется по формуле средней арифметической взвешенной
![]() ,
,
где ![]() - значение середины интервала для каждого диапазона выполнения норм;
- значение середины интервала для каждого диапазона выполнения норм;
![]() - количество рабочих в цехе.
- количество рабочих в цехе.
![]() .
.
2) Среднее линейное отклонение определяется по формуле
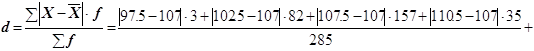
![]()
3) Дисперсия определяется по формуле
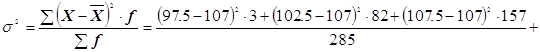
![]() .
.
4) Среднеквадратическое отклонение определяем по формуле
![]() .
.
5) Коэффициент вариации
![]() .
.
Т.о., можно сделать вывод об однородности представленной совокупности данных.
Задача 6
По городской телефонной сети из 1000 абонентов в порядке механической выборки произвели 100 наблюдений и установили, что средняя продолжительность телефонного разговора 4 мин при среднем квадратическом отклонении 2 мин.
Определить: 1) предельную ошибку репрезентативности (с вероятностью 0,954); 2) вероятность того, что предельная ошибка репрезентативности не превысит 0,3 мин.
Решение
N=1000 – генеральная совокупность
n=100 – выборочная совокупность
tср=4 мин. –
σ=2 мин.
Средняя ошибка выборки
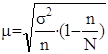
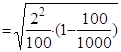 =0,19
=0,19
Δ=t*μ – предельная ошибка
t=2 (коэффициент доверия, которому соответствует вероятность 0,954)
Δ=2*0,19=0,38
Это значит, что с вероятностью 0,954 можно гарантировать, что средняя продолжительность генеральной совокупности телефонных разговоров расположится между 3,62 мин. и 4,38 мин.
Задача № 1
1) Определим величину интервала
I=(8,1-0,5) :4=7,6:4=1,9
Количество заводов по группам.
| № группы | Группировка заводов | Среднегодовая стоимость | Валовая продукция в сопоставимых ценах, грн. | Уровень фондоотдачи (%) | |||
| к-во шт. | № № | всего | на завод | всего | на завод | ||
| 1 | 5 | 1,8,12,13,20 | 5,0 | 1,0 | 4,5 | 0,9 | 90 |
| 2 | 8 | 2,3,5,7,9,11,22,23, | 26,9 | 3,3625 | 26,8 | 3,35 | 99,6 |
| 3 | 6 | 4,6,10,15,18,21 | 30,3 | 13,3 | 35 | 5,833 | 115,5 |
| 4 | 5 | 14,16,17,19,24 | 34,8 | 6,96 | 34,5 | 6,9 | 99 |
2) Интервал для групп заводов:
1-я :0,5…2,4
2-я :2,4…4,3
3-я :4,3…6,2
4-я :6,2…8,1
3) Уровень фондоотдачи = (Валовая продукция / стоимость ОФ) * 100%
Выводы:
1) С ростом стоимости основных фондов (ОФ) растет стоимость валовой продукции следовательно между этими показателями существует прямая зависимость.
2) Уровень фондоотдачи не зависит от изменения стоимости ОФ и стоимости валовой продукции.
Задача № 2Имеются данные по двум заводам, вырабатывающим однородную продукцию (табл. 31).
Таблица 31
| Номер завода | 1998 год | 1999 год | ||
| Затраты времени на единицу продукции, ч | Изготовление продукции, шт. | Затраты времени на единицу продукции, ч | Затраты времени на всю продукцию, ч | |
| 1 | 2,0 | 150 | 1,9 | 380 |
| 2 | 3,0 | 250 | 3,0 | 840 |
Вычислите средние затраты времени на изготовление единицы продукции по двум заводам с 1998 по 1999 г.г. Укажите, какой вид средней необходимо применять при вычислении этих показателей.
Решение
Если в статистической совокупности дан признак Xi и его частота fi, то расчет ведется по формуле средней арифметической взвешенной:
![]() (ч)
(ч)
Если дан признак xi , нет его частоты fi, а дан объемM = xifi распространения явления, тогда расчет ведем по формуле средней гармонической взвешенной:
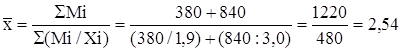 (ч)
(ч)
Вывод: В среднем затраты времени на изготовление единицы продукции в 1998г. выше, чем в 1999г.
Задача 3Для определения средней суммы вклада в сберегательных кассах района, имеющего 9000 вкладчиков, проведена 10%-я механическая выборка, результаты которой представлены в таблице.
| Группы вкладов по размеру, грн. - xi | До 200 | 200-400 | 400-600 | 600-800 | Св.800 | Σ |
| Число вкладчиков - fi | 80 | 100 | 200 | 370 | 150 | 900 |
| Середина интервала | 100 | 300 | 500 | 700 | 700 | |
| x – A=x' - 700 | -600 | -400 | -200 | 0 | +200 | |
| (X - A) / i | -3 | -2 | -1 | 0 | 1 | |
| ((X - A) / I) *f | -240 | -200 | -200 | 0 | 150 | -490 |
| ((X - A) / I)2 *f | 720 | 400 | 200 | 0 | 150 | 1470 |
Решение:
Для определения средней суммы вкладов способов моментов воспользуемся формулой:
![]() = m1Δ*I+Ai
= m1Δ*I+Ai
где: m1 – момент первого порядка
x – варианта
i – величина интервала
f – частота
Δ – постоянная величина, на которую уменьшаются все значения признака.
m1 =(Σ((X-A) / i))*f) / Σf
![]() =(( Σ ((X-A) / i*f) / Σf)*i+A
=(( Σ ((X-A) / i*f) / Σf)*i+A
Похожие работы
... его увеличением для целей информационного обеспечения исполнительных местных органов [7,8]. 3 ОПЫТ УПРАВЛЕНИЯ И ОБОЩЕНИЕ ДАННЫХ НА ПРИМЕРЕ АЛМАТИНСКОГО ОБЛАСТНОГО УПРАВЛЕНИЯ СТАТИСТИКИ3.1 Алматинское областное управление статистики как субъект сбора и обобщения статистической информации В своей деятельности Алматинское областное управление статистики (АОУС) руководствуется ...
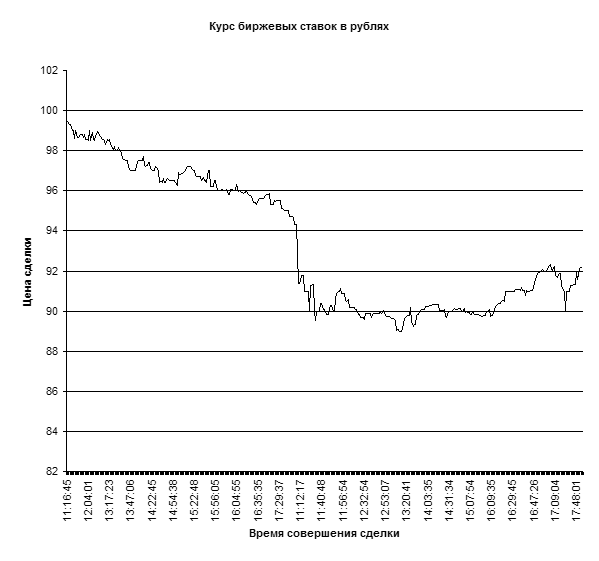
... быстро выполняемой счетной операцией. Данная работа посвящена изучению возможности обработки статистических данных биржевых ставок методами корреляционного и регрессионного анализа с использованием пакета прикладных программ Microsoft Excel. Роль корреляцонно-регрессионного анализа в обработке экономических данных Корреляционный анализ и регрессионный анализ являются смежными разделами ...
... , а также систему показателей, характеризующих изучаемую совокупность явлений и процессов как в целом, так и отдельных ее частей. 1.2 Сущность и классификация группировки статистических данных Группировка является научной основой сводки. В процессе сводки первичный материал разделяется на группы по каким-то варьирующим признакам. Группировкой в статистике называется расчленение изучаемого ...
... макетов статистических таблиц для представления результатов сводки. План статистической сводки содержит указания о последовательности и сроках выполнения отдельных частей сводки, ее исполнителях и о порядке изложения и представления результатов. В сводке статистического материала отдельные единицы статистической совокупности объединяются в группы при помощи метода группировок. Статистическая ...
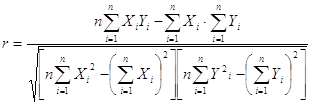
0 комментариев