Навигация
Дисперсійний аналіз та побудова статистичних графіків
15067
знаков
2
таблицы
0
изображений
Дисперсійний аналіз та побудова статистичних графіків
Дисперсійний аналіз
Характеристики варіації
В одних сукупностях індивідуальні значення ознаки щільно групуються навколо центра розподілу, в інших — значно відхиляються. Чим менші відхилення, тим однорідніша сукупність, а отже, тим більш надійні й типові характеристики центра розподілу, передусім середня величина. Вимірювання ступеня коливання ознаки, її варіації — невід'ємна складова аналізу закономірностей розподілу. Міри варіації широко використовуються у практичній діяльності: для оцінювання диференціації домашніх господарств за рівнем доходу, фінансового ризику інвестування, ритмічності роботи підприємств, сталості врожайності сільськогосподарських культур тощо.
На основі характеристик варіації оцінюється інтенсивність структурних зрушень, щільність взаємозв'язків соціально-економічних явищ, точність результатів вибіркового обстеження.
Для вимірювання та оцінювання варіації використовуються абсолютні та відносні характеристики. До абсолютних належать: варіаційний розмах, середнє лінійне та середнє квадратичне відхилення, дисперсії; відносні характеристики подаються низкою коефіцієнтів варіації, локалізації, концентрації.
Узагальнюючою характеристикою варіації є середнє відхилення:
а) лінійне
,
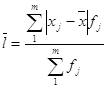б) квадратичне, або стандартне
;
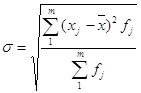в) дисперсія (середній квадрат відхилень)
.
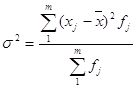Види та взаємозв'язок дисперсій
Дисперсія посідає особливе місце у статистичному аналізі соціально-економічних явищ. На відміну від інших характеристик варіації завдяки своїм математичним властивостям вона є невіддільним і важливим елементом інших статистичних методів, зокрема дисперсійного аналізу.
Для ознак метричної шкали дисперсія — це середній квадра відхилень індивідуальних значень ознаки від середньої:
.
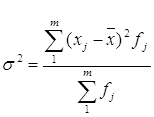Як і будь-яка середня, дисперсія має певні математичні властивості. Сформулюємо найважливіші з них.
1. Якщо всі значення варіант xj зменшити на сталу величину А, то дисперсія не зміниться:
.
2. Якщо всі значення варіант xj змінити в А раз, то дисперсія зміниться в А2 раз:
.
3. Якщо частоти замінити частками, дисперсія не зміниться. Нескладними алгебраїчними перетвореннями можна довести,
що дисперсія — це різниця квадратів 
. Якщо
,
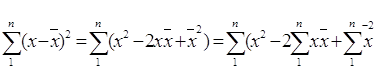то, замінивши 
і поділивши всі складові на п, дістанемо:
,
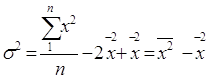де 
– квадрат середньої величини; – середній квадрат значень ознаки.
Дисперсія альтернативної ознаки обчислюється як добуток часток: 
, де d1 — частка елементів сукупності, яким властива ознака, d0 — частка решти елементів 
. Застосуємо основну формулу дисперсії до цих характеристик структури:
.
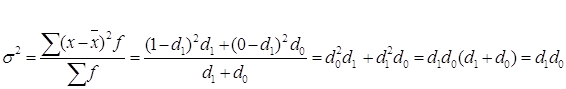Якщо, скажімо, у збиральному цеху частка висококваліфікованих робітників становить d1= 0,2, то дисперсія частки
σ2=0,2 (1-0,2)=0,16.
Дисперсія альтернативної ознаки широко використовується при проектуванні вибіркових обстежень, обробці даних соціологічних опитувань, статистичному контролі якості продукції тощо. За відсутності первинних даних про розподіл сукупності припускають, що d1=d0=0,5 і використовують максимальне значення
дисперсії σ2 =0,5·0,5=0,25.
Якщо сукупність розбито на групи за певною ознакою х, то для будь-якої іншої ознаки у можна обчислити дисперсію як у цілому по сукупності, так і в кожній групі. Центром розподілу сукупності в цілому є загальна середня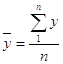 
, центром розподілу в j-й групі — групова середня 
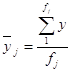. Відхилення індивідуальних значень ознаки у від загальної середньої 
можна подати як дві складові: 
. Узагальнюючими характеристиками цих відхилень є дисперсії: загальна, групова та міжгрупова.
Загальна дисперсія характеризує варіацію ознаки у навколо загальної середньої:
.
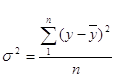Групова дисперсія характеризує варіацію відносно групової середньої:
.
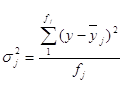Оскільки в групи об'єднуються певною мірою схожі елементи сукупності, то варіація в групах, як правило, менша, ніж у цілому по сукупності. Якщо причинні комплекси, що формують варіацію в різних групах, неоднакові, то й групові дисперсії різняться між собою.
Узагальнюючою мірою внутрішньогрупової варіації є середня з групових дисперсій:
.
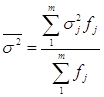Різними є й групові середні 
. Мірою варіації їх навколо загальної середньої є міжгрупова дисперсія
.
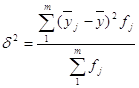Отже, загальна дисперсія складається з двох частин. Перша характеризує внутрішньогрупову, друга — міжгрупову варіацію.
Взаємозв'язок дисперсій називається правилом розкладання (декомпозиції) варіації:
.
Похожие работы
... іжності між емпіричними і теоретичними частотами розподілу не можуть бути випадковими і припущення про близькість емпіричного розподілу до нормального повинна бути спростоване. Розділ 3. Кореляційний аналіз виробництва льоноволокна Одним з найважливіших завдань статистики є вивчення об'єктивно існуючих зв'язків між явищами. При дослідженні таких зв'язків з'ясовуються причинно-наслідкові ві ...
... підприємства. На основі цього можна визначитися в можливих обсягах виробництва продукції кожного виду і з'ясувати резерви зростання її обсягів. Важливим моментом є визначення каналів реалізації кожного виду продукції птахівництва. Більш ефективною є реалізація її підприємством через фірмові магазини, ларкі та на ринках. Можлива також реалізація через оптові торговельні організації. Потрібно ...
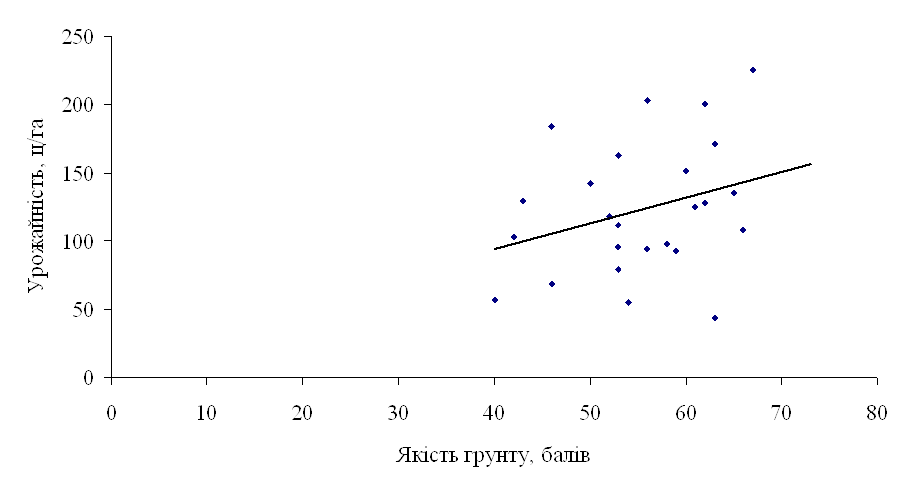
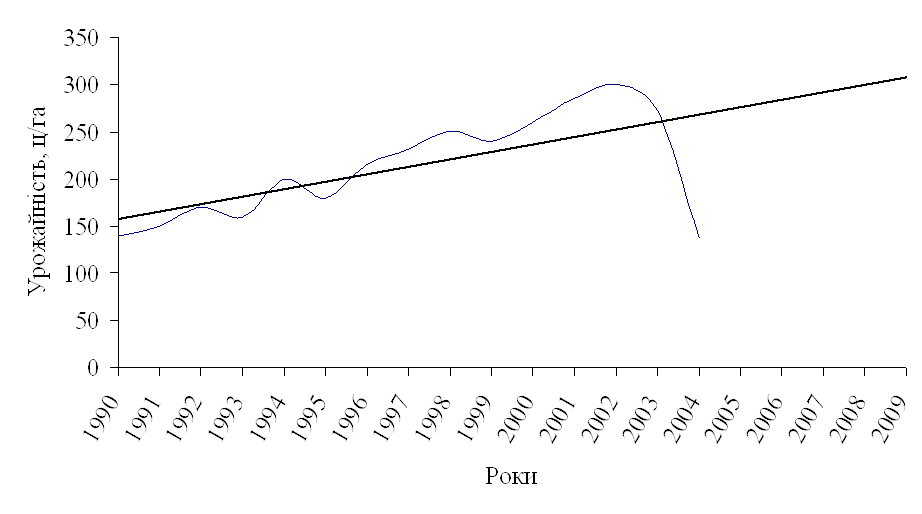
... лінію регресії (рис.4). Рис 4. Кореляційне поле залежності урожайності цукрових буряків від якості ґрунту Розділ IV. Динаміка та прогнозування урожайності цукрових буряків 4.1 Перспективи розвитку урожайності цукрових буряків в господарствах Андрушівського району Рядом динаміки називається тимчасова послідовність значень статистичних показників. Ряд динаміки складається із ...
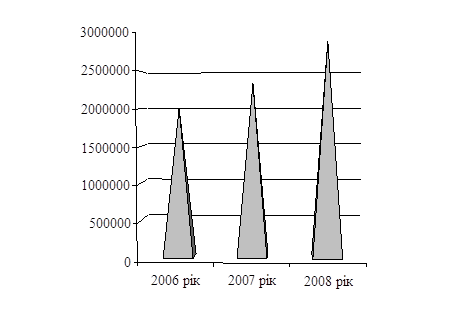
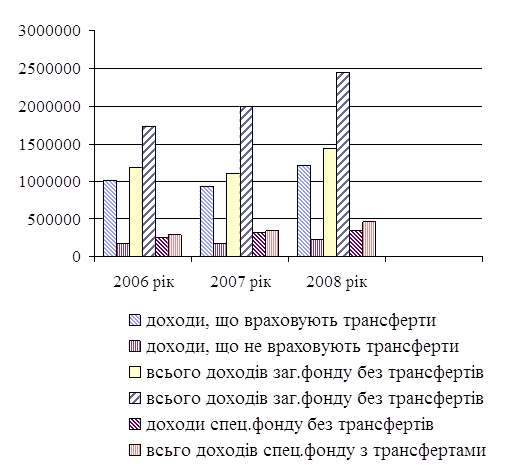
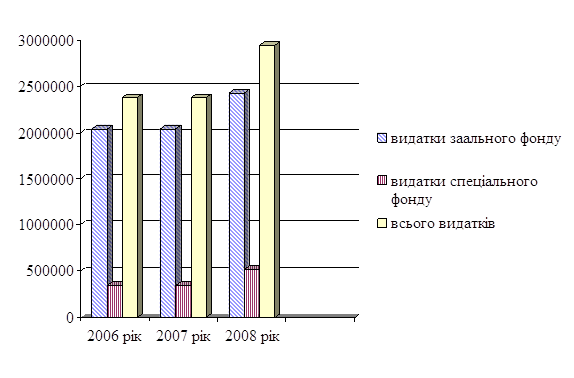
... із виконання доходної та видаткової частини бюджету. Отже, наступний розділ дипломної роботи присвятимо висвітленню характеристики і поглибленому аналізу стану даної проблеми. Розділ 2. Аналіз виконання і планування місцевих бюджетів 2.1 Аналіз виконаня місцевих бюджетів по Харківській області Місцевий бюджет виконується за розписом, який затверджується керівником місцевого фінансового ...
0 комментариев