Навигация
Сумма элементов матрицы A по любому из столбцов меньше единицы, т.е
2. Сумма элементов матрицы A по любому из столбцов меньше единицы, т.е.
![]()
![]()
Доказать это утверждение несложно.
Для любой отрасли условно чистая продукция есть величина положительная, поскольку включает в себя заработную плату, амортизацию, прибыль и т.д., т.е. Vj>0. Поэтому, используя соотношение (3.2), можно записать:
![]() из соотношения (3.3):
из соотношения (3.3): ![]()
откуда безусловно следует:
![]()
таким образом, утверждение доказано.
Можно показать, что при выполнении этих двух условий матрица B = (E - A) - 1 существует и если ее элементы неотрицательны. Говорят, что в этом случае матрица прямых затрат А является продуктивной.
Перепишем формулу (3.5):
X = BY, (3.6)
Матрица В носит название матрицы полных материальных затрат, а ее элементы bij называют коэффициентами полных материальных затрат. Коэффициент bij показывает, каков должен быть валовый выпуск i-й отрасли для того, чтобы обеспечить выпуск единицы конечного продукта j-й отрасли.
Можно показать, что
B = E + A + A2 + A3 +... (3.7)
Умножим обе части на (E - A):
B (E - A) = (E + A + A2 + A3 +. .) (E - A),
B (E - A) = E + A + A2 + A3 +. - A - A2 - A3 - ...,
B (E - A) = E,
B = E / (E - A),
B = (E - A) - 1.
Доказано.
Из соотношения (3.7) следует bij ≥ aij, ![]()
![]() Таким образом, коэффициент полных материальных затрат bij, описывающий потребность в выпуске продукции i-й отрасли в расчете на единицу конечного продукта j-й отрасли, не меньше коэффициента прямых материальных затрат aij, рассчитываемого на единицу валового выпуска.
Таким образом, коэффициент полных материальных затрат bij, описывающий потребность в выпуске продукции i-й отрасли в расчете на единицу конечного продукта j-й отрасли, не меньше коэффициента прямых материальных затрат aij, рассчитываемого на единицу валового выпуска.
Кроме того, из соотношения (3.7) для диагональных элементов матрицы B следует:
bii ≥ 1, ![]()
Взаимосвязь коэффициентов прямых и полных материальных затрат проще всего проследить на примере: пусть единицей выпуска хлебопекарной промышленности является хлеб (рисунок 3.1).
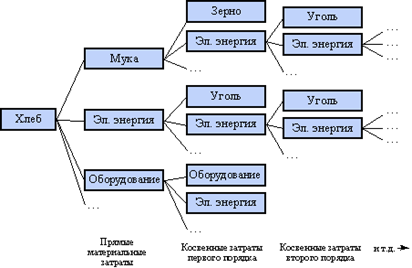
Рисунок 3.1 - Взаимосвязь коэффициентов прямых и полных материальных затрат
Полные затраты электроэнергии для нашего примера складываются из прямых затрат и косвенных затрат всех уровней. Косвенные затраты высоких уровней являются незначительными и при практических расчетах ими можно пренебречь.
3. Модель межотраслевого баланса затрат труда
Предполагается, что труд выражается в единицах труда одинаковой степени сложности. Обозначим затраты живого труда в производстве j-го продукта через Lj, объем выпущенной продукции, как и прежде, Xj. Тогда коэффициент прямых затрат труда:
![]()
Определим полные затраты труда, как сумму прямых затрат живого труда и затрат овеществленного труда, перенесенного на продукт через израсходованные средства производства.
Формирование полных затрат труда в модели происходит по схеме, представленной на рисунке 3.2
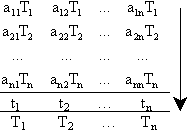
Рисунок 3.2 - Порядок формирования полных затрат труда
где Tj - полные затраты труда на единицу j-го продукта; tj - прямые затраты труда на единицу j-го продукта; aijTi - затраты овеществленного труда, перенесенного на j-й продукт через i-е средство производства.
Таким образом:
![]()
![]()
Иначе, если известны коэффициенты полных материальных затрат bij, можно записать:
![]()
![]()
Более компактно соотношение можно записать в матричном виде:
T = tB,
где T = (T1, T2,..., Tn) - вектор-строка коэффициентов полных затрат труда;
t = (t1, t2,..., tn) - вектор-строка коэффициентов прямых затрат труда.
Аналогично трудовым затратам в межотраслевой модели могут быть учтены показатели фондоемкости изделий.
Василий Леонтьев, характеризуя значение балансовых моделей, писал: "Чтобы прогнозировать развитие экономики, нужен системный подход. Экономика каждой страны - это большая система, в которой много различных отраслей, и каждая из них что-то производит - промышленную продукцию, услуги и т.д., которые предлагаются другим отраслям. Каждое звено, компонент системы может существовать только потому, что получает что-то от других. Для производства каждого вида продукции нужно напрямую использовать большое количество других товаров, а еще больше - опосредованно.
Мы изучаем одну страну, беря в расчет 600-700 отдельных отраслей, японцы доходят до 2000".
4. Пример расчета межотраслевого баланса
Рассмотрим 2 отрасли промышленности: производство угля и стали. Уголь требуется для производства стали и некоторое количество стали в виде инструментов требуется для добычи угля. Предположим, что условия таковы: для производства 1 т. стали нужно 3 т. угля, а для 1 т. угля - 0,1 т. стали.
| Отрасль | Уголь | Сталь |
| Уголь | 0 | 3 |
| Сталь | 0.1 | 0 |
Мы хотим, чтобы чистый выпуск угольной промышленности был ![]() тонн угля, а стальной промышленность -
тонн угля, а стальной промышленность - ![]() тонн стали. Если каждая из них будет производить лишь
тонн стали. Если каждая из них будет производить лишь ![]() и
и ![]() тонн, то часть продукции будет использоваться в другой отрасли. Для производства
тонн, то часть продукции будет использоваться в другой отрасли. Для производства ![]() тонн стали требуется
тонн стали требуется ![]() тонн угля, а для производства
тонн угля, а для производства ![]() тонн угля нужно
тонн угля нужно ![]() тонн стали. Чистый выход будет равен:
тонн стали. Чистый выход будет равен: ![]() тонн угля и
тонн угля и ![]() тонн стали. Нам нужно дополнительно производить уголь и сталь, чтобы использовать их в другой отрасли. Обозначим x1 - количество угля, x2 - количество стали. Валовый выпуск каждой продукции найдем из системы уравнений:
тонн стали. Нам нужно дополнительно производить уголь и сталь, чтобы использовать их в другой отрасли. Обозначим x1 - количество угля, x2 - количество стали. Валовый выпуск каждой продукции найдем из системы уравнений:
![]()
Решение: (500000; 100000). Для систематического решения задач расчета межотраслевого баланса находят, сколько угля и стали требуется для выпуска 1 т. каждого продукта.
![]()
x1 = 1,42857 и x2 = 0,14286. Чтобы найти, сколько угля и стали нужно для чистого выпуска ![]() т. угля, нужно умножить эти цифры на
т. угля, нужно умножить эти цифры на ![]() . Получим: (285714; 28571). Аналогично составляем уравнения для получения количества угля и стали для выпуска 1 т. стали:
. Получим: (285714; 28571). Аналогично составляем уравнения для получения количества угля и стали для выпуска 1 т. стали:
![]()
x1 = 4.28571 и x2 = 1.42857. Для чистого выпуска ![]() т. стали нужно: (214286; 71429). Валовый выпуск для производства
т. стали нужно: (214286; 71429). Валовый выпуск для производства ![]() тонн угля и
тонн угля и ![]() тонн стали: (285714 + 214286; 28571 + 71429) = (500000; 100000).
тонн стали: (285714 + 214286; 28571 + 71429) = (500000; 100000).
Список использованных источников
1. Герасенко В.П. Прогностические методы управления рыночной экономикой. Учебное пособие. - Гомель, 1997
2. Горелов С.А. Математические методы в прогнозировании. - М.: Прогресс, 2003
3. Карасев А.И. Математические модели в планировании. - М., 2004
4. Орешин В.П. Государственное регулирование национальной экономики. - М., 1999
5. Основы экономического и социального прогнозирования. / Под ред. Н.А. Мосина - М.: Высшая школа, 2005
6. Прогнозирование и планирование экономики. / Под ред. В.И. Борисевича, Г.А. Кандауровой. - Мн., 2000
7. Цыгичко В.А. Основы прогнозирования систем. - М.: Финансы и статистика, 2006.
8. Леонтьев В.В. Экономические эссе. Теории, исследования, факты и политика: Пер. с англ. / В.В. Леонтьев. - М.: Политиздат, 1990. - 415 с.
9. М.Р. Ефремова, Е.В. Петрова "Общая теория статистики": учебник, 2007 г.
10. Сироткина Т.С., Каманина А.М. Основы теории статистики: учебное пособие. - М.: АО "Финстатинформ", 1995.
Похожие работы
... результатов нерыночной деятельности и свободного времени.2. Модель межотраслевого баланса как инструмент исследования и прогнозирования 2.1 Методология построения межотраслевого баланса в системе национальных счетов Межотраслевой баланс в концепции системы национальных счетов (МОБ СНС) – важный вид балансовых построений. Являясь дальнейшим развитием и детализацией счета производства и ...
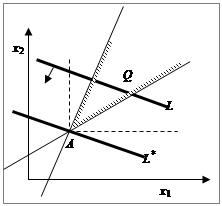
... задачи имеет место при любых положительных значениях tjи . Оно означает, что суммарная оценка всей конечной продукции равна сумме трудовых затрат в народном хозяйстве. Оптимизационная модель межотраслевого баланса продукции и производственных мощностей. При анализе возможностей использования модели межотраслевого баланса в планировании отмечалось, что при краткосрочном планировании ...
... металлов; - слабо развито производство товаров и услуг, которое способно составить конкуренцию на международных и мировых рынках. 3. Анализ достоинств и недостатков "системы национальных счетов" и "межотраслевого баланса В. Леонтьева" 3.1 Достоинства и недостатки СНС 1. Одним из основных достоинств СНС, является единство системы статистических показателей экономической деятельности и ее ...
... Коэффициенты полных затрат используются для расчета валовой продукции по каждой отрасли путем их умножения на объем конечного продукта (конечного использования ВНП). 2. Прогнозирование и планирование трудовых ресурсов и занятости Трудовые ресурсы - это часть населения, которая в силу совокупности физических способностей, специальных знаний и опыта может участвовать в создании материальных ...
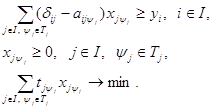
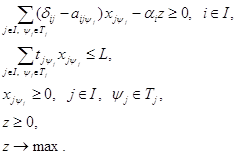
0 комментариев