Навигация
Расчет моды и медианы в интервальном вариационном ряду
3. Расчет моды и медианы в интервальном вариационном ряду
Описательный характер моды и медианы связан с тем, что в них не погашаются индивидуальные отклонения. Они всегда соответствуют определенной варианте. Поэтому мода и медиана не требуют для своего нахождения расчетов, если известны все значения признака. Однако в интервальном вариационном ряду для нахождения приближенного значения моды и медианы в пределах определенного интервала прибегают к расчетам.
Для расчета определенного значения модальной величины признака, заключенного в интервале, применяют формулу:
Мо = ХМо + iМо *(fМо – fМо-1)/((fМо – fМо-1) + (fМо – fМо+1)),
Где ХМо – минимальная граница модального интервала;
iМо – величина модального интервала;
fМо – частота модального интервала;
fМо-1 – частота интервала, предшествующего модальному;
fМо+1 – частота интервала, следующего за модальным.
Покажем расчет моды на примере, приведенном в таблице 2.
Таблица 2. Распределение рабочих предприятия по выполнению норм выработки
| Выполнение норм выработки, % | Численность рабочих |
| 90 – 95 | 6 |
| 95 – 100 | 12 |
| 100 -105 | 104 |
| 105 – 110 | 98 |
| 110 -115 | 40 |
| 115 и более | 20 |
| Итого | 280 |
Чтобы найти моду, первоначально определим модальный интервал данного ряда. Из примера видно, что наибольшая частота соответствует интервалу, где варианта лежит в пределах от 100 до 105. Это и есть модальный интервал. Величина модального интервала равна 5.
Подставляя числовые значения из таблицы 2. в указанную выше формулу, получим:
Мо = 100 + 5 * (104 -12)/((104 – 12) + (104 – 98)) = 108,8
Смысл этой формулы заключается в следующем: величину той части модального интервала, которую нужно добавить к его минимальной границе, определяют в зависимости от величины частот предшествующего и последующего интервалов. В данном случае к 100 прибавляем 8,8, т.е. больше половины интервала, потому что частота предшествующего интервала меньше частоты последующего интервала.
Исчислим теперь медиану. Для нахождения медианы в интервальном вариационном ряду определяем сначала интервал, в котором она находится (медианный интервал). Таким интервалом будет такой, комулятивная частота которого равна или превышает половину суммы частот. Комулятивные частоты образуются путем постепенного суммирования частот, начиная от интервала с наименьшим значением признака. Половина суммы частот у нас равна 250 (500:2). Следовательно, согласно таблицы 3. медианным интервалом будет интервал со значением заработной платы от 350000 руб. до 400000 руб.
Таблица 3. Расчет медианы в интервальном вариационном ряду
| Заработная плата, тыс. руб. | Частоты | Комулятивные частоты |
| 200 – 250 | 10 | 10 |
| 250 – 300 | 50 | 60 |
| 300 – 350 | 100 | 160 |
| 350 – 400 | 115 | 275 |
| 400 – 450 | 180 | 455 |
| 450 – 500 | 45 | 500 |
| Сумма | 500 | - |
До этого интервала сумма накопленных частот составила 160. Следовательно, чтобы получить значение медианы, необходимо прибавить еще 90 единиц (250 – 160).
При определении значения медианы предполагают, что значение единиц в границах интервала распределяется равномерно. Следовательно, если 115 единиц, находящихся в этом интервале, распределяются равномерно в интервале, равном 50, то 90 единицам будет соответствовать следующая его величина:
50 * 90/115 = 39,1
Прибавив полученную величину к минимальной границе медианного интервала, получим искомое значение медианы:
Ме = 350 +39,1 = 389,1 тыс. руб.
Формула исчисления медианы для интервального вариационного ряда имеет следующий вид:
Ме = ХМе + iМе * (∑f/2 – SМе-1)/fМе,
Где ХМе – начальное значение медианного интервала;
iМе – величина медианного интервала;
∑f – сумма частот ряда (численность ряда);
SМе-1 – сумма накопленных частот в интервалах, предшествующих медианному;
fМе – частота медианного интервала.
Подставляя в эту формулу значения из примера, приведенного выше, получим значение медианы:
Ме = 350 + 50 * (500/2 – 160)/115 = 389,1 тыс. руб.
Следовательно, в наших примерах мода равна 108,8, а медиана – 389,1.
4. Квартили и децили – дополнительные характеристики вариационного ряда
Дополнительно к медиане для характеристики вариационного ряда исчисляют квартили, которые делят ряд по сумме частот на четыре равные части, и децили, которые делят ряд на десять равных частей. Второй квартиль равен медиане, а первый – Q1 и третий – Q3 исчисляют аналогично расчету медианы, только вместо медианного интервала берется для первого квартиля интервал, в котором находится варианта, отсекающая ¼ численности частот, а для третьего квартиля – варианта, отсекающая ¾ численности частот. Исчислим для нашего примера первый и третий квартили:
Q1 = XQ1 +iQ1 * (∑f/4 – SQ1-1)/fQ1,
Q1 = 300 + 50 * (125–60)/100 = 332,5
Для расчета первого квартиля находим ¼ всех частот: ∑f/4 составит 125 (500/4). Из таблицы 3 видно, что 125-я варианта находится в интервале 300 – 350.
Следовательно, XQ1 = 300. Сумма накопленных частот до этого интервала равна 60 (SQ1-1), частота этого интервала – 100. Расчет дает значение первого квартиля 332,5 тыс. руб. Это означает, что у трех четвертей всех рабочих заработная плата составляет 332,5 тыс. руб. и выше.
Рассчитаем третий квартиль. Три четверти численности частот (3/4 ∑f) составит 375 = 500*3/ 4. 375-я варианта находится в интервале 400 – 450. Следовательно:
Q3 = XQ3 + iQ3 * (3/4∑f – SQ3-1)/fQ3,
Q3 = 400 + 50 *(375 – 275)/180 = 427,75
Третий квартиль составляет 427,75 тыс. руб. Следовательно, заработная плата каждого четвертого работника превышает 427,75 тыс. руб.
Заключение
Исходя из контрольной работы, можно сделать вывод, что средние величины и их разновидности в статистике играют большую роль. Средние показатели широко применяются в анализе, так как именно в них находят свое проявление закономерности массовых явлений и процессов как во времени, так и в пространстве. Так, например, закономерность повышения производительности труда находит свое выражение в статистических показателях роста средней выработки на одного работающего в промышленности, закономерность неуклонного роста уровня благосостояния населения проявляется в статистических показателях увеличения средних доходов рабочих и служащих и т.д.
Широкое применение имеют такие описательные характеристики распределения варьирующего признака как мода и медиана. Они являются конкретными характеристиками, их значение имеет какая-либо конкретная варианта в вариационном ряду.
Так, чтобы охарактеризовать наиболее часто встречающуюся величину признака, применяют моду, а чтоб показать количественную границу значения варьирующего признака, которую достигла половина членов совокупности – медиану.
Таким образом, средние величины помогают изучать закономерности развития промышленности, конкретной отрасли, общества и страны в целом.
Похожие работы
... называется группа упорядоченных по величине значений признака, заменяемая в процессе расчетов средним значением. 2. Методы вторичной статистической обработки результатов эксперимента С помощью вторичных методов статистической обработки экспериментальных данных непосредственно проверяются, доказываются или опровергаются гипотезы, связанные с экспериментом. Эти методы, как правило, сложнее, ...
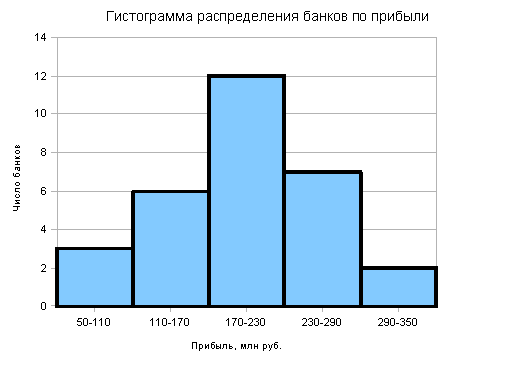
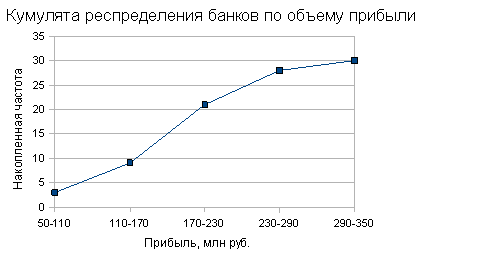
... 6 1 50-110 3 10 3 10,0 2 110-170 6 20 9 30,0 3 170-230 12 40 21 70,0 4 230-290 7 23,3 28 93,3 5 290-350 2 6,7 30 100,0 Итого 30 100,0 Вывод. Анализ статистического ряда распределения изучаемой совокупности банков показывает, что распределение банков по объему прибыли не является равномерным: преобладают банки с прибылью от 170 млн руб. до 230 ...
... 48 103,2-120,0 33 41 58 47 Рассчитаем относительный показатель интенсивности (ОПИ) по формуле: Полученные данные разместим в таблице 9. Таблица 9. Расчет относительных показателей интенсивности. Группы предприятий по среднегодовой заработной плате Число предприятий в группе Среднесписочная численность работников, чел. Фонд заработной платы, млн. руб. Относительный показатель ...
... анализа общее, в свою очередь, объединяет, т.е. синтезирует, обобщаемые явления. Сравнение как рабочий прием познания того или иного явления, понятия, соотношения применяется во многих учебных дисциплинах. В экономическом анализе способ сравнения считается одним из важнейших: с него и начинается анализ. Существует несколько форм сравнения с планом, сравнение с прошлым, сравнение с лучшим, ...
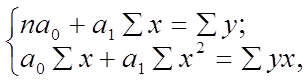
0 комментариев