ЗАДАНИЕ 1
Вы - предприниматель. Основной вид Вашей деятельности - торговля молочными продуктами. В таблице, приведены данные о количестве продаж кефира (в тыс. шт. упаковок) в четырех городах Крыма. Требуется проверить гипотезу, что среднее количество продаж упаковок кефира одинаково во всех четырех городах. В случае отвержения этой гипотезы определить в каких городах количество продаж значимо отличается от остальных и в каких городах количество продаж можно считать одинаковым. В табл.1.1 приведены варианты заданий.
Таблица 1.1 Варианты заданий
| Вариант 6 | |
| Севастополь | 4.8 5.6 4.8 5.2 4.8 5.6 6.4 6.8 5.6 5.6 5.2 5.2 |
| Керчь | 1.6 1.6 1.3 1.5 1.7 1.7 1.6 1.6 1.5 1.4 1.5 1.3 |
| Ялта | 1.0 1.0 1.2 0.8 0.8 1.0 1.2 1.3 1.1 0.9 0.9 0.8 |
| Феодосия | 0.78 0.78 0.91 0.78 1.04 1.04 1.17 1.17 1.04 0.91 0.78 0.78 |
1. Если значения выходной переменной разбито на группы и каждая группа записана в отдельном столбце (как в нашем случае), то для проведения однофакторного дисперсионного анализа необходимо выбрать из меню Stat - ANOVA - Oneway [Unstacked] и заполнить диалоговое окно Responses [in separate columns] = S K F Y, нажимаем ОК и получим следующую таблицу (см Табл. 1.2)
Таблица 1.2 полученный результат
One-Way Analysis of Variance
Analysis of Variance
Source DF SS MS F P
Factor 3 170.059 56.686 493.52 0.000
Error 44 5.054 0.115
Total 47 175.113
Individual 95% CIs For Mean
Based on Pooled StDev
Level N Mean StDev ------+---------+---------+---------+
S 12 5.4667 0.6228 (*-)
K 12 1.5250 0.1357 (*)
F 12 0.9317 0.1551 (*-)
Y 12 1.0000 0.1706 (-*)
------+---------+---------+---------+
Pooled StDev = 0.3389 1.5 3.0 4.5 6.0
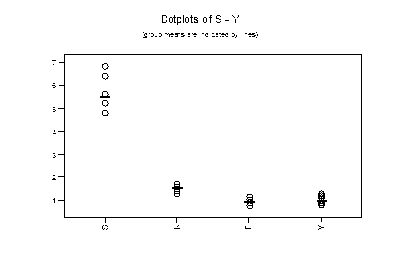
Из полученных данных мы можем сделать вывод, что большинство молочной продукции продается в S (Севастополе). Но можно считать, что примерно одинаково количество продаж приходится на Керчь, Феодосию и Ялту, со значительной разницей по сравнению с Севастополем.
ЗАДАНИЕ 2
В таблице приведены данные опроса 32 человек. Опрашиваемые были выбраны случайным образом из групп людей, которые формировались так, чтобы результаты опроса были сбалансированы по всем уровням факторов.
Таблица 2.1 Результаты опроса
| Образование | Сфера деятельн. | Пол | Положение | Доход | Расход |
| X1 | X2 | X3 | X4 | Y1 | Y2 |
| Экономич. | Финансы | Муж. | Руковод. | 852 | 650 |
| Экономич. | Финансы | Жен. | Руковод. | 750 | 700 |
| Экономич. | Производ. | Муж. | Руковод. | 210 | 140 |
| Экономич. | Производ. | Жен. | Руковод. | 180 | 160 |
| Экономич. | Сельск,х. | Муж. | Работник | 120 | 80 |
| Экономич. | Сельск,х. | Жен. | Работник | 130 | 120 |
| Экономич. | Образов. | Муж. | Работник | 210 | 180 |
| Экономич. | Образов. | Жен. | Работник | 190 | 170 |
| Технич. | Финансы | Муж. | Работник | 320 | 240 |
| Технич. | Финансы | Жен. | Работник | 240 | 220 |
| Технич. | Производ. | Муж. | Работник | 230 | 180 |
| Технич. | Производ. | Жен. | Работник | 140 | 130 |
| Технич. | Сельск,х. | Муж. | Руковод. | 350 | 300 |
| Технич. | Сельск,х. | Жен. | Руковод. | 360 | 320 |
| Технич. | Образов. | Муж. | Руковод. | 310 | 250 |
| Технич. | Образов. | Жен. | Руковод. | 310 | 300 |
| Медицин, | Финансы | Муж. | Руковод. | 540 | 450 |
| Медицин, | Финансы | Жен. | Руковод. | 450 | 420 |
| Медицин, | Производ. | Муж. | Руковод. | 310 | 210 |
| Медицин, | Производ. | Жен. | Руковод. | 405 | 380 |
| Медицин, | Сельск,х. | Муж. | Работник | 110 | 100 |
| Медицин, | Сельск,х. | Жен. | Работник | 120 | 110 |
| Медицин, | Образов. | Муж. | Работник | 210 | 180 |
| Медицин, | Образов. | Жен. | Работник | 180 | 170 |
| Гуманит. | Финансы | Муж. | Работник | 230 | 160 |
| Гуманит. | Финансы | Жен. | Работник | 240 | 220 |
| Гуманит. | Производ. | Муж. | Работник | 120 | 110 |
| Гуманит. | Производ. | Жен. | Работник | 125 | 120 |
| Гуманит. | Сельск,х. | Муж. | Руковод. | 280 | 180 |
| Гуманит. | Сельск,х. | Жен. | Руковод. | 300 | 280 |
| Гуманит. | Образов. | Муж. | Руковод. | 240 | 230 |
| Гуманит. | Образов. | Жен. | Руковод. | 230 | 200 |
Требуется методом двухфакторного дисперсионного анализа оценить степень влияния изучаемых факторов на результирующий экономический показатель. Первоначально оценить модель без взаимодействия факторов, затем с взаимодействием. Сравнить результаты. Сделать выводы.
Варианты заданий
| Вариант | Первый фактор | Второй фактор | Отклик | Вариант | Первый фактор | Второй фактор | Отклик |
| 1 | X1 | X2 | Y1 | 7 | X1 | X2 | Y2 |
| 2 | X1 | X3 | Y1 | 8 | X1 | X3 | Y2 |
| 3 | X1 | X4 | Y1 | 9 | X1 | X4 | Y2 |
| 4 | X2 | X3 | Y1 | 10 | X2 | X3 | Y2 |
| 5 | X2 | X4 | Y1 | 11 | X2 | X4 | Y2 |
| 6 | X3 | X4 | Y1 | 12 | X3 | X4 | Y2 |
Произведем расчет в системе MINITAB. Определим, как влияет пол, должность и их взаимодействие на доход. Заполним таблицу данными согласно заданию. Затем Путь: ANOVA - Balanced ANOVA и заполним диалоговое окно следующим образом:
Responses: Y1
Model: X3 X4 X3*X.
Получим следующие данные
Factor Type Levels Values
X3 fixed 2 Муж. Жен.
X4 fixed 2 Руковод. Работник
Analysis of Variance for Y1
Source DF SS MS F P
X3 1 2665 2665 0.13 0.724
X4 1 312445 312445 14.88 0.001
X3*X4 1 190 190 0.01 0.925
Error 28 587802 20993
Total 31 903102
Исходя из полученных результатов, можно сделать вывод, что на доход существенно влияет положение, а не пол. Мужчины руководители имеют больший доход, чем женщины, а женщины рабочие в свою очередь имеют больший доход, нежели мужчины.
Похожие работы
... на задний план традиционными постановками. Несколько лет назад при описании современного этапа развития статистических методов нами были выделены [29] пять актуальных направлений, в которых развивается современная прикладная статистика, т.е. пять "точек роста": непараметрика, робастность, бутстреп, интервальная статистика, статистика объектов нечисловой природы. Обсудим их. 5. ...
... економічної діяльності та ЄДРПОУ. Статистичний звіт — це документ, який вміщує систему показників діяльності суб’єктів господарювання. Зміст звіту, форма та термін подання в органи державної статистики затверджуються Держкомстатом України. Крім загально державної статистичної звітності існує відомча звітність, яка розробляється міністерствами та відомствами для внутрішніх управлінських потреб. ...
... гипотезу. Вроде бы это надо делать так: Теперь результаты наблюдений над выручкой G можно представить в виде четырех наблюдений над U: –11,+1,+3,+7. Теория математической статистики предлагает следующий, т.н. биномиальный критерий проверки гипотез в подобных ситуациях. Предполагается, что распределение вероятностей наблюдаемой величины U симметрично относительно значения математического ...
... анализы являются частными случаями общей схемы регрессионного анализа в пространстве произвольной природы [110]. Поскольку структура модели - объект нечисловой природы, то ее оценивание, в частности, оценивание степени полинома в регрессии, также относится к статистике объектов нечисловой природы (см. например, [111, 112]). Если учесть, что результаты измерения всегда имеют погрешность, т. е. ...
0 комментариев