Навигация
Современная прикладная статистика
Дается критический анализ современного состояния прикладной статистики. Обсуждаются тенденции развития статистических методов.
1. Что дает прикладная статистика народному хозяйству?
Так называлась статья [1], в которой приводились многочисленные примеры успешного использования методов прикладной математической статистики. при решении практических задач. Перечень примеров можно продолжать практически безгранично. Из работ 1997 г. достаточно сослаться на обобщающую статью В.Г.Горского [2], на диссертацию А.Н.Гуды [3]. По данным Института информации Гарфилда (США) каждая из основополагающих книг В.В.Налимова [4,5] цитировалась не менее 1000 раз (см. также монографию [6, с.270,274,373]). В любом номере журнала "Заводская лаборатория" есть работы, в которых те или иные методы прикладной статистики применяются для решения прикладных задач. Не раз публиковались в нашем журнале и обобщающие статьи [7-9].
Поэтому бесспорно совершенно, что методы прикладной статистики успешно применяются в различных отраслях народного хозяйства, практически во всех областях науки. Согласно докладу [10, с.157-158] в 1988 г. затраты в СССР на статистический анализ данных оценивались в 2 миллиарда рублей ежегодно.
Большая практическая значимость прикладной статистики оправдывает целесообразность проведения работ по ее методологии, в которых эта область научной и прикладной деятельности рассматривалась бы как целое, "с высоты птичьего полета". Чтобы иметь возможность обсуждения тенденций развития статистических методов, кратко рассмотрим их историю.
2. Об истории прикладной статистики
Типовые примеры раннего этапа применения статистических методов описаны в Ветхом Завете (см., например, Книгу Чисел). С математической точки зрения они сводились к подсчетам числа попаданий значений наблюдаемых признаков в определенные градации. В дальнейшем результаты стали представлять в виде таблиц и диаграмм, как это и сейчас делает Госкомстат РФ. Надо признать, что по сравнению с Ветхим Заветом есть прогресс - в Библии не было таблиц. Однако нет продвижения по сравнению с работами российских статистиков конца девятнадцатого - начала двадцатого века (типовой монографией тех времен можно считать книгу [11], которая в настоящее время еще легко доступна).
Сразу после возникновения теории вероятностей (Паскаль, Ферма, 17 век) вероятностные модели стали использоваться при обработке статистических данных. Например, изучалась частота рождения мальчиков и девочек, было установлено отличие вероятности рождения мальчика от 0.5, анализировались причины того, что в парижских приютах эта вероятность не та, что в самом Париже, и т.д. Имеется достаточно много публикаций по истории теории вероятностей, однако в некоторых из них имеются неточные утверждения, что заставило академика Украинской АН Б.В.Гнеденко включить в последнее издание своего курса [12] главу по истории математики случайного.
В 1794 г. (по другим данным - в 1795 г.) К.Гаусс разработал метод наименьших квадратов, один из наиболее популярных ныне статистических методов, и применил его при расчете орбиты астероида Церера - для борьбы с ошибками астрономических наблюдений [13]. В 19 веке заметный вклад в развитие практической статистики внес бельгиец Кетле, на основе анализа большого числа реальных данных показавший устойчивость относительных статистических показателей, таких, как доля самоубийств среди всех смертей [14]. Интересно, что основные идеи статистического приемочного контроля и сертификации продукции обсуждались академиком Буняковским и применялись в российской армии еще в середине 19 в.[15]. Статистические методы управления качеством, сертификации и классификации продукции сейчас весьма актуальны [16].
Современный этап развития прикладной статистики можно отсчитывать с 1900 г., когда англичанин К.Пирсон основан журнал "Biometrika". Первая треть ХХ в. прошла под знаком параметрической статистики. Изучались методы, основанные на анализе данных из параметрических семейств распределений, описываемых кривыми семейства Пирсона. Наиболее популярным было нормальное (гауссово) распределение. Для проверки гипотез использовались критерии Пирсона, Стьюдента, Фишера. Были предложены метод максимального правдоподобия, дисперсионный анализ, сформулированы основные идеи планирования эксперимента.
Разработанную в первой трети ХХ в. теорию будем называть параметрической статистикой, поскольку ее основной объект изучения - это выборки из распределений, описываемых одним или небольшим числом параметров. Наиболее общим является семейство кривых Пирсона, задаваемых четырьмя параметрами. Как правило, нельзя указать каких-либо веских причин, по которым конкретное распределение результатов наблюдений должно входить в то или иное параметрическое семейство. Исключения хорошо известны: если вероятностная модель предусматривает суммирование независимых случайных величин, то сумму естественно описывать нормальным распределением; если же в модели рассматривается произведение таких величин, то итог, видимо, приближается логарифмически нормальным распределением, и т.д. Однако в подавляющем большинстве реальных ситуаций подобных моделей нет, и приближение реального распределения с помощью кривых из семейства Пирсона или его подсемейств - чисто формальная операция.
Именно из таких соображений критиковал параметрическую статистику академик С.Н.Бернштейн в 1927 г. в своем докладе на Всероссийском съезде математиков [17]. Однако эта теория, к сожалению, до сих пор остается основой преподавания статистических методов и продолжает использоваться основной массой прикладников, остающихся далекими от новых веяний в статистике. Почему так происходит? Чтобы попытаться ответить на этот вопрос, обратимся к наукометрии.
Похожие работы
... ПО “Уралмаш”, “АвтоВАЗ”, МИИТ, Казахского политехнического института, Донецкого государственного университета и многих других. Затем Институт в качестве Лаборатории эконометрических исследований разрабатывал эконометрические методы анализа нечисловых данных, а также процедуры расчета и прогнозирования индекса инфляции и валового внутреннего продукта. Институт высоких статистических технологий и ...
... математическая лучше всего представлена в [2,4]. По историческим причинам основные российские работы публикуются в [3]. Обзор современного состояния статистики математической дан в [6]. Статистика объектов нечисловой природы - раздел математической статистики, в котором статистическими данными являются объекты нечисловой природы, т.е. элементы множеств, не являющихся линейными пространствами. ...
... знаниях. Целью прогнозирования является минимизация погрешности прогностических оценок. Очевидно, что научно обоснованные и планомерно разрабатываемые прогнозы являются более точными и эффективными (как основа принятия решений), чем случайные и интуитивные прогнозы. Известны различные методы прогнозирования: экспертные методы; метод анализа "индекса деловой активности"; статистические методы ...
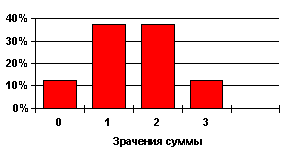
... гипотезу. Вроде бы это надо делать так: Теперь результаты наблюдений над выручкой G можно представить в виде четырех наблюдений над U: –11,+1,+3,+7. Теория математической статистики предлагает следующий, т.н. биномиальный критерий проверки гипотез в подобных ситуациях. Предполагается, что распределение вероятностей наблюдаемой величины U симметрично относительно значения математического ...


0 комментариев