Навигация
Теоретические основы математических и инструментальных методов экономики
К экономическим задачам оптимизационного типа относятся задачи, в которых требуется найти наилучшее или оптимальное решение при заданных условиях производства. Такие задачи называются задачами на максимум или минимум. Особенностью задач оптимизационного типа является многовариантность их решений, обусловленная следующими причинами: взаимозаменяемостью ресурсов; взаимозаменяемостью готовых видов продукции; существованием альтернативных технологий производства; неодинаковостью технико-экономических показателей даже однотипных хозяйственных субъектов.
Возможны два подхода к постановке оптимизационных задач: при первом подходе требуется получить максимальные конечные результаты при заданных условиях производства; при втором подходе требуется получить заданные конечные результаты при минимальных затратах ресурсов.
Математический инструментарий, позволяющий решать экономические задачи оптимального типа, называется программированием. Различают линейное и нелинейное программирование.
На практике наибольшее распространение получило линейное программирование.
Методы линейного программирования в математике известны под названием общей задачи линейного программирования.
Аналитическая формулировка общей задачи линейного программирования
Общая задача линейного программирования формулируется следующим образом:
Найти решение {Х1,Х2,….Хn}, позволяющее максимизировать или минимизировать целевую функцию
F = C1X1+C2X2+…+ CnXn
при условиях
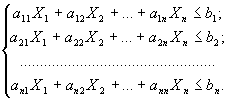
Х1≥0; Х2≥0; …; Хn≥0.
Это развернутая запись общей задачи линейного программирования.
Сокращенная запись этой модели имеет вид:
Найти решение {Xj}, позволяющее максимизировать (минимизировать) функцию
![]()
при условиях
 , i = 1,2,…,n;
, i = 1,2,…,n;
Xj ≥ 0, j = 1,2,…,n.
Вышеприведенные записи общей задачи линейного программирования называют аналитической формой записи.
Любое решение, удовлетворяющее условиям, называется допустимым решением. Допустимое решение систем неравенств, удовлетворяющее целевой функции, называется оптимальным решением. Такое решение единственно при заданных условиях.
Матричная форма записи общей задачи линейного программирования
![]()
при ограничениях AX≤B
X≥0,
где С = (с1, с2,…, сn);
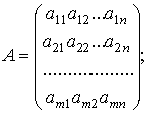
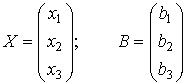
где С – матрица-строка
А – матрица системы
Х – матрица-столбец переменных
В – матрица-столбец свободных членов
Векторная форма записи общей задачи линейного программирования
F = CX → max (min)
при ограничениях
![]()
Х≥0,
где СХ – скалярное произведение векторов
С = (С1, С2, …, Сn) и Х = (х1, х2, …, хn),
векторы
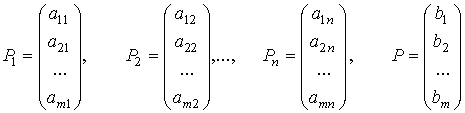
состоят соответственно из коэффициентов при переменных и свободных членов.
(про функционал)
В общем случае задача оптимизации формулируется как задача отыскания max или min значения I(v) для ![]() .
.
Под решением такой задачи понимается такое ![]() , что для остальных элементов
, что для остальных элементов ![]() выполняется неравенство
выполняется неравенство ![]() или
или ![]() в зависимости от требований задачи.
в зависимости от требований задачи.
При этом:
v – некоторая функция
I(v) – функционал вида 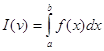
Многокритериальная оптимизация представляет собой минимизацию некого вектора целей F(x), на которой могут быть наложены дополнительные ограничения или предельные значения:
|
| (3-47) |
Отметим, что поскольку F(x) является неким вектором, то любые компоненты F(x) являюся конкурирующими и отсутсвует некое единое решение поставленной задачи. Взамен этого, для описания характеристик целей вводится концепция множества точек неулучшаемых решений [41] (так называемая оптимальность по Паретто [4],[6]). Неухудшаемое решение есть такое решение, в котором улучшение в одной из целей приводит к некому ослаблению другой. Для более точной формулировки данной концепции рассмотрим некую область допустимых решений ![]() в параметрическом пространстве
в параметрическом пространстве ![]() , которое удовлетворяет всем принятым ограничениям, т.е.
, которое удовлетворяет всем принятым ограничениям, т.е.
|
| (3-48) |
при ограничениях
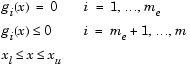
Отсюда возможно определить соответствующую область допустимых решений для пространства целевых функций ![]() .
.
|
| (3-49) |
Точка неулучшаемого решения может быть определена как:
Определение. Точка ![]() является неулучшаемым решением, если для некоторой окрестности
является неулучшаемым решением, если для некоторой окрестности ![]() нет некого
нет некого ![]() такого, что
такого, что ![]() и
и
|
|
Стратегия взвешенных сумм
Данная стратегия взвешенных сумм преобразует многокритериальную задачу минимизации вектора ![]() в некую скалярную задачу путем построения неких взвешенных сумм для всех выбранных объектов.
в некую скалярную задачу путем построения неких взвешенных сумм для всех выбранных объектов.
|
| (3-51) |
Далее уже к данной задаче оптимизации уже может быть применен стандартный алгоритм оптимизации без наличия ограничений. В этом случае рассматриваются взвешенные коэффициенты для каждой из выбранных целей. Взвешенные коэффициенты необязательно должны напрямую соответствовать относительной значимости соответствующей цели или принимать во внимание взаимовлияние между конкретно выбранными целями. Более того, границы неулучшаемых решений могут быть и не достигнуты, так что определенные решения являются по существу недостижимыми.
Метод ![]() -ограничений
-ограничений
Некий определенный способ, который отчасти позволяет преодолеть проблему выпуклости метода взвешенных сумм, есть метод ![]() -ограничений. В этом случае осуществляется минимизация основной цели
-ограничений. В этом случае осуществляется минимизация основной цели ![]() и при представлении остальных целей в форме ограничений типа неравенств.
и при представлении остальных целей в форме ограничений типа неравенств.
|
| (3-52) |
при выполнении условия
![]()
Подобный подход позволяет определить некое количество неулучшаемых решений для случая вогнутой границы, что, по существу, является недоступным в методе взвешенных сумм, например, в точке искомого решения ![]() и
и ![]() . Однако проблемой данного метода является подходящий выбор
. Однако проблемой данного метода является подходящий выбор ![]() , который мог бы гарантировать допустимость некого решения.
, который мог бы гарантировать допустимость некого решения.
Метод достижения цели.
Описанный далее метод представляет собой метод достижения цели Гембики. Данный метод включает в себя выражение для множества намерений разработчика ![]() , которое связано с множеством целей
, которое связано с множеством целей ![]() . Такая формулировка задачи допускает, что цели могут быть или недо- или передостижимыми, и что дает разработчику возможность относительно точно выразить исходные намерения. Относительная степень недо- или передостижимости поставленных намерений контролируется посредством вектора взвешенных коэффициентов
. Такая формулировка задачи допускает, что цели могут быть или недо- или передостижимыми, и что дает разработчику возможность относительно точно выразить исходные намерения. Относительная степень недо- или передостижимости поставленных намерений контролируется посредством вектора взвешенных коэффициентов ![]() и может быть представлена как стандартная задача оптимизации с помощью следующей формулировки
и может быть представлена как стандартная задача оптимизации с помощью следующей формулировки
|
| (3-53) |
При условии, что
![]()
Член ![]() вносит в данную задачу элемент ослабления, что, иначе говоря, обозначает жесткость заданного намерения. Весовой вектор w дает исследователю возможность достаточно точно выразить меру взаимосвязи между двумя целями. Например, установка весового вектора w как равного исходному намерению указывает на то, что достигнут тот же самый процент недо- или передостижимости цели
вносит в данную задачу элемент ослабления, что, иначе говоря, обозначает жесткость заданного намерения. Весовой вектор w дает исследователю возможность достаточно точно выразить меру взаимосвязи между двумя целями. Например, установка весового вектора w как равного исходному намерению указывает на то, что достигнут тот же самый процент недо- или передостижимости цели ![]() . Посредством установки в ноль отдельного весового коэффициента (т.е.
. Посредством установки в ноль отдельного весового коэффициента (т.е. ![]() ) можно внести жесткие ограничения в поставленную задачу. Метод достижения цели обеспечивает подходящую интуитивную интерпретацию поставленной исследовательской задачи и которая, в свою очередь, является вполне разрешимой с помощью стандартных процедур оптимизации.
) можно внести жесткие ограничения в поставленную задачу. Метод достижения цели обеспечивает подходящую интуитивную интерпретацию поставленной исследовательской задачи и которая, в свою очередь, является вполне разрешимой с помощью стандартных процедур оптимизации.
Метод множителей Лагранжа позволяет отыскивать максимум или минимум функции при ограничениях-равенствах. Основная идея метода состоит в переходе от задачи на условный экстремум к задаче отыскания безусловного экстремума некоторой построенной функции Лагранжа. Пусть задана задача НП при ограничениях-равенствах вида
минимизировать ![]() (5.2.1)
(5.2.1)
при ограничениях
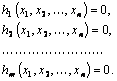 (5.2.2)
(5.2.2)
Предположим, что все функции ![]() – дифференцируемы. Введем набор переменных
– дифференцируемы. Введем набор переменных ![]() (число которых равняется числу ограничений), которые называются множителями Лагранжа, и составим функцию Лагранжа такого вида:
(число которых равняется числу ограничений), которые называются множителями Лагранжа, и составим функцию Лагранжа такого вида:
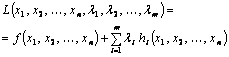 (5.2.3)
(5.2.3)
Справедливо такое утверждение [18]: для того чтобы вектор ![]() являлся решением задачи (5.2.1) при ограничениях (5.2.2), необходимо, чтобы существовал такой вектор
являлся решением задачи (5.2.1) при ограничениях (5.2.2), необходимо, чтобы существовал такой вектор ![]() , что пара векторов удовлетворяла бы системе уравнений
, что пара векторов удовлетворяла бы системе уравнений
![]() (5.2.4)
(5.2.4)
![]() (5.2.5)
(5.2.5)
множителей Лагранжа, который состоит из следующих шагов.
Составляют функцию Лагранжа ![]()
Находят частные производные ![]()
Решают систему уравнений
 (5.2.16)
(5.2.16)
и отыскивают точки ![]() , удовлетворяющие системе (5.2.16).
, удовлетворяющие системе (5.2.16).
Найденные точки ![]() дальше исследуют на максимум (или минимум).
дальше исследуют на максимум (или минимум).
Седловая точка и задача нелинейного программирования
Рассмотрим функцию Лагранжа ![]()
Определение Пара векторов ![]() называется седловой точкой функции Лагранжа
называется седловой точкой функции Лагранжа ![]() , если при всех
, если при всех ![]() выполняется условие
выполняется условие
![]() (5.3.28)
(5.3.28)
Неравенство (5.3.28) называют неравенством для седловой точки. Очевидно, что в седловой точке выполняется условие
![]() (5.3.29)
(5.3.29)
Между понятием седловой точки функции Лагранжа ![]() и решением задачи НП существует взаимосвязь, которая устанавливается в следующей теореме.
и решением задачи НП существует взаимосвязь, которая устанавливается в следующей теореме.
Теорема 5.9. Пусть ![]() и все
и все ![]() выпуклы и функции
выпуклы и функции ![]() удовлетворяют условию регулярности Слейтера. Вектор
удовлетворяют условию регулярности Слейтера. Вектор ![]() является решением задачи НП (5.3.1), (5.3.2) тогда и только тогда, когда существует такой вектор
является решением задачи НП (5.3.1), (5.3.2) тогда и только тогда, когда существует такой вектор ![]() , что
, что
![]() (5.3.30)
(5.3.30)
и
![]() (5.3.31)
(5.3.31)
Теорема Куна-Таккера. Пусть функции ![]() , имеют непрерывные частные производные на некотором открытом множестве
, имеют непрерывные частные производные на некотором открытом множестве ![]() , содержащем точку
, содержащем точку ![]() . Если
. Если ![]() является точкой минимума функции
является точкой минимума функции ![]() при ограничениях
при ограничениях ![]() , удовлетворяющих условию регулярности в виде линейной независимости векторов
, удовлетворяющих условию регулярности в виде линейной независимости векторов ![]() , то существуют такие неотрицательные множители Лагранжа
, то существуют такие неотрицательные множители Лагранжа ![]() , что
, что
![]() (5.3.15)
(5.3.15)
![]() (5.3.16)
(5.3.16)
Определим функцию Лагранжа следующим образом:
![]() (5.3.17)
(5.3.17)
Тогда теорему Куна-Таккера можно записать в виде
![]() (5.3.18)
(5.3.18)
![]() (5.3.19)
(5.3.19)
![]() (5.3.20)
(5.3.20)
Заметим, что множители Лагранжа ![]() в задаче НП с ограничениями-равенствами являются знаконеопределенными, тогда как в теореме Куна-Таккера они должны быть положительными.
в задаче НП с ограничениями-равенствами являются знаконеопределенными, тогда как в теореме Куна-Таккера они должны быть положительными.
Каждой задаче линейного программирования соответствует двойственная задача. Двойственная задача по отношению к исходной задаче строится по следующим правилам:
· Если исходная задача ставится на максимум, то двойственная ставится на минимум и наоборот.
· Коэффициенты целевой функции исходной задачи становятся правыми частями ограничений двойственной задачи. Правые части ограничений исходной задачи становятся коэффициентами целевой функции двойственной задачи.
· Если A-матрица коэффициентов исходной задачи, то транспонированная матрица T A будет матрицей коэффициентов двойственной задачи.
· В задаче на максимум все ограничения имеют знак ≤ (=), а в задаче на минимум все ограничения имеют знак ≥ .
· Число переменных в двойственной задаче равно числу ограничений в исходной задаче. Каждому ограничению исходной задачи соответствует переменная двойственной задачи. Если ограничение исходной задач имеет знак (≥ ), то соответствующая переменная двойственной задачи неотрицательна. Если ограничение имеет знак (=), то соответствующая переменная двойственной задачи может принимать положительные и отрицательные значения и наоборот.
Градиентные методы гладкой оптимизации. Общая идея градиентного спуска (подъема). Пропорциональный градиентный метод. Полношаговый градиентный метод. Метод сопряженных градиентов.Методы отыскания экстремума, использующие производные, имеют строгое математическое обоснование. Известно, что при отыскании экстремума не существует лучшего направления, чем движение по градиенту.
Градиентом дифференцируемой функции f(x) в точке х[0] называется n-мерный вектор f(x[0]), компоненты которого являются частными производными функции f(х), вычисленными в точке х[0], т. е.
f'(x[0]) = (дf(х[0])/дх1, …, дf(х[0])/дхn)T.
Этот вектор перпендикулярен к плоскости, проведенной через точку х[0] , и касательной к поверхности уровня функции f(x), проходящей через точку х[0] .В каждой точке такой поверхности функция f(x) принимает одинаковое значение. Приравнивая функцию различным постоянным величинам С0, С1, ... , получим серию поверхностей, характеризующих ее топологию
Вектор-градиент направлен в сторону наискорейшего возрастания функции в данной точке. Вектор, противоположный градиенту (-f’(х[0])), называется антиградиентом и направлен в сторону наискорейшего убывания функции. В точке минимума градиент функции равен нулю. На свойствах градиента основаны методы первого порядка, называемые также градиентным и методами минимизации. Использование этих методов в общем случае позволяет определить точку локального минимума функции.
Очевидно, что если нет дополнительной информации, то из начальной точки х[0] разумно перейти в точку х [1], лежащую в направлении антиградиента - наискорейшего убывания функции. Выбирая в качестве направления спуска р[k] антиградиент -f’(х[k]) в точке х[k], получаем итерационный процесс вида
х[k+1] = x[k]-akf'(x[k]), аk> 0; k=0, 1, 2, ...
В координатной форме этот процесс записывается следующим образом:
xi[k+1]=хi[k] - ak![]() f(x[k])/
f(x[k])/![]() xi
xi
i = 1, ..., n; k= 0, 1, 2,...
В качестве критерия останова итерационного процесса используют либо выполнение условия малости приращения аргумента || x[k+l] - x[k] || <= e, либо выполнение условия малости градиента
|| f’(x[k+l]) || <= g,
Здесь e и g - заданные малые величины.
Возможен и комбинированный критерий, состоящий в одновременном выполнении указанных условий. Градиентные методы отличаются друг от друга способами выбора величины шага аk.
При методе с постоянным шагом для всех итераций выбирается некоторая постоянная величина шага. Достаточно малый шаг аk обеспечит убывание функции, т. е. выполнение неравенства
f(х[k+1]) = f(x[k] – akf’(x[k])) < f(x[k]).
Однако это может привести к необходимости проводить неприемлемо большое количество итераций для достижения точки минимума. С другой стороны, слишком большой шаг может вызвать неожиданный рост функции либо привести к колебаниям около точки минимума (зацикливанию). Из-за сложности получения необходимой информации для выбора величины шага методы с постоянным шагом применяются на практике редко.
Более экономичны в смысле количества итераций и надежности градиентные методы с переменным шагом, когда в зависимости от результатов вычислений величина шага некоторым образом меняется. Рассмотрим применяемые на практике варианты таких методов.
Метод наискорейшего спуска
При использовании метода наискорейшего спуска на каждой итерации величина шага аk выбирается из условия минимума функции f(x) в направлении спуска, т. е.
f(x[k] –akf’(x[k])) = ![]() f(x[k] – af'(x[k])).
f(x[k] – af'(x[k])).
Это условие означает, что движение вдоль антиградиента происходит до тех пор, пока значение функции f(x) убывает. С математической точки зрения на каждой итерации необходимо решать задачу одномерной минимизации по а функции
j(a) = f(x[k] - af'(x[k])) .
Алгоритм метода наискорейшего спуска состоит в следующем.
1. Задаются координаты начальной точки х[0].
2. В точке х[k], k = 0, 1, 2, ... вычисляется значение градиента f’(x[k]).
3. Определяется величина шага ak, путем одномерной минимизации по а функции j(a) = f(x[k] - af'(x[k])).
4. Определяются координаты точки х[k+1]:
хi[k+1] = xi[k] – аkf’i(х[k]), i = 1 ,..., п.
5. Проверяются условия останова стерационного процесса. Если они выполняются, то вычисления прекращаются. В противном случае осуществляется переход к п. 1.
В рассматриваемом методе направление движения из точки х[k] касается линии уровня в точке x[k+1] (Рис. 2.9). Траектория спуска зигзагообразная, причем соседние звенья зигзага ортогональны друг другу. Действительно, шаг ak выбирается путем минимизации по а функции φ(a) = f(x[k] - af'(x[k])). Необходимое условие минимума функции dj(a)/da = 0. Вычислив производную сложной функции, получим условие ортогональности векторов направлений спуска в соседних точках:
dj(a)/da = -f’(x[k+1]f’(x[k]) = 0.
Градиентные методы сходятся к минимуму с высокой скоростью (со скоростью геометрической прогрессии) для гладких выпуклых функций. У таких функций наибольшее М и наименьшее m собственные значения матрицы вторых производных (матрицы Гессе)
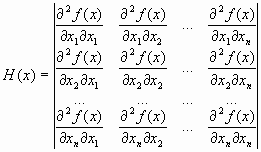
мало отличаются друг от друга, т. е. матрица Н(х) хорошо обусловлена. Напомним, что собственными значениями li, i =1, …, n, матрицы являются корни характеристического уравнения
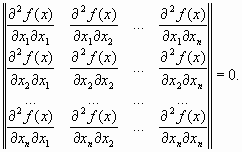
Однако на практике, как правило, минимизируемые функции имеют плохо обусловленные матрицы вторых производных (т/М << 1). Значения таких функций вдоль некоторых направлений изменяются гораздо быстрее (иногда на несколько порядков), чем в других направлениях. Их поверхности уровня в простейшем случае сильно вытягиваются, а в более сложных случаях изгибаются и представляют собой овраги. Функции, обладающие такими свойствами, называют овражными. Направление антиградиента этих функций (см. Рис. 2.10) существенно отклоняется от направления в точку минимума, что приводит к замедлению скорости сходимости.
Метод сопряженных градиентов
Рассмотренные выше градиентные методы отыскивают точку минимума функции в общем случае лишь за бесконечное число итераций. Метод сопряженных градиентов формирует направления поиска, в большей мере соответствующие геометрии минимизируемой функции. Это существенно увеличивает скорость их сходимости и позволяет, например, минимизировать квадратичную функцию
f(x) = (х, Нх) + (b, х) + а
с симметрической положительно определенной матрицей Н за конечное число шагов п , равное числу переменных функции. Любая гладкая функция в окрестности точки минимума хорошо аппроксимируется квадратичной, поэтому методы сопряженных градиентов успешно применяют для минимизации и неквадратичных функций. В таком случае они перестают быть конечными и становятся итеративными.
По определению, два n-мерных вектора х и у называют сопряженными по отношению к матрице H (или H-сопряженными), если скалярное произведение (x, Ну) = 0. Здесь Н - симметрическая положительно определенная матрица размером пхп.
Одной из наиболее существенных проблем в методах сопряженных градиентов является проблема эффективного построения направлений. Метод Флетчера-Ривса решает эту проблему путем преобразования на каждом шаге антиградиента -f(x[k]) в направление p[k], H-сопряженное с ранее найденными направлениями р[0], р[1], ..., р[k-1]. Рассмотрим сначала этот метод применительно к задаче минимизации квадратичной функции.
Направления р[k] вычисляют по формулам:
p[k] = -f’(x[k])+bk-1p[k-l], k >= 1;
p[0] = -f’(x[0]).
Величины bk-1 выбираются так, чтобы направления p[k], р[k-1] были H-сопряженными:
(p[k], Hp[k-1])= 0.
В результате для квадратичной функции
![]() ,
,
итерационный процесс минимизации имеет вид
x[k+l] =x[k] +akp[k],
где р[k] - направление спуска на k-м шаге; аk - величина шага. Последняя выбирается из условия минимума функции f(х) по а в направлении движения, т. е. в результате решения задачи одномерной минимизации:
f(х[k] + аkр[k]) = ![]() f(x[k] + ар [k]).
f(x[k] + ар [k]).
Для квадратичной функции
![]()
Алгоритм метода сопряженных градиентов Флетчера-Ривса состоит в следующем.
1. В точке х[0] вычисляется p[0] = -f’(x[0]).
2. На k-м шаге по приведенным выше формулам определяются шаг аk. и точка х[k+1].
3. Вычисляются величины f(x[k+1]) и f’(x[k+1]).
4. Если f’(x[k+1]) = 0, то точка х[k+1] является точкой минимума функции f(х). В противном случае определяется новое направление p[k+l] из соотношения
![]()
и осуществляется переход к следующей итерации. Эта процедура найдет минимум квадратичной функции не более чем за п шагов. При минимизации неквадратичных функций метод Флетчера-Ривса из конечного становится итеративным. В таком случае после (п+1)-й итерации процедуры 1-4 циклически повторяются с заменой х[0] на х[п+1] , а вычисления заканчиваются при ![]() , где
, где ![]() - заданное число. При этом применяют следующую модификацию метода:
- заданное число. При этом применяют следующую модификацию метода:
x[k+l] = x[k] +akp[k],
p[k] = -f’(x[k])+bk-1p[k-l], k >= 1;
p[0] = -f’(x[0]);
f(х[k] + akp[k]) = ![]() f(x[k] + ap[k];
f(x[k] + ap[k];
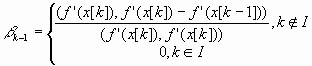 .
.
Здесь I- множество индексов: I = {0, n, 2п, Зп, ...}, т. е. обновление метода происходит через каждые п шагов.
Геометрический смысл метода сопряженных градиентов состоит в следующем (Рис. 2.11). Из заданной начальной точки х[0] осуществляется спуск в направлении р[0] = -f'(x[0]). В точке х[1] определяется вектор-градиент f'(x [1]). Поскольку х[1] является точкой минимума функции в направлении р[0], то f’(х[1]) ортогонален вектору р[0]. Затем отыскивается вектор р [1], H-сопряженный к р [0] . Далее отыскивается минимум функции вдоль направления р[1] и т. д.
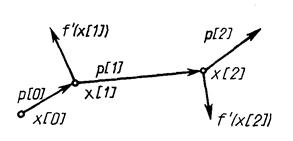
Рис. 2.11. Траектория спуска в методе сопряженных градиентов
Методы сопряженных направлений являются одними из наиболее эффективных для решения задач минимизации. Однако следует отметить, что они чувствительны к ошибкам, возникающим в процессе счета. При большом числе переменных погрешность может настолько возрасти, что процесс придется повторять даже для квадратичной функции, т. е. процесс для нее не всегда укладывается в п шагов.
Выпуклая оптимизация. Условие выпуклости. Субградиентный метод выпуклой оптимизации. Метод растяжения пространства. Метод эллипсоидов.Основная задача выпуклого программирования
Пусть задано выпуклое и замкнутое множество ![]() . Рассмотрим множество
. Рассмотрим множество
![]() ={
={![]() },
}, ![]() =(
=(![]() ,…,
,…,![]() ),
), ![]() Î
Î![]() .
.
где ![]() (
(![]() ) — вогнутые (выпуклые вверх) непрерывные на
) — вогнутые (выпуклые вверх) непрерывные на ![]() скалярные функции. В теории математического программирования каждый элемент
скалярные функции. В теории математического программирования каждый элемент ![]() Î
Î![]() принято называть допустимым планом, а само множество
принято называть допустимым планом, а само множество ![]() — множеством допустимых планов.
— множеством допустимых планов.
Формальная постановка задачи выпуклого программирования
Задачу
![]() ,
,
где ![]() выпукла, а
выпукла, а ![]() определяется вышеприведенными условиями, называется основной задачей выпуклого программирования.
определяется вышеприведенными условиями, называется основной задачей выпуклого программирования.
Определение означает, что ставится задача:
Если существует минимальное значение функции ![]() на множестве
на множестве ![]() , то среди всех допустимых планов найти оптимальный план
, то среди всех допустимых планов найти оптимальный план ![]() , для которого
, для которого
![]() =
=![]() =
=![]()
при этом число ![]() называют значением задачи.
называют значением задачи.
Если оптимального плана не существует, то требуется
· либо найти значение задачи как точную нижнюю грань значений функции ![]() на множестве
на множестве ![]() :
:
![]() =
=![]()
· либо убедиться, что ![]() неограничена снизу на множестве
неограничена снизу на множестве ![]() ;
;
· либо убедиться в том, что множество допустимых планов ![]() пусто.
пусто.
Для решения предложенной оптимизационной задачи следует выполнить следующие действия:
· Определить множество ![]() .
.
· Определить вектор-функцию ![]() =(
=(![]() ,…,
,…,![]() ) и вектор
) и вектор ![]() Î
Î![]() .
.
· Определить множество допустимых планов ![]() ={
={![]() }.
}.
· Привести задачу к стандартной форме основной задачи выпуклого программирования и определить оптимизируемую функцию ![]() .
.
· Проверить, является ли полученная оптимизационная задача ЗВП, для этого
· проверить на выпуклость множество ![]() ;
;
· проверить на выпуклость функцию ![]() .
.
В случае успеха п. 5
· Построить функцию Лагранжа полученной ЗВП.
· С помощью дифференциальных условий Куна-Таккера найти седловые точки построенной функции Лагранжа.
В случае неудачи п. 5 попытаться найти другие методы решения задачи.
Методы субградиентной оптимизации. Эти итеративные процедуры формируют последовательность векторов {lk}. Начиная с некоторого начального значения l0 эти вектора меняются по следующему правилу
lk+1 = lk +tk (A xk - b),
где xk — оптимальное решение задачи ![]() , а tk — размер шага. Фундаментальный теоретический результат заключается в том, что [14]
, а tk — размер шага. Фундаментальный теоретический результат заключается в том, что [14]
![]() .
.
Размер шага на практике обычно выбирают, следуя [11],
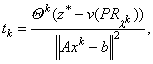
где q k — скаляр, 0 < q k![]() 2 и z* — верхняя граница для n(D). Обычно z* получают эвристикой для P. В методе ветвей и границ z* — текущий рекорд. Последовательность q k, как правило, начинается с q 0=2 и затем q k делится пополам, через фиксированное число итераций, зависящее от размерности задачи.
2 и z* — верхняя граница для n(D). Обычно z* получают эвристикой для P. В методе ветвей и границ z* — текущий рекорд. Последовательность q k, как правило, начинается с q 0=2 и затем q k делится пополам, через фиксированное число итераций, зависящее от размерности задачи.
Функциональный анализ, часть современной математики, главной задачей которой является изучение бесконечномерных пространств и их отображений. Наиболее изучены линейные пространства и линейные отображения. Для Ф. а. характерно сочетание методов классического анализа, топологии и алгебры. Абстрагируясь от конкретных ситуаций, удаётся выделить аксиомы и на их основе построить теории, включающие в себя классические задачи как частный случай и дающие возможность решать новые задачи. Сам процесс абстрагирования имеет самостоятельное значение, проясняя ситуацию, отбрасывая лишнее и открывая неожиданные связи. В результате удаётся глубже проникнуть в сущность математических понятий и проложить новые пути исследования.
Развитие Ф. а. происходило параллельно с развитием современной теоретической физики, при этом выяснилось, что язык Ф. а. наиболее адекватно отражает закономерности квантовой механики, квантовой теории поля и т.п. В свою очередь эти физические теории оказали существенное влияние на проблематику и методы Ф. а.
Похожие работы
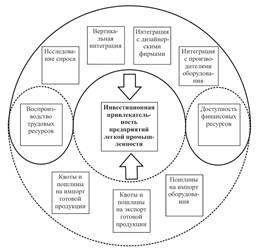
... результаты диссертации используются в учебном процессе филиала Московского энергетического института (технического университета) в г. Смоленске. Предложные механизмы и метод повышения инвестиционной привлекательности предприятий легкой промышленности в условиях глобализации могут быть практически использовании федеральными и региональными органами власти при разработке инвестиционных программ ...
... кооперации как оптимальном пути модернизации крестьянских хозяйств находят свое применение в современных странах «третьего мира». А.В. Чаянов, пожалуй, по направленности своих теорий один из самых “русских” экономистов. И это неудивительно: ведь он занимался вопросами крестьянских хозяйств. Он тщательно проанализировал структуру обычного крестьянского хозяйства и пришел к выводу о его необычайной ...
... важности факторы, определяющие моральное состояние их подчиненных, они, как правило, осведомленность о состоянии дел в организации относят на последнее место. Сознание человека не терпит вопросов без ответов. Если те, кто знает, не дают ответов на вопросы, тогда работники будут искать ответы там, где нет достоверной информации Неправильная установка сознания и качество коммуникаций. Установка ...
... для нее рисков, и предопределило цель и задачи данной работы. Целью диссертационной работы является разработка двухкритериальных целочисленных моделей и методов управления портфельными инвестициями, учитывающих требования по повышению доходности и снижению рыночных рисков финансовых инвестиций и ограничения реального сектора экономики при инвестициях в производственные запасы. Для достижения ...
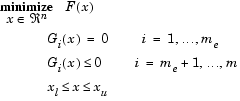
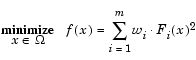





0 комментариев