Навигация
Критерий среднего выигрыша
1. Критерий среднего выигрыша
Предполагает задание вероятностей состояния обстановки Рi. Эффективность систем оценивается как среднее ожидание (мат. ожидание) оценок эффективности по всем состояниям обстановки. Оптимальной системе будет соответствовать максимальная оценка.
К = ∑ РiКij
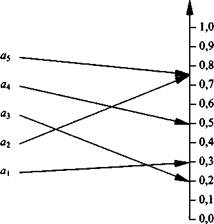
Предположим, что вероятность применения противником программных воздействий Р1 = 0,4; Р2=0,1; Р3=0,1; Р4=0,3
К(а1)=0,4*0,1+0,5*0,2+0,1*0,1+0,3*0,2=0,21
К(а2)=0,4*0,2+0,2*0,3+0,1*0,2+0,3*0,4=0,28
К(а3)=0,4*0,1+0,2*0,4+0,1*0,4+0,3*0,3=0,25
Оптимальное решение по данному критерию - программный продукт а2.
2. Критерий Лапласа (достаточного основания)
Предполагается, что состояние обстановки равновероятно, так как нет достаточных оснований предполагать иное.
К=1/к∑Кij, для каждого i,
а оптимальное значение указывает максимальную сумму К.
Р1=0,25; Р2=0,25; Р3=0,25; Р4=0,25
К(а1)=0,25*(0,1+0,5+0,1+0,2)=0,225
К(а2)=0,25*(0,2+0,3+0,2+0,4)=0,275
К(а3)=0,25*(0,1+0,4+0,4+0,3)=0,3
Оптимальное решение - программа а3Замечание – критерий Лапласа – это частный случай критерия среднего выигрыша.
3. Критерий осторожного наблюдателя (критерий Вальда)
Это максимальный критерий (максимальные доходы, минимальные потери). Он гарантирует определенный выигрыш при худших условиях. Критерий использует то, что при неизвестной обстановке нужно поступать самым осторожным образом, ориентируясь на минимальное значение эффекта каждой системы.
Для этого в каждой строке матрицы находится минимальная из оценок систем
К(аi) min Кij.
j
Оптимальной считается система из строки с максимальным значением эффективности
Копт=max (minKij) для всех ij
i j
К(а1)=min(0,1;0,5;0,1;0,2)=0,1
К(а2)=min(0,2;0,3;0,2;0,4)=0,2
К(а3)=min(0,1;0,4;0,4;0,3)=0,1
Оптимальное решение – продукт а2
В любом состоянии обстановки выбранная система покажет результат не хуже найденного максимина. Однако такая осторожность является в ряде случаев недостатком критерия.
4. Критерий пессимизма-оптимизма (критерий Гурвица)
Критерий обобщенного максимина. Согласно данному критерию при оценке и выборе систем не разумно проявлять как осторожность, так и азарт. Следует принимать во внимание самое высокое и самое низкое значение эффективности и занимать промежуточную позицию. Эффективность находится как взвешенная с помощью коэффициента α сумма максимальных и минимальных оценок.
К(ai) = α max Kij+(1- α)*min Kij
j j
0≤ α ≤1
Копт = max { α max Kij+(1+ α)*min Kij}
i j j
d=0,6
К(а1)=0,6*0,5+(1-0,6)*0,1=0,34
К(а2)=0,6*0,4+(1-0,6)*0,2=0,32
К(а3)=0,6*0,4+(1-0,6)*0,1=0,28
Оптимальное решение – продукт а1
При α = 0 критерий Гурвица сводится к критерию максимина. На практике используются значения α из интервала (0,3÷0,7).
5. Критерий минимального риска (критерий Севиджа)
Минимизирует потери эффективности при наихудших условиях. В этом случае матрица эффективности должна быть преобразована в матрицу потерь. Каждый элемент определяется как разность между максимальным и текущим значениями оценок эффективности в столбце.
∆ Кij= maxKij- Kij
После преобразования матрицы используется критерий минимакса, т.е. оптимального решения критерия.
K(ai)=max∆ Кij
j
Kопт=min (max∆ Кij)
i j
Матрица потерь
| а\к | к1 | к2 | к3 | к4 | к(аi) |
| а1 | 0,1 | 0 | 0,3 | 0,2 | 0,3 |
| а2 | 0 | 0,2 | 0,2 | 0 | 0,2 |
| а3 | 0,1 | 0,1 | 0 | 0,1 | 0,1 |
Оптимальное решение – продукт а3
Комментарий: критерий отражает сожаления по поводу того, что выбранная система не оказалась лучшей при определении состава обстановки. Например, если выбрать программу а1, а угрозу n3, то сожаление, что не выбрана лучшая из программ а3 составит 0,3.
Таким образом, эффективность систем в неопределенных операциях может оцениваться по ряду критериев. На выбор каждого из них может влиять ряд факторов:
а) природа конкретных операций и ее цель
- в одном случае допустим риск
- в другом - гарантированный результат
б) причина неопределенности
- закон природы
- разумные действия противника
в) характер лица, принимающего решение:
- склонность добиться большего, идя на риск
- всегда осторожные действия
Результаты всех расчётов записываются в одну таблицу.
Таблица. Форма записи результатов| а\к | к1 | к2 | к3 | к4 | Ср. выигр | Лапласа | Вальда | Гурвица | Севиджа |
| а1 | 0,1 | 0,5 | 0,1 | 0,2 | 0,21 | 0,225 | 0,1 | 0,34 | 0,3 |
| а2 | 0,2 | 0,3 | 0,2 | 0,4 | 0,28 | 0,275 | 0,2 | 0,32 | 0,2 |
| а3 | 0,1 | 0,4 | 0,4 | 0,3 | 0,25 | 0,300 | 0,1 | 0,28 | 0,1 |
Тип критерия для выбора рационального варианта выбирается на аналитической стадии рассмотрения сложных систем.
Задание
По каждому из приведенных выше критериев найти решение задачи.
Представить в виде таблицы «Форма записи результатов»
Вариант 1
В ресторане решено делать бизнес-ланч.
Процесс производства позволяет изготавливать 70, 120 или 150 бизнес-ланчей. Число посетителей колеблется от 60 до 160. Необходимо определить число изготавливаемых бизнес-ланчей аi, если число посетителей kj.
Матрица эффективности имеет вид (руб.).
| а/ к | к1 = 60 | к2= 95 | к3= 125 | к4= 160 |
| а1= 70 | -1600 | 2300 | 2300 | 2300 |
| а2= 120 | -4000 | 5300 | 7800 | 7800 |
| а3= 150 | -6200 | -1750 | 10000 | 9500 |
Вариант 2
Транспортное предприятие организует пригородные автобусные рейсы. Ежедневное число пассажиров изменяется в интервале от 200 до 300 человек. Необходимо определить число рейсов аi, если число пассажиров kj. Матрица эффективности имеет вид (руб.).
| а/к | к1 = 200 | к2= 225 | к3= 250 | к4= 300 |
| а1= 8 | 12300 | 12300 | 12300 | 12300 |
| а2= 10 | 10000 | 16400 | 16520 | 17900 |
| а3= 12 | 8000 | 15000 | 17250 | 19500 |
| а4= 14 | 6000 | 10500 | 17240 | 18560 |
Вариант 3
Туристическая фирма планирует организовать маршрут по Карелии. Число туристов за сезон ожидается от 10 до 16 тысяч человек. Группы формируются по 20 чел. Необходимо определить число маршрутов аi, если число туристов kj. Матрица эффективности имеет вид (тыс.руб.)
| а/к | к1 = 10000 | к2= 12000 | к3= 14000 | к4= 16000 |
| а1= 500 | 125 | 214 | 189 | 120 |
| а2= 600 | 246 | 440 | 260 | 260 |
| а3= 700 | 126 | 135 | 590 | 600 |
| а4= 800 | 100 | 123 | 580 | 853 |
Вариант 4
У предпринимателя есть идея организовать сервисный центр. По прогнозным оценкам ожидается от 90 до 150 клиентов в месяц. На одном рабочем месте можно обслужить 20 человек в месяц. Определить число рабочих мест аi, если число клиентов kj. Матрица эффективности имеет вид (тыс. руб.)
| а/к | к1 = 90 | к2= 110 | к3= 130 | к4= 150 |
| а1= 5 | 30 | 31 | 32 | 32 |
| а2= 6 | 42 | 44 | 26 | 26 |
| а3= 7 | 36 | 136 | 190 | 170 |
| а4= 8 | 25 | 23 | 150 | 175 |
Вариант 5
Решено организовать тренажерный зал. По прогнозным оценкам ожидается от 80 до 150 посетителей в день. Определить, сколько закурить тренажёров аi, если число посетителей kj. Матрица эффективности имеет вид (тыс. руб.)
| а/к | к1 = 80 | к2= 110 | к3= 130 | к4= 150 |
| а1= 8 | 3050 | 3180 | 3240 | 3210 |
| а2= 11 | 4270 | 4410 | 2650 | 2690 |
| а3= 13 | 3690 | 13620 | 19070 | 17030 |
| а4= 15 | 2570 | 2330 | 15060 | 17560 |
Вариант 6
В ресторане решено делать бизнес-ланч.
Процесс производства позволяет изготавливать 80,120 или160 бизнес-ланчей. Число посетителей колеблется от 70 до 160. Необходимо определить число изготавливаемых бизнес-ланчей аi, если число посетителей kj.
Матрица эффективности имеет вид (руб).
| а/ к | к1 = 80 | к2= 110 | к3= 140 | к4= 160 |
| а1= 80 | -1200 | 3300 | 3300 | 3300 |
| а2= 120 | -4500 | 5400 | 7890 | 7890 |
| а3= 160 | -6800 | -2750 | 11000 | 10500 |
Вариант 7
Транспортное предприятие организует пригородные автобусные рейсы. Ежедневное число пассажиров изменяется в интервале от 400 до 550 человек. Необходимо определить число рейсов аi, если число пассажиров kj. Матрица эффективности имеет вид (руб.).
| а/к | к1 = 400 | к2= 450 | к3= 500 | к4= 550 |
| а1= 12 | 24600 | 24600 | 24600 | 24600 |
| а2= 14 | 20000 | 19400 | 19520 | 18900 |
| а3= 16 | 15500 | 15000 | 21250 | 19500 |
| а4= 18 | 8500 | 10500 | 27240 | 29560 |
Вариант 8
Туристическая фирма планирует организовать маршрут по Карелии. Число туристов за сезон ожидается от 5 до 8 тысяч человек. Группы формируются по 20 чел. Необходимо определить число маршрутов аi, если число туристов kj. Матрица эффективности имеет вид (тыс. руб.)
| а/к | к1 = 5000 | к2= 6000 | к3= 7000 | к4= 8000 |
| а1= 250 | 63 | 108 | 99 | 60 |
| а2= 300 | 123 | 256 | 136 | 130 |
| а3= 350 | 66 | 77 | 280 | 320 |
| а4= 400 | 59 | 66 | 290 | 472 |
Вариант 9
У предпринимателя есть идея организовать сервисный центр. По прогнозным оценкам ожидается от 90 до 150 клиентов в месяц. На одном рабочем месте можно обслужить 20 человек в месяц. Определить число рабочих мест аi, если число клиентов kj. Матрица эффективности имеет вид (тыс. руб.)
| а/к | к1 = 90 | к2= 110 | к3= 130 | к4= 150 |
| а1= 5 | 60 | 70 | 70 | 68 |
| а2= 6 | 46 | 48 | 36 | 38 |
| а3= 7 | 55 | 139 | 211 | 179 |
| а4= 8 | 29 | 44 | 231 | 198 |
Вариант 10
Решено организовать тренажерный зал. По прогнозным оценкам ожидается от 80 до 150 посетителей в день. Определить, сколько закурить тренажёров аi, если число посетителей kj. Матрица эффективности имеет вид (тыс. руб.)
| а/к | к1 = 80 | к2= 110 | к3= 130 | к4= 150 |
| а1= 8 | 7890 | 7856 | 8899 | 5678 |
| а2= 11 | 6543 | 6677 | 4455 | 4422 |
| а3= 13 | 4432 | 23456 | 24567 | 31900 |
| а4= 15 | 6432 | 3524 | 24312 | 30954 |
Задание 6. Постановка задачи математического программирования
В процессе принятия решений часто необходимо вербальное описание проблемы преобразовать в формальное описание задачи и затем использовать известный метод её решения.
Для того, чтобы возникла задача, необходимо определить допустимую область решений, определить факторы, влияющие на это решение. Для формализации задачи нужно определить количественные зависимости между факторами и результатами; в совокупности они образуют ограничения на деятельность системы. При постановке экстремальной задачи, среди ограничений выделяют одно или несколько и используют их в качестве критерия (простого или сложного, сконструированного из нескольких).
В результате постановка задачи математического программирования сводится к формированию ограничений деятельности системы, которые затем разделяются на критерии и ограничения. Критерий позволяет оценить решения и определить лучшее из них.
Постановка задачи сводится к переводу словесного описания ситуации в формализованное, в котором определяется переменная, ограничения и целевая функция.
Постановка любой задачи заключается в том, чтобы перевести их словесное описание в формальное. Широкое распространение получили модели математического программирования.
Задача математического программирования состоит в нахождении оптимального (максимального или минимального) значения целевой функции, переменные которой принадлежат некоторой области допустимых значений. Наиболее наглядными являются задача линейного программирования (ЗЛП) и транспортная задача.
ЗЛП состоит в определении минимального или максимального значения целевой функции; целевая функция и ограничения и представляют собой линейные неравенства.
(F(х) = ![]() ) ®Max
) ®Max
![]() i = 1….k
i = 1….k
xj³ 0,
aij, bi, ci - заданные постоянные величины
Чтобы решить эту задачу, нужно найти такой вектор Х = (x1, x2,… xк)
(набор переменных величин xj), чтобы он доставлял максимальное значение целевой функции F (х)
На предприятии изготавливается два вида изделий из трёх видов материалов
aij – расход материала вида i на одно изделие j.
bi- запас материала вида i
ci-прибыль от одного изделия вида i.
Сформулировать ЗЛП, чтобы определить, сколько изделий каждого вида следует производить, чтобы максимизировать прибыль. Расход материалов представлен в Таблице. Таблица. Расход материала вида i на одно изделие j| Изделие (j) | Вид материала (i) | Прибыль на одно изделие | ||
| 1 | 2 | 3 | ||
| 1 | 5 | 2 | 6 | 22 |
| 2 | 7 | 8 | 4 | 14 |
| Запас материалов | 456 | 594 | 872 | |
В соответствии с вопросом, сформулированным в задаче, в качестве переменной величины выступит объём производства изделий каждого вида. Тогда:
Х1 - объём производства изделий 1-го вида
Х2 - объём производства изделий 2-го вида
Постановка задачи ЛП:
22Х1 + 14Х2 ® мах (максимизировать совокупную прибыль от
производства изделий обоих видов)
5 Х1 + 7 Х2 £ 456 – ограничение на потребление материалов 1-го вида
2 Х1 + 8 Х2 £ 594 ограничение на потребление материалов 2-го вида
6 Х1 + 4 Х2 £ 872 ограничение на потребление материалов 3-го вида
Х1, Х2 ³ 0 - изделия должны производиться
Вариант 1.
В трёх цехах изготавливаются два вида изделий.
aij – загрузка j-го цеха при изготовлении изделий, %
ci -прибыль от одного изделия вида i, руб.
Сформулировать ЗЛП, чтобы определить, сколько изделий каждого вида следует производить при возможно полной загрузке цехов, чтобы получить максимальную прибыль. Загрузка цехов представлена в Таблице.
Таблица. Загрузка цехов| Изделие (j) | № цеха (i) | Цена изделия | ||
| 1 | 2 | 3 | ||
| 1 | 5 | 3 | 4 | 488 |
| 2 | 4 | 1,2 | 5,1 | 233 |
| Максимальная загрузка | 100% | 100% | 100% | |
Имеются три склада запчастей А1, А2, А3 и три сервисных центра
Ц1, Ц2, Ц3. На складах следующее число контейнеров: А1= 14 А2=10 А3 =16; в
Транспортные затраты aij на перевозку одного компьютера со i –го склада в магазин j представлены в таблице:
| Ц1 | Ц 2 | Ц3 | |
| А1 | 3 | 4(a12) | 2 |
| А2 | 2 | 6 | 9 |
| А3 | 4 | 3 | 1 |
Составить задачу линейного программирования (целевую функцию и ограничения)
Пояснение. В качестве переменной величины использовать Хij – число перевезённых компьютеров со i –го склада в магазин j
Вариант 3
Сформулировать ЗЛП, чтобы определить, сколько изделий каждого вида следует производить, чтобы максимизировать прибыль. Расход материалов представлен в Таблице. Таблица. Расход материала вида i на одно изделие j| Изделие (j) | Вид материала (i) | Прибыль на одно изделие | ||
| 1 | 2 | 3 | ||
| 1 | 12 | 10 | 15 | 156 |
| 2 | 15 | 11 | 16 | 105 |
| 3 | 19 | 19 | 14 | 120 |
| Запас материалов | 11658 | 12999 | 13998 | |
Из двух складов А1 и А2 следует развести компьютеры по трём
магазинам В1,В 2, В3. На складах имеется: А1 =50, А2=70 компьютеров.
В магазинах требуется: В1=16,В 2=56, В3=48 компьютеров
Транспортные затраты aij на перевозку одного компьютера со i –го склада в магазин j представлены в таблице:
| В1 | В 2 | В3 | |
| А1 | 3 | 4(a12) | 2 |
| А2 | 4 | 3 | 1 |
Составить задачу линейного программирования (целевую функцию и ограничения)
Пояснение. В качестве переменной величины использовать Хij – число перевезённых компьютеров со i –го склада в магазин j
Вариант 5
На предприятии изготавливается два вида изделий из трёх видов материалов
aij – расход материала вида i на одно изделие j.
bi- запас материала вида i
ci-прибыль от одного изделия вида i.
Сформулировать ЗЛП, чтобы определить, сколько изделий каждого вида следует производить, чтобы максимизировать прибыль. Расход материалов представлен в Таблице. Таблица. Расход материала вида i на одно изделие j| Изделие (j) | Вид материала (i) | Прибыль на одно изделие | ||
| 1 | 2 | 3 | ||
| 1 | 7 | 5 | 6 | 222 |
| 2 | 66 | 12 | 24 | 144 |
| Запас материалов | 1615 | 1555 | 2139 | |
В трёх цехах изготавливаются два вида изделий.
aij – загрузка j-го цеха при изготовлении изделий, %
ci -прибыль от одного изделия вида i, руб.
Сформулировать ЗЛП, чтобы определить, сколько изделий каждого вида следует производить при возможно полной загрузке цехов, чтобы получить максимальную прибыль. Загрузка цехов представлена в Таблице.
Таблица. Загрузка цехов| Изделие (j) | № цеха (i) | Цена изделия | ||
| 1 | 2 | 3 | ||
| 1 | 15 | 13 | 7 | 256 |
| 2 | 14 | 12 | 8 | 144 |
| Максимальная загрузка | 100% | 100% | 100% | |
Из двух складов А1 и А2 следует развести компьютеры по трём магазинам. В1,В 2, В3. На складах имеется: А1 =55, А2=75 компьютеров.
В магазинах требуется: В1=26,В 2=56, В3=48 компьютеров
Транспортные затраты aij на перевозку одного компьютера со i –го склада в магазин j представлены в таблице:
| В1 | В 2 | В3 | |
| А1 | 3 | 2 | 4 |
| А2 | 2 | 3 | 1 |
Составить задачу линейного программирования (целевую функцию и ограничения)
Пояснение. В качестве переменной величины использовать Хij – число перевезённых компьютеров со i –го склада в магазин j
Вариант 8
В трёх цехах изготавливаются два вида изделий.aij – загрузка j-го цеха при изготовлении изделий, %
ci -прибыль от одного изделия вида i, руб.
Сформулировать ЗЛП, чтобы определить, сколько изделий каждого вида следует производить при возможно полной загрузке цехов, чтобы получить максимальную прибыль. Загрузка цехов представлена в Таблице.
Таблица. Загрузка цехов| Изделие (j) | № цеха (i) | Цена изделия | ||
| 1 | 2 | 3 | ||
| 1 | 43 | 143 | 75 | 25 |
| 2 | 24 | 124 | 86 | 44 |
| Максимальная загрузка | 100% | 100% | 100% | |
Вариант 9
На предприятии изготавливается два вида изделий из трёх видов материалов
aij – расход материала вида i на одно изделие j.
bi- запас материала вида i
ci-прибыль от одного изделия вида i.
Сформулировать ЗЛП, чтобы определить, сколько изделий каждого вида следует производить, чтобы максимизировать прибыль. Расход материалов представлен в Таблице. Таблица. Расход материала вида i на одно изделие j| Изделие (j) | Вид материала (i) | Прибыль на одно изделие | |
| 1 | 2 |
| |
| 1 | 17 | 22 | 2 |
| 2 | 7 | 14 | 8 |
| 3 | 5 | 5 | 10 |
| Запас материалов | 1122 | 3344 | |
Вариант 10
Из двух складов А1 и А2 следует развести коробки с цветами по трём магазинам. В1,В 2, В3. На складах имеется коробок с цветами: А1 =55, А2=75
В магазинах требуется: В1=26,В 2=56, В3=48 коробок с цветами
Транспортные затраты aij на перевозку одной коробки с цветами со i –го склада в магазин j представлены в таблице:
Таблица| В1 | В 2 | В3 | |
| А1 | 3 | 2 | 4 |
| А2 | 2 | 3 | 1 |
Составить задачу линейного программирования (целевую функцию и ограничения)
Пояснение. В качестве переменной величины использовать Хij – число перевезённых компьютеров со i –го склада в магазин j
Литература
Основная:
1.Ахундов В.М. Системный анализ в экономических исследованиях. - М., 1987.
2.Волкова В.Н, Денисов А.А. Основы теории систем и системного анализа. - СПб: СПбГТУ, 1997.
3.Моисеев Н.Н. Математические методы системного анализа. - М.: Наука, 1984.
4.![]() Перегудов Ф.И., Тарасенко Ф.П. Введение в системный анализ. - М.: Высшая школа, 1989.
Перегудов Ф.И., Тарасенко Ф.П. Введение в системный анализ. - М.: Высшая школа, 1989.
5.Системный анализ в экономике и организации производства: Учебник. - Л.: Политехника, 1994.
6.Д. Уотермен. Руководство по экспертным системам. - М.: Мир, 1989.
7.Черняк Ю.И Системный анализ в управлении экономикой. - М.: Экономика, 1975.
8.Экономико-математические методы и прикладные модели: Учебн. пос. для ВУЗов / Под ред. В.В. Федосеева. - М.: ЮНИТИ, 1999.
9.КорешеваТ.В. Основы системного анализа: Методическое пособие.- СПб: СПбГАСЭ, 2002.
10.Шистеров И.М. Системный анализ: Учебн. пособие. - СПб: СПбГИЭА, 2000.
Дополнительная:
1. Бешелев С.Д., Гуревич Ф.Г. Математико-статистические методы экспертных оценок. - М.: Статистика, 1980.
2. Бондаренко И.Н. Методология системного подхода к решению проблем:история, теория, практика-СПб.: Изд-во СПбУЭФ. 1997.
3. Демченков В.С., Милета В.И. Системный анализ деятельности предприятия. - М.: Финансы и статистика, 1990.
4. Диалектика и системный анализ / Отв. ред. Д. Гвишиани. - М., 1986.
5. Евланов Л.Г., Кутузов В.А Экспертные оценки в управлении. - М.: Экономика, 1978.
6. Ефимов В.М. Имитационная игра для системного анализа управления экономикой. - М., 1988.
7. Карэсев А.И. и др. Математические методы и модели в планировании: Учеб. пос. для экон. вузов - М.: Экономика, 1987.
8. Катков А.Л. Игровая модель выбора перспективных изделий. - Л.: ЛФЭИ, 1981.
9. Кунц Г., О. Доннел С. Управление: системный и ситуационный анализуправленческих функций: Пер. с англ. - М.: Прогресс, 1981.
10. Литвак Б.Г. Экспертная информация: методы получения и анализа. - М: Радио и связь, 1982.
11. ![]() Ногин В.Д., Протодьяконов И.О., Евлампиев ИИ. Основы теории оптимизации: Учебн. пос. - М.: Высш. школа, 1986.
Ногин В.Д., Протодьяконов И.О., Евлампиев ИИ. Основы теории оптимизации: Учебн. пос. - М.: Высш. школа, 1986.
12. Спицнадель В.Н. Основы системного анализа: Учебн. пособие. - СПб: Изд.дом «Бизнес-пресса», 2000
13. Статистическое моделирование и прогнозирование: Учебн. пос. - М.: Финансы и статистика, 1990.
14. Теория систем и методы системного анализа в управлении и связи. В.Н. Волкова, В.А. Воронков, А.А Денисов и др. - М.: Радио и связь, 1983.
16. Ясин Е.Г. Экономическая информация. Методические проблемы. - М.: Наука, 1974.
Приложение 1
Примеры систем
| 1. Автомобиль | 34. Кофемолка | 67. Самолет |
| 2. Ателье | 35. Кухня | 68. Санаторий |
| 3. АТС | 36. Лекция | 69. Сбербанк |
| 4. Аэропорт | 37. Люстра | 70. Светофор |
| 5. Аэрофлот | 38. Магазин | 71. Склад |
| 6. Бензоколонка | 39. Магнитофон | 72. Собрание |
| 7. Библиотека | 40. Мэрия | 73. Спутник |
| 8. Больница | 41. Метро | 74. Стадион |
| 9. Велосипед | 42. Микрофон | 75. Столовая |
| 10. Вентилятор | 43. Министерство | 76. Стройка |
| 11. Вернисаж | 44. Мозг | 77. Суд |
| 12. ВУЗ | 45. Музей | 78. Счеты |
| 13. Газета | 46. Мясорубка | 79. Такси |
| 14. Город | 47. Общежитие | 80. Телевизор |
| 15. Городской транспорт | 48. Общество | 81. Типография |
| 16. Гостиница | 49. Общество потребителей | 82. Трактор |
| 17. Грузовик | 50. Огнетушитель | 83. Транспорт |
| 18. ГЭС | 51. Оранжерея | 84. Трамвай |
| 19. Деканат | 52. Оркестр | 85.Тюрьма |
| 20. Дерево | 53. ОТК | 86. Телефон |
| 21. Детский сад | 54. Отрасль | 87. Учебник |
| 22. Доклад | 55. Очки | 88. Факультет |
| 23. Завод | 56. Парикмахерская | 89. Фотоателье |
| 24. Замок | 57. Пианино | 90. Фотоаппарат |
| 25. Звонок | 58. Планирование | 91. Химчистка |
| 26. Зоопарк | 59. Профсоюз | 92. Хозрасчет |
| 27. Каталог | 60. Птицеферма | 93. Хор |
| 28. Качели | 61. Промышленность | 94. Цех |
| 29. Кинотеатр | 62. Регион | 95. Циркуль |
| 30. Книга | 63. Ректорат | 96. Часы |
| 31. Концерт | 64. Республика | 97. Чемпионат |
| 32. Компьютер | 65. Робот | 98. Швейная машина |
| 33. Кооператив | 66. Рынок | 99. Школа |
| 100. Экономика |
Похожие работы
... , динамические и статические, простые и сложные, естественные и искусственные, с управлением и без управления, непрерывные и дискретные, детерминированные и стохастические, открытые и замкнутые. Основы системного анализа Деление систем на физические и абстрактные позволяет различать реальные системы (объекты, явления, процессы) и системы, являющиеся определенными отображениями (моделями) ре ...
... моделью. Декомпозиция позволяет расчленить всю работу по реализации модели на пакет детальных работ, что позволяет решать вопросы их рациональной организации, мониторинга, контроля и т.д. Агрегирование. В системном анализе процесс, в определенном смысле противоположный декомпозиции – это агрегирование (дословно – соединение частей в целое). Для пояснения его сути приведем такой пример. Допустим, ...
... – это структурный, функциональный, факторный, генетический и временной анализы. Конкретные разновидности аналитической деятельности могут ограничиваться отдельными их разновидностями. Табл. 6. Структура системного анализа Составляющие системного анализа Вид Характеристика Структурный Макроструктурный Выделение системы из среды, определение факторов, которые на нее воздействуют, и того, ...
... подход, этапы системного анализа.[5] Представляется, что в качестве основного процедурного элемента можно рассматривать этапы (процедуры) системного анализа, базирующиеся на целях и принципах системного анализа. 1. Методологические принципы системного анализа Целью анализа системы управления является: · детальное изучение системы управления для более эффективного использования и принятия ...

0 комментариев