Навигация
Рассчитать точечную и интервальную прогнозную оценку с периодом упреждения, равным t = 1
6. рассчитать точечную и интервальную прогнозную оценку с периодом упреждения, равным t = 1.
1)
| t | yt | Скользящая сумма 3 уровней | Скользящая средняя из 3 уровней |
| 1 | 11,9 | - | |
| 2 | 12,6 | 36,7 | 18,35 |
| 3 | 12,2 | 38,7 | 19,35 |
| 4 | 13,9 | 40,4 | 20,2 |
| 5 | 14,3 | 42,8 | 21,4 |
| 6 | 14,6 | 44,2 | 22,1 |
| 7 | 15,3 | 44,3 | 22,15 |
| 8 | 14,4 | 45,5 | 22,75 |
| 9 | 15,8 | 46,9 | 23,45 |
| 10 | 16,7 | 49,9 | 24,95 |
| 11 | 17,4 | 50,2 | 25,1 |
| 12 | 16,1 | - | - |
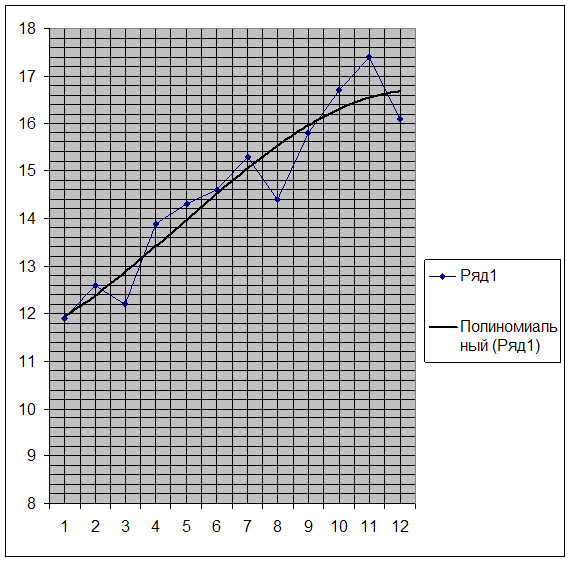
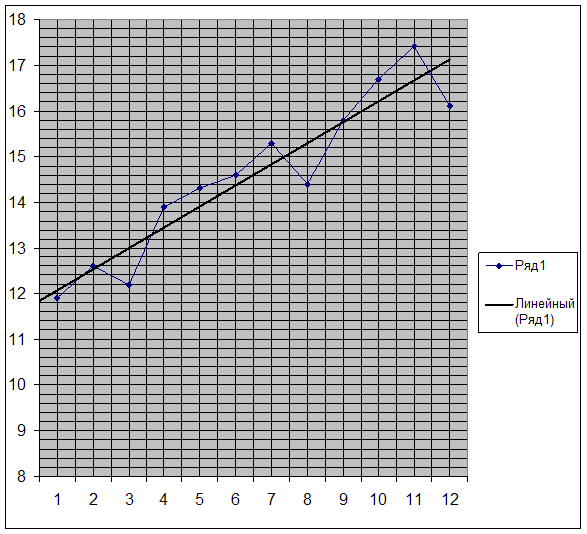
После построения графика (рис. 2) можно сделать вывод о наличии возрастающей тенденции. После построения сглаженного ряда стало более наглядно видно наличие возрастающей тенденции.
2). а) Метод Фостера – Стюарта
| t | Yt | Ut | lt | S | D | Pt |
| 1 | 11,9 | - | - | - | - | - |
| 2 | 12,6 | 1 | 0 | 1 | 1 | 1 |
| 3 | 12,2 | 0 | 0 | 0 | 0 | 1 |
| 4 | 13,9 | 1 | 0 | 1 | 1 | 3 |
| 5 | 14,3 | 1 | 0 | 1 | 1 | 4 |
| 6 | 14,6 | 1 | 0 | 1 | 1 | 5 |
| 7 | 15,3 | 1 | 0 | 1 | 1 | 6 |
| 8 | 14,4 | 0 | 0 | 0 | 0 | 5 |
| 9 | 15,8 | 1 | 0 | 1 | 1 | 8 |
| 10 | 16,7 | 1 | 0 | 1 | 1 | 9 |
| 11 | 17,4 | 1 | 0 | 1 | 1 | 10 |
| 12 | 16,1 | 0 | 0 | 0 | 0 | 9 |
| 175,2 | 8 | 8 | 61 | |||
Выдвинем нулевую гипотезу: во временном ряде (данные графы 2) нет тенденции среднего уровня и нет тенденции дисперсии. Для проверки выдвинутой нулевой гипотезы необходимо рассчитать по формулам 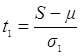 и
и 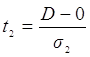 значения t1 и t2. Но для этого надо знать значения μ, σ1,σ2 . В приложении 1 приведены данные для n=10 и для n=15, а нам надо найти данные для n=12.
значения t1 и t2. Но для этого надо знать значения μ, σ1,σ2 . В приложении 1 приведены данные для n=10 и для n=15, а нам надо найти данные для n=12.
Для нахождения данных при n=12 используем принцип интерполяции, предположив, что эти данные в интервале от n=10 до n=15 изменяются линейно, т.е. равномерно. Поэтому нам нужно к значениям данных при n=10 прибавить их изменения за два (2=12–10) шага и получить искомые данных.
Найдем μ для n=12 следующим образом. Значение μ для n=10, согласно приложению 1, равно 3,858. Увеличение μ при изменении n на 2 шага найдем следующим образом
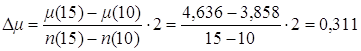 .
.
Отсюда μ(12)=μ(10)+Δμ=3,858+0,311=4,169. Аналогичным образом найдем значения для σ1(12)=1,381 и для σ2(12)=2,040. По формулам (2.7) найдем значения t1 и t2
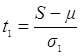 = (8 – 4,169)/1,381 = 3,326;
= (8 – 4,169)/1,381 = 3,326; 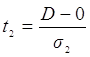 = (8-0)/2,040 = 3,92
= (8-0)/2,040 = 3,92
Случайные величины t1 и t2 имеют распределение Стьюдента с числом степеней свободы К = n – 1 = 12 – 1 = 11 и уровнем значимости a, который может принимать значения 0,01; 0,05 и т.д. Примем уровень значимости (вероятность, с которой исследователь может ошибиться), равный 0,05 (5%). На основе выбранного уровня значимости а = 0,05 рассчитаем доверительную вероятность: g = 1 – а = 1 – 0,05 = 0,95.
По числу степеней свободы К = 11 и величине доверительной вероятности g = 0,95 по таблице «Значение t-критерия Стьюдента» (Приложение 1)определим табличное значение случайной величины (tg): tg = 2,201.
Расчетные значения t1 и t2 сопоставим с табличным tg.
Если сопоставить расчетные значения t1 и t2 с табличным tg, то может возникнуть четыре ситуации.
1) |t1| > |tg|.
Данный вариант означает, что нулевая гипотеза об отсутствии в ряде тенденции отвергается и с вероятностью g во временном ряде имеет место тенденция дисперсии.
2) |t1| < |tg|.
Данный вариант означает, что нулевая гипотеза об отсутствии в ряде тенденции принимается и с вероятностью g во временном ряде нет тенденции дисперсии.
3) |t2| > |tg|.
Данный вариант означает, что нулевая гипотеза об отсутствии в ряде тенденции отвергается и с вероятностью g во временном ряде имеет место тенденция в среднем.
4) |t2| < |tg|.
Данный вариант означает, что нулевая гипотеза об отсутствии в ряде тенденции принимается и с вероятностью g во временном ряде нет тенденции в среднем.
1) 3,326 > 2,201; 3,92 > 2,201Þ нулевая гипотеза об отсутствии в ряде тенденции отвергается и с вероятностью g = 0,95 можно говорить, что во временном ряде имеет место тенденция дисперсии
б) Метод коэффициента Кенделла
Определим расчетное значение коэффициента Кендэла (tр):
| tр = | 4 × р | – 1, |
| n × (n – 1) |
где n – количество уровней во временном ряде.
| tр = | 4 × 61 | – 1 = 0,85 |
| 12 × (12 – 1) |
Коэффициент Кендэла является случайной величиной, соответствует нормальному распределению и изменяется от -1 до +1. Теоретическими характеристиками коэффициента Кендэла являются математическое ожидание, которое равно нулю (Мt = 0) и дисперсия, рассчитываемая по формуле:
| st2 = | 2 × (2 × n + 5) | . |
| 9 × n × (n – 1) |
| st2 = | 2 × (2 × 12 + 5) | = | 58 | = 0,049 |
| 9 × 12 × (12 – 1) | 1188 |
Если сопоставить расчетное и теоретическое значение коэффициента Кендэла, то может возникнуть три ситуации.
1) (0 – td ×![]() ) < tр < (0 + td ×
) < tр < (0 + td ×![]() ),
),
где td – коэффициент доверия.
Данный вариант означает, что с вероятностью td во временном ряде нет тренда.
2) tр < (0 – td ×![]() )
)
Данный вариант означает, что с выбранной вероятностью в ряде имеет место убывающая тенденция.
3) tр > (0 + td ×![]() )
)
Данный вариант означает, что с выбранной вероятностью в ряде имеет место возрастающая тенденция.
При выбранной вероятности 0,95 (95%) коэффициент доверия td = 1,96.
tр > (0 + 1,96 × ![]() )
)
0,85 > + 0,434
Таким образом, с вероятностью 0,95 (95%) можно говорить о наличии в ряде возрастающей тенденции в среднем (тренда).
В ходе анализа временного ряда на наличие в нем тенденции среднего уровня (тренда) по методу Фостера – Стюарта и методу коэффициента Кенделла получены аналогичные результаты. Следовательно, в ряде отмечается возрастающая тенденция в среднем.
Таким образом, визуальная оценка нашла свое подтверждение в ходе аналитических расчетов с использованием соответствующих методов оценки временного ряда на наличие в нем тенденции.
3). Метод усреднения по левой и правой половине
Метод усреднения по левой и правой половине - графический метод, используется для нахождения параметров линейного тренда.
Для нахождения параметров а0 и а1 разделим исходные данные пополам и по каждой половине рассчитаем средние значения фактора и уровня ряда.
|
| 1 + 2 + 3 + 4 + 5 + 6 | = 3,5 |
| 6 |
|
| 11,9 + 12,6 + 12,2 + 13,9 + 14,3 + 14,6 | = 13,25 |
| 6 |
|
| 7 + 8 + 9 + 10 + 11 + 12 | = 9,5 |
| 6 |
|
| 15,3 + 14,4 + 15,8 + 16,7 + 17,4 + 16,1 | = 15,95 |
| 6 |
В результате расчетов получили две точки: А (3,5; 13,25), В (9,5; 15,95).
Построим графическую модель исходного временного ряда и найдя точки А и В, проведем через них прямую, которая будет отображать тенденцию исходного временного ряда (рис. 3).
|
Рис. 3. Еженедельный оборот магазина «Ткани для дома» (исходный ряд и линейный тренд)
Из графика видно, что построенный линейный тренд отражает тенденцию исходного ряда: возрастающий тренд.
Для нахождения параметра а0 продолжим линию до пересечения с осью ординат. Чтобы найти параметр а1, преобразуем уравнение тренда:
а1t = ![]() – а0 | :t
– а0 | :t
| а1 = |
|
| t |
Зададимся произвольным значение параметра t (например, t = 3,5). По графику модели найдем значение параметра а0 (а0 = 13,45). Рассчитаем значение параметра а1.
| а1 = | 13,25 – 11,8 | = 0,41 |
| 3,5 |
Таким образом, уравнение линейного тренда будет иметь следующий конкретный вид:
![]() = 11,8+ 0,41t.
= 11,8+ 0,41t.
4). Расчет параметров линейного тренда ![]() t= а0 + а1t по исходным данным методом МНК.
t= а0 + а1t по исходным данным методом МНК.
| t | y | t2 | yt |
| 1 | 11,9 | 1 | 11,9 |
| 2 | 12,6 | 4 | 25,2 |
| 3 | 12,2 | 9 | 36,6 |
| 4 | 13,9 | 16 | 55,6 |
| 5 | 14,3 | 25 | 71,5 |
| 6 | 14,6 | 36 | 87,6 |
| 7 | 15,3 | 49 | 107,1 |
| 8 | 14,4 | 64 | 115,2 |
| 9 | 15,8 | 81 | 142,2 |
| 10 | 16,7 | 100 | 167 |
| 11 | 17,4 | 121 | 191,4 |
| 12 | 16,1 | 144 | 193,2 |
| 78 | 175,2 | 650 | 1204,5 |
Для нахождения параметров строится система нормальных уравнений.
 =(175,2*650-78*1204,5)/(12*650-78*78)=11,614;
=(175,2*650-78*1204,5)/(12*650-78*78)=11,614;
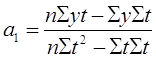 =(12*1204,5-175,2*78)/(12*650-78*78)=-0,459
=(12*1204,5-175,2*78)/(12*650-78*78)=-0,459
Расчет параметров параболического тренда ![]() t= а0 + а1t + a2t2 по исходным данным методом МНК.
t= а0 + а1t + a2t2 по исходным данным методом МНК.
| t | y | t2 | yt | t4 | yt2 | t3 |
| 1 | 11,9 | 1 | 11,9 | 1 | 11,9 | 1 |
| 2 | 12,6 | 4 | 25,2 | 16 | 50,4 | 8 |
| 3 | 12,2 | 9 | 36,6 | 81 | 109,8 | 27 |
| 4 | 13,9 | 16 | 55,6 | 256 | 222,4 | 64 |
| 5 | 14,3 | 25 | 71,5 | 625 | 357,5 | 125 |
| 6 | 14,6 | 36 | 87,6 | 1296 | 525,6 | 216 |
| 7 | 15,3 | 49 | 107,1 | 2401 | 749,7 | 343 |
| 8 | 14,4 | 64 | 115,2 | 4096 | 921,6 | 512 |
| 9 | 15,8 | 81 | 142,2 | 6561 | 1279,8 | 729 |
| 10 | 16,7 | 100 | 167 | 10000 | 1670 | 1000 |
| 11 | 17,4 | 121 | 191,4 | 14641 | 2105,4 | 1331 |
| 12 | 16,1 | 144 | 193,2 | 20736 | 2318,4 | 1728 |
| 78 | 175,2 | 650 | 1204,5 | 60710 | 10322,5 | 6084 |
Для нахождения параметров строится система нормальных уравнений.
![]() na0 + a1St + a2St2 = Sy;
na0 + a1St + a2St2 = Sy;
a0St + a1St2 + a2St3 = Syt;
a0St2 + a1St3 + a2St4 = Syt2.
| а0 = | Sy St2 St4 + St St3 Syt2 + Syt St3 St2 – St Syt St4 – St3 St3 Sy – St2 St2 Syt2 | . |
| n St2 St4 + St St3 St2 + St St3 St2 – St2 St2 St2 – St3 St3 n – St St St4 |
| а0 = | 175,2 × 650 × 60710 + 78 × 6084 × 10322,5 + 1204,5 × 6084 × 650 – 78 × 1204,5 × 60710 – |
| 12 × 650 × 60710 + 78 × 6084 × 650 + 78 × 6084 × 650 – 650 × 650 × 650 – |
| – 6084 × 6084 × 175,2 – 650 × 650 × 10322,5 | = 11,12. |
| – 6084 × 6084 × 12 – 78 × 78 × 60710 |
| а1 = | n Syt St4 + St Syt2 St2 + Sy St3 St2 – St2 Syt St2 – Syt2 St3 n – Sy St St4 | . |
| n St2 St4 + St St3 St2 + St St3 St2 – St2 St2 St2 – St3 St3 n – St St St4 |
| а1 = | 12 × 1204,5 × 60710 + 78 × 10322,5 × 650 + 175,2 × 6084 × 650 – 650 × 1204,5 × 650 – |
| 12 × 650 × 60710 + 78 × 6084 × 650 + 78 × 6084 × 650 – 650 × 650 × 650 – |
| – 10322,5 × 6084 × 12 – 175,2 × 78 × 60710 | = 0,67. |
| – 6084 × 6084 × 12 – 78 × 78 × 60710 |
| а2 = | n St2 Syt2 + St St3 Sy + St Syt St2 – Sy St2 St2 – Syt St3 n – St St Syt2 | . |
| n St2 St4 + St St3 St2 + St St3 St2 – St2 St2 St2 – St3 St3 n – St St St4 |
| а2 = | 12 × 650 × 10322,5 + 78 × 6084 × 175,2 + 78 × 1204,5 × 650 – 175,2 × 650 × 650 – |
| 12 × 650 × 60710 + 78 × 6084 × 650 + 78 × 6084 × 650 – 650 × 650 × 650 – |
| – 1204,5 × 6084 × 12 – 78 × 78 × 10322,5 | = -0,016. |
| – 6084 × 6084 × 12 – 78 × 78 × 60710 |
Таким образом, параболический тренд имеет следующий вид:
![]() t= 11,12 + 0,67 × t - 0,016 × t2.
t= 11,12 + 0,67 × t - 0,016 × t2.
![]()
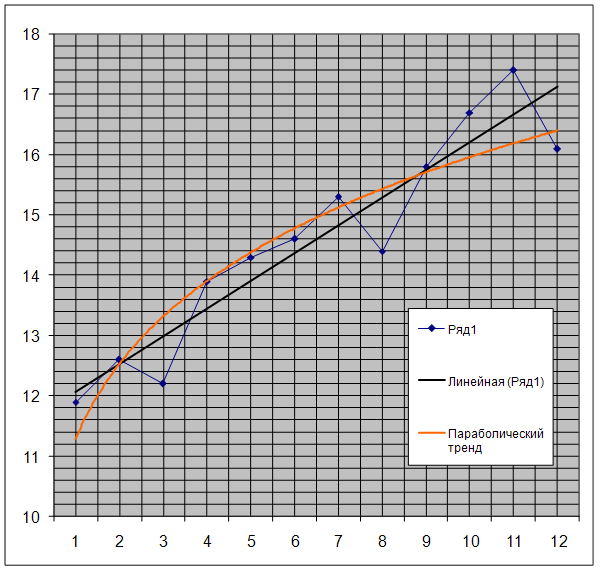
Рис. 4. Еженедельный оборот магазина «Ткани для дома» (исходный ряд, линейный и параболический тренд)
Проведем оценку аппроксимации линейного тренда и выбранной параболической трендовой модели с помощью критерия наименьшей суммы квадратов отклонений, который имеет следующий вид:
| S = | S(yt – | Þ min |
| n – m |
где n – количество уровней ряда; m – число параметров трендовой модели.
| t | yt | Линейный | Параболический | ||
|
| (yt – |
| (yt – | ||
| 1 | 11,9 | 12,21 | 0,0961 | 11,774 | 0,015876 |
| 2 | 12,6 | 12,62 | 0,0004 | 12,396 | 0,041616 |
| 3 | 12,2 | 13,03 | 0,6889 | 12,986 | 0,617796 |
| 4 | 13,9 | 13,44 | 0,2116 | 13,544 | 0,126736 |
| 5 | 14,3 | 13,85 | 0,2025 | 14,07 | 0,0529 |
| 6 | 14,6 | 14,26 | 0,1156 | 14,564 | 0,001296 |
| 7 | 15,3 | 14,67 | 0,3969 | 15,026 | 0,075076 |
| 8 | 14,4 | 15,08 | 0,4624 | 15,456 | 1,115136 |
| 9 | 15,8 | 15,49 | 0,0961 | 15,854 | 0,002916 |
| 10 | 16,7 | 15,9 | 0,64 | 16,22 | 0,2304 |
| 11 | 17,4 | 16,31 | 1,1881 | 16,554 | 0,715716 |
| 12 | 16,1 | 16,72 | 0,3844 | 16,856 | 0,571536 |
| - | - | 173,58 | 4,483 | 175,3 | 3,567 |
Для линейного тренда
| S = | 4,483 | = 0,4483. |
| 12 – 2 |
Для параболического тренда
| S = | 3,567 | = 0,396. |
| 12 – 3 |
0,4483 > 0,396; Þ параболическая модель наилучшим образом аппроксимирует исходный временной ряд.
5)
| t | yt |
| et | Pt | et2 | (et – | (et – et-1) 2 |
| 1 | 11,9 | 12,21 | -0,31 | – | 0,0961 | 0,198025 | – |
| 2 | 12,6 | 12,62 | -0,02 | 1 | 0,0004 | 0,024025 | 0,166 |
| 3 | 12,2 | 13,03 | -0,83 | 1 | 0,6889 | 0,931225 | 0,107 |
| 4 | 13,9 | 13,44 | 0,46 | 1 | 0,2116 | 0,105625 | 0,200 |
| 5 | 14,3 | 13,85 | 0,45 | 0 | 0,2025 | 0,099225 | 0,870 |
| 6 | 14,6 | 14,26 | 0,34 | 1 | 0,1156 | 0,042025 | 0,045 |
| 7 | 15,3 | 14,67 | 0,63 | 1 | 0,3969 | 0,245025 | 0,000 |
| 8 | 14,4 | 15,08 | -0,68 | 1 | 0,4624 | 0,664225 | 0,529 |
| 9 | 15,8 | 15,49 | 0,31 | 0 | 0,0961 | 0,030625 | 0,306 |
| 10 | 16,7 | 15,9 | 0,8 | 0 | 0,64 | 0,442225 | 0,111 |
| 11 | 17,4 | 16,31 | 1,09 | 1 | 1,1881 | 0,912025 | 1,182 |
| 12 | 16,1 | 16,72 | -0,62 | – | 0,3844 | 0,570025 | 0,352 |
| S | 175,2 | 173,58 | 1,62 | 7 | 4,483 | 4,2643 | 3,868 |
Найдем величины случайных отклонений для исходного ряда по формуле: et = yt – ![]() t.
t.
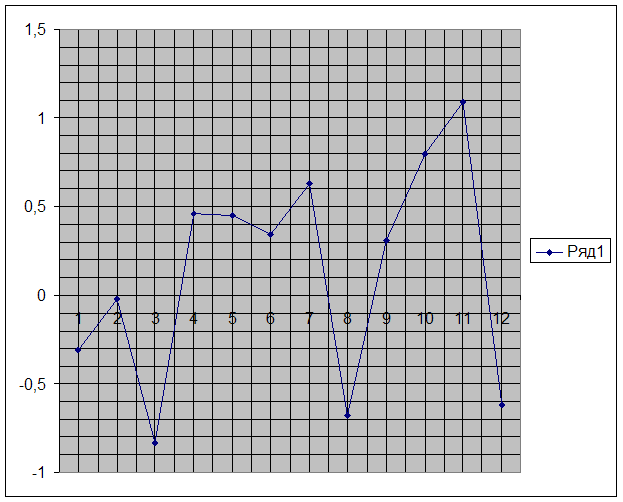
Построим график ряда отклонений et (рис. 5).
|
Рис. 5. График ряда отклонений et
Из графика видно, что в ряде отклонений et отсутствует тенденция.
Оценим адекватность выбранной трендовой модели (параболы) исходному ряду на основе анализа ряда отклонений et.
1) Колебание величины et носит случайный характер. Выполнение этого условия означает, что величина et не содержит элементов тренда. Проверим это условие с помощью критерия поворотных точек. Точка считается поворотной, если выполняется одно из следующих условий:
et-1 < et > et+1
et-1 > et < et+1
Обозначим поворотные точки как Рt = 1. В противном случае Pt = 0. Найдем сумму всех поворотных точек P = SPt.
Выдвинем нулевую гипотезу – Н0: колебание величины et носит случайный характер. Для проверки нулевой гипотезы рассчитаем математическое ожидание и дисперсию поворотных точек.
| М(Р) = | 2 (n – 2) | = | 2 × (12 – 2) | = 6,667. |
| 3 | 3 |
| D(Р) = | 16 n – 29 | = | 16 × 12 – 29 | = 1,811. |
| 90 | 90 |
При вероятности 0,95 (95%) коэффициент доверия td = 1,96.
Если расчетное значение числа поворотных точек попадает в интервал
(М(Р) – td![]() ) < P < (М(Р) + td
) < P < (М(Р) + td![]() ), то с выбранной вероятностью можно утверждать, что колебания величины et носит случайный характер.
), то с выбранной вероятностью можно утверждать, что колебания величины et носит случайный характер.
(6,667 – 1,96 ![]() ) < 7 < (6,667 + 1,96
) < 7 < (6,667 + 1,96 ![]() )
)
4,029 < 7 < 9.305
Таким образом, с вероятностью 95% можно утверждать, что колебания величины et носит случайный характер.
2) Распределение величины etсоответствует нормальному распределению. Для этого используем RS-критерий.
S![]() =
= ![]() =
=![]() = 0,706
= 0,706
| RSр = | emax – emin | = | 1.09– (- 0,83) | = 2,777. |
| S | 0,706 |
Определим табличное значение RS-критерия по таблице «Значения RS-критерия для n от 10 до 30» (Приложение 3).
| RS12Н = 2,67 + 2 × | 3,18 – 2,67 | = 2,772 |
| 20 – 10 |
| RS12В = 3,85 + 2 × | 4,49 – 3,85 | = 3,978 |
| 20 – 10 |
Выдвинем нулевую гипотезу: величина et соответствует нормальному распределению. Для этого должно выполняться условие: RS12Н < RSр < RS12В.
Поскольку это условие выполняется (2,772 < 2,777 < 3,978), то с вероятность 0,95 (95%) можно утверждать, что распределение величины et соответствует нормальному распределению.
3) Математическое ожидание величины et равно нулю. Для проверки этого условия выдвинем нулевую гипотезу – Н0: М(et) = 0, после чего определим расчетное значение величины tр:
| tр = |
| × |
| Se |
где ![]() – средняя арифметическая простая величины et; Se – среднее квадратическое отклонение величины et.
– средняя арифметическая простая величины et; Se – среднее квадратическое отклонение величины et.
|
| Set | = | 1.62 | = 0,135 |
| n | 12 |
Se= ![]() =
=![]() = 0,623
= 0,623
| tр = | 0,135 – 0 | × |
| 0,623 |
Найдем табличное значение tт (Приложение 1) по распределению Стьюдента при доверительной вероятности g = 1 – а = 1 – 0,05 = 0,95 и числе степеней свободы К = n – 1 = 12 – 1 = 11. В данном случае tт = 2,201.
Сопоставим табличное и расчетное значения. Если th < tт, то нулевая гипотеза принимается, и наоборот.
0,75 < 2,201, Þ с вероятностью 0,95 (95%) принимается нулевая гипотеза, т.е. М(et) = 0.
4) Независимость членов ряда между собой (проверка временного ряда на отсутствие автокорреляции). Для проверки данного условия используется критерий Дарбина – Уотсона, расчетное значение которого определяется следующим образом:
| dр = | S(et – et-1) 2 | = | 8,4451 | = 1,88. |
| S et2 | 4,483 |
dр¢ = 4 – 1,88 = 2,12.
По таблице «Распределение критерия Дарбина – Уотсона» для положительной автокорреляции (для 5% уровня значимости)» находим табличное значение dт. При n = 12 и V = 1 нижнее и верхнее значения распределения будут соответственно равны d1 = 1,08 и d2 = 1,36.
Сравним расчетное и табличное значения: dр > d2 (2,12 > 1,36). Таким образом, с вероятностью 95% можно говорить об отсутствии в ряде автокорреляции.
6). Рассчитаем точечную прогнозную оценку с периодом упреждения t = 1 для линейного тренда (![]() t= 11,614+ 0,459× t):
t= 11,614+ 0,459× t):
![]() (n+t) = а0 + а1 × (n+t);
(n+t) = а0 + а1 × (n+t);
![]() (12+1) = 11,614+ 0,459× (12 + 1) = 17,581.
(12+1) = 11,614+ 0,459× (12 + 1) = 17,581.
Интервальный прогноз для линейного тренда:
![]() (n+t) =
(n+t) =![]() (n+t) + tт × S
(n+t) + tт × S![]() ×
×  ,
,
где n – число уровней ряда в периоде основания прогноза; t - период упреждения прогноза; tт – табличное значение по Стьюденту с уровнем значимости (а) и числом степеней свободы (К = n - 2); S![]() – стандартная ошибка тренда.
– стандартная ошибка тренда.
tт ×  = К¢; Þ
= К¢; Þ ![]() (n+t) =
(n+t) =![]() (n+t) + S
(n+t) + S![]() × К¢.
× К¢.
При t = 1 и n = 12 по таблице «Значение К для оценки доверительных интервалов прогноза при вероятности g = 0,9 (линейный тренд)» (Приложение 6) К¢ = 2,1274.
S![]() =
= ![]() =
=![]() = 0,67.
= 0,67.
Интервальный прогноз для линейного тренда
![]() (12+1) = 17,581 + 0,67 × 2,1274=19,0064
(12+1) = 17,581 + 0,67 × 2,1274=19,0064
![]() (12+1) = 17,581 - 0,67 × 2,1274=16,1556
(12+1) = 17,581 - 0,67 × 2,1274=16,1556
16,1556 < ![]() 13 < 19,0064, т.е. с вероятностью 0,9 (90%) можно утверждать, что на 13-ый день оборот магазина «Ткани для дома» составит от 16,1556 до 19,0064 д.е.
13 < 19,0064, т.е. с вероятностью 0,9 (90%) можно утверждать, что на 13-ый день оборот магазина «Ткани для дома» составит от 16,1556 до 19,0064 д.е.
![]() t= 11,12 + 0,67 × t - 0,016 × t2.
t= 11,12 + 0,67 × t - 0,016 × t2.
Рассчитаем точечную прогнозную оценку с периодом упреждения t = 1 для параболического тренда (![]() t= 11,12 + 0,67 × t - 0,016 × t2):
t= 11,12 + 0,67 × t - 0,016 × t2):
![]() (n+t) = а0 + а1 × (n+t) + а2 × (n+t)2;
(n+t) = а0 + а1 × (n+t) + а2 × (n+t)2;
![]() 13 = 11,12 + 0,67 × 13 - 0,016 × 132 = 17,126.
13 = 11,12 + 0,67 × 13 - 0,016 × 132 = 17,126.
Интервальный прогноз для нелинейного (параболического) тренда:
![]() (n+t) =
(n+t) =![]() (n+t) + S
(n+t) + S![]() × К¢.
× К¢.
При t = 1 и n = 12 по таблице «Значение К для оценки доверительных интервалов прогноза при вероятности g = 0,9 (параболический тренд)» (Приложение 7) К¢ = 2,636.
S![]() =
= ![]() =
=![]() = 0,63.
= 0,63.
Интервальный прогноз для нелинейного (параболического) тренда
![]() 13 = 17,126 + 0,63 × 2,636=18,7867
13 = 17,126 + 0,63 × 2,636=18,7867
![]() 13 = 17,126 - 0,63 × 2,636=15,4653
13 = 17,126 - 0,63 × 2,636=15,4653
15,4653 < ![]() 13 < 18,7867, т.е. с вероятностью 0,9 (90%) можно утверждать, что на 13-ый день оборот магазина «Ткани для дома» составит от 15,4653 до 18,7867 д.е.
13 < 18,7867, т.е. с вероятностью 0,9 (90%) можно утверждать, что на 13-ый день оборот магазина «Ткани для дома» составит от 15,4653 до 18,7867 д.е.
Похожие работы
... , процентные ставки, размеры банковских депозитов, валютные курсы. Основной характеристикой конъюнктуры рынка является степень сбалансированности спроса и предложения. Она проявляется в поведении цен, скорости оборачиваемости товаров. Эта оценка позволяет определять тип конъюнктуры. 2. Маркетинговая логистика: понятия, цели, функции, задачи менеджмента по координации товародвижения. Концепция ...
... + 15 + 16,6 = 58,9 Таким образом в условиях оптим. Рынка ориентация будет на реализацию стир. машин. 5 билет Вопрос 1: Основные направления маркетинговых исследований: 1. Исследование характеристик рынка 2. Исследование внутренних потенциальных возможностей производственной или посреднической деятельности предприятия / фирмы. Процесс маркетинговых исследований и его характеристика: ...
... . Гражданам, задействованным во временных работах, пособие по безработице выдается полностью и без задержек.[16]. 3. Проблемы и пути их решения. Главной проблемой на рынке труда по прежнему остается безработица, т.е. трудоустройство граждан (безработных) затруднено дефицитом вакансий, заявленных предприятиями и организациями в службу ...
... отдел; Управление материально-техническим снабжением; Управление рабочего снабжения; Торговый отдел; Цех автоперевозок; Железнодорожный цех. Для того чтобы, рассмотреть, как организованна коммерческая деятельность на ОАО «СТЗ», нужно рассмотреть, чем занимаются подразделения блока, взаимодействие между ними и подразделениями других блоков. Заместитель директора по сбыту контролирует отдел ...
0 комментариев