Навигация
Речь идёт о процессе движения, которое характеризуется тремя величинами: расстояние, скорость, время (3 столбца таблицы)
1. Речь идёт о процессе движения, которое характеризуется тремя величинами: расстояние, скорость, время (3 столбца таблицы).
2. В задаче 3 процесса: движение скорого, пассажирского и товарного поездов (3 строчки таблицы).
Можно составить «скелет» таблицы.
| Величины Процессы | Расстояние (км) | Скорость (км/ч) | Время (ч) |
| Скорый поезд | |||
| Пассажирский поезд | |||
| Товарный поезд |
3. Заполняем таблицу в соответствии с условиями задачи
4. Вводим неизвестные величины: x, км/ч – скорость товарного поезда, y, ч – время движения скорого поезда.
5. Составим «модель».
(x+50)y = 8/5 x(y+1)
8/5 x(y+1) = x(y+4)
6. Решаем эту систему. Из первого уравнения находим у. Из второго уравнения находим х.
Решение задачи (чистовик).
Пусть х, км/ч – скорость товарного поезда (х>0), у, ч – время движения скорого поезда (у>0).
Составляем таблицу.
| Величины Процессы | Расстояние (км) | Скорость (км/ч) | Время (ч) |
| Скорый поезд | (х+50)у | х+50 ? | у |
| Пассажирский поезд | 8/5 х(у+1) | 8/5 х | у+1 |
| Товарный поезд | х(у+4) | х ? | у+4 |
По условию задачи поезда прошли одно и то же расстояние. Получаем систему уравнений
8/5 х(у+1) = х(у+4)
(х+50)у = х(у+4).
По условию задачи х>0, тогда
8(у+1) = 5(у+4)
(х+50)у = х(у+4),
3у = 12
(х+50)у = х(у+4),
у = 4
х+50 = 2х,
у = 4
х = 50.
Полученные значения неизвестных удовлетворяют условию х>0, у>0, значит удовлетворяют условию задачи.
50 км/ч – скорость товарного поезда.
50+50 = 100 (км/ч) – скорость скорого поезда.
Проверка по условию задачи.
50 км/ч – скорость товарного поезда,
4+4 = 8 (ч) – время движения товарного поезда.
50*8 = 400 (км) – расстояние, которое прошёл товарный поезд.
50*8/5 = 80 (км/ч) – скорость пассажирского поезда.
4+1 = 5 (ч) – время движения пассажирского поезда.
80*5 = 400 (км) – расстояние, которое прошёл пассажирский поезд.
4 ч – время движения скорого поезда.
50+50 = 100 (км/ч) – скорость скорого поезда.
100*4 = 400 (км) – расстояние, которое прошёл скорый поезд.
Каждый поезд прошёл одно и то же расстояние.
Задача решена верно.
Ответ: 50 км/ч, 100 км/ч.
Аналогично можно решать задачи «на работу», «наполнение бассейна».
Приложение 2.
Урок «Составление алгоритма алгебраического способа решения задач»
Цель:
1. Исследование алгебраического способа решения задач и составление алгоритма.
2. Формирование действия моделирования.
3. Развитие компонентов УД.
Оборудование:
1. Карточки:
- арифметический способ решения;
- алгебраический способ решения;
- задача.
2. Фломастеры, мелки, чистые листы, магниты, компьютеры.
3. Учебные принадлежности.
Ход урока
Организационный момент:
Чему учимся на уроке математики?
Что уже знаем хорошо?
Чему надо учиться?
Тему урока сформулируем позже.
Откроем тетради, оформим начало работы.
Актуализация:
1. Вспомним некоторые умения, которые помогут в дальнейшем.
Индивидуальная работа - Составить по схеме уравнения и записать их.
| Х | 5 | ||
| 5 | 20 | 72 | |
(3· х+5· 2+20=72)
Все остальные учащиеся выполняют любое из этих заданий:
Запиши уравнения и реши их.
1. Число 40 увеличили на произведение числа 6 и неизвестного и получили 76.
2. Составьте уравнение и решите задачи.
В классе 28 учеников. Сколько мальчиков в классе, если девочек 13?
В трех вазах 27 гвоздик. В первой вазе на 3 гвоздики меньше, чем во второй вазе, и на 6 гвоздик больше, чем в третьей. Сколько гвоздик в третьей вазе?
1.187 * (33467 : 49 – 362)
Что мы должны знать об уравнении?
Для чего нужны уравнения?
2. Построение моделей к уравнениям выполняем неплохо.
Вспомним, как они решаются.
Нам поможет компьютер.
Сели за компьютер. Задания выполняем в уме.
Порядок работы:
а) Прочитай информацию.
б) Подумай, а потом выполняй.
Какие инструменты нам необходимы:
а) экран
б) мышка
в) калькулятор
г) резинка
в конце посмотреть результаты, сравнить с прошлым.
(Даются 11 заданий: сложные уравнения на : и х в пределах 100)
Кто закончил на черновике, составляет уравнения с числами а, 8, 32, 4.
3. Нам необходимо еще вспомнить одно умение.
(арифметический способ решения задач на листочках.)
Задача. В трех одинаковых ящиках 21 кг апельсинов. Сколько апельсинов в 8 таких же ящиках?
Работаем в паре.
Модель, решение. (Можно записать выражением, можно по действиям.)
Проверяем.
Чем пользовались?
Составление алгоритма алгебраического способа решения задач.
Постановка учебной задачи.
Скажите, а можно было решить эту задачу другим способом?
Что нужно иметь для решения алгебраическим способом?
А он есть у нас?
А может ли его составить?
Да, мы с вами уже решали задачи таким способом.
Скажите, а есть ли подсказка к составлению алгоритма?
Составляем алгоритм, записываем на листочках. Работаем в группах.
Определите, кто будет записывать, кто рассказывать.
Кто закончит, прикрепляем алгоритм на доску.
Вместе будем выбирать пункты алгоритма.
Идет самостоятельная работа по составлению алгоритма.
Проверка работы.
Алгоритм:
1. Чтение задачи.
2. Выделение известных и неизвестных величин.
3. Установление связи между условием и вопросом.
4. Моделирование.
5. Введение неизвестного.
6. Выражение через это неизвестное других величин.
7. Установление равенства.
8. Составление уравнения.
9. Решение уравнения.
10. Формулировка ответа.
11. Проверка.
Решение задачи способом уравнения.
Вернемся к нашей задаче, решим ее уравнением.
Х кг – в 8 ящиках
(21 : 3) кг – масса одного ящика из 3
(Х : 8) кг – масса одного ящика из 8
Уравнение: 21 : 3 = Х : 8
Упрощаем: Х : 8 = 7
Х = 56 (кг)
Ответ: 56 кг в 8 ящиках.
Какая тема урока сегодня? (Формулируем тему совместно).
(«Составление алгоритма алгебраического способа решения задач»).
Итог урока.
[1] Паламарчук В.Ф. Школа учит мыслить. - М.: Просвещение, 1987. С. 22.
[2] Фридман Л.М., Турецкий Е.Н. Как научиться решать задачи. - М.: Просвещение, 1984. С. 12.
[3] Виноградова Л.П. Обучение решению задач // Фестиваль педагогических идей «Открытый урок». – М.: Первое сентября, 2004. С. 29.
[4] Петухова Л.И. О решении текстовых задач по математике // Фестиваль педагогических идей «Открытый урок». – М.: Первое сентября, 2004. С. 34.
[5] Чаплыгин В.Ф. Некоторые методические соображения по решению текстовых задач // Математика в школе. – 2000. - №4. - С.28.
[6] Чаплыгин В.Ф. Некоторые методические соображения по решению текстовых задач // Математика в школе. – 2000. - №4. - С.29.
[7] Чаплыгин В.Ф. Некоторые методические соображения по решению текстовых задач // Математика в школе. – 2000. - №4. - С. 29.
[8] Левитас Г.Г. Об алгебраическом решении текстовых задач // Математика в школе. – 2000. - №8. - С. 13.
[9] Лебедев В. Анализ и решение текстовых задач // Математика в школе. – 2002. - №11. - С. 8.
[10] Епишева О.Б. Общая методика преподавания математики в средней школе: Курс лекций. - Тобольск: Изд. ТГПИ им. Д.И.Менделеева, 1997. С. 56.
Похожие работы
... в том, что с помощью с сюжетных задач обучаемый может познавать реальную действительность, осознавать те знания и умения, которые необходимы при решении любых задач, а не только сюжетных. 1.3 Методика обучения решению сюжетных задач в курсе математики 5-6 классов Сюжетной задачей называют такую задачу, в которой данные и связь между ними включены в фабулу. Содержание сюжетной задачи чаще ...
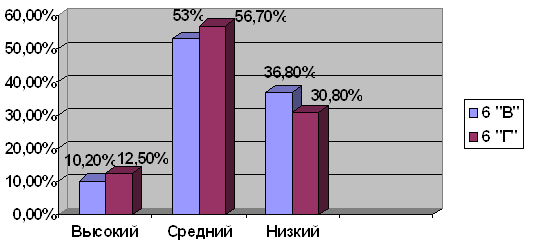
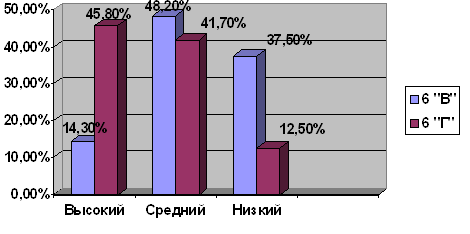
... и перенести полученные знания на практику. Глава 2. Работа учителя по развитию логического мышления на уроках математики 2.1 Опытно-экспериментальная работа и анализ ее результатов Опытно-экспериментальное исследование по выявлению уровня развития логического мышления школьников при решении текстовых задач проводилось на базе МОУ «Средняя общеобразовательная школа № 10» г. Кунгура в ...
... на качественно новую ступень овладения содержанием школьной математики. Глава II. Методико - педагогические основы использования самостоятельной работы, как средство обучения решению уравнений в 5 - 9 классах. § 1. Организация самостоятельной работы при обучения решению уравнений в 5 - 9 классах. При традиционном способе преподавания учитель часто ставит ученика в положение объекта ...
... выдвинутой гипотезы на базе школы № 24 был проведен психолого-педагогический эксперимент, цель которого: изучить специфические особенности и пути усовершенствования процесса обучения школьников решению составных задач. Задачи экспериментальной части исследования: - Рассмотрев известные, но мало применяемые на практике способы работы над составной задачей, включить их в практическую работу с ...
0 комментариев