Навигация
Вычислить, используя формулу разности квадратов, 31*29
5. Вычислить, используя формулу разности квадратов, 31*29.
6. К выражению х2 + рх прибавить такое слагаемое, чтобы получился квадрат суммы.
Игра «лабиринт». 7 класс.
Эта игра — нетрадиционная форма проведения урока контроля знаний. Ее можно проводить после изучения любой темы (здесь, для примера, взята тема курса алгебры VII класса «Сумма и разность многочленов. Произведение одночлена на многочлен»). Игра рассчитана на один урок и предполагает индивидуальную форму работы. Каждый игрок получает комплект, состоящий из схемы Лабиринта, таблиц «Стоимость задач» и «Критерии оценки», карточку с заданиями.
Правила игры
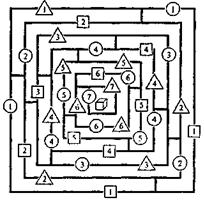
Задача игрока — добраться до сундука с сокровищами, находящегося в центре Лабиринта. Для этого необходимо пройти семь ворот Лабиринта — выполнить семь заданий (на схеме ворота обозначены цифрами со значком, символизирующим уровень сложности задания).
На каждом этапе надо решить задачу определенного типа, при этом задачи одного типа отличаются уровнем сложности (всего их три) и имеют разную стоимость, выраженную в баллах (см. таблицу «Стоимость задач»). Все задания определены таким образом, что среди семи обязательно попадутся задачи разного уровня сложности.
Путь по Лабиринту каждый игрок определяет самостоятельно, выбирая оптимальный для себя уровень сложности заданий. Войти в Лабиринт можно через любые ворота и дальше продвигаться только к его центру.
Решения всех выбранных задач записываются на отдельном листе, а уровень сложности отмечается соответствующим значком.
Оценка за работу выставляется в соответствии с количеством набранных баллов (см. таблицу «Критерии оценки»).
Рекомендации по подготовке и проведению игры
Представленные в работе задания должны охватывать все основные вопросы и типы задач по изученной теме, поэтому не стоит ограничиваться 3-4 задачами, а следует существенно разнообразить их перечень, при необходимости - включить в работу теоретические вопросы, при желании — представить задания в форме тестов.
Задания со значком ∆ должны отвечать минимальному уровню программных требований; со значком О - соответствовать большинству задач учебника, они предусматривают применение знаний и умений в стандартных ситуациях. Наконец, самые трудные задания — со значком □, рассчитанные на наиболее подготовленных или интересующихся математикой ребят, требуют от последних применения знаний в более сложных ситуациях; такие задания должны носить исследовательский или творческий характер.
Задания одного уровня сложности следует расположить в порядке уменьшения важности проверяемых в них умений (наверняка найдутся ученики, которые не успеют сделать весь объем работы, а проверить основные умения необходимо).
Познакомив учащихся с правилами игры, посоветуйте им перед началом работы просмотреть все 20 заданий и выбрать оптимальный путь передвижения по Лабиринту. (В этой игре учащиеся сталкиваются с проблемой выбора, но не все с ней успешно справляются.)
Обратите внимание учеников на критерии оценки. Даже не достигнув конечной цели, можно получить хорошую оценку. Определяющую роль при ее выставлении играет не число сделанных заданий, а их сложность и качество работы.
Советы по оцениванию работы
Если задача не сделана или решена неверно, то баллы не начисляются.
При наличии ошибок или каких-либо недочетов в решении задач второго и третьего уровней сложности конечная стоимость задач может быть снижена в пределах балла в зависимости от ошибки (недочета).
Для наиболее трудных задач можно предусмотреть подсказки, использование которых снизит начальную стоимость задачи на 1 балл.
Оценки за работу объявляются и комментируются на следующем уроке.
Игрок, получивший оценку «3», несмотря на все старания, так и не дошел до сундука с сокровищами, очевидно, заблудившись в коридорах Лабиринта. Остается надеяться, что ему повезет в следующий раз и его усилия будут вознаграждены.
Оценка «4» свидетельствует о том, что игрок успешно преодолел почти все преграды на своем пути и добрался до сундука.
Игрок, получивший оценку «5», оказался более удачливым. Он не только сумел найти сокровища, но даже успел их как следует разглядеть.
Но больше всего повезло тому, кто, добравшись до сундука, унес его содержимое с собой. В результате награда — две высшие оценки.
Лабиринт
Стоимость задач
| Уровень сложности задач | Количество баллов |
| А простая О средней сложности О сложная | 1 2 3 |
Критерии оценки
| Количество баллов | Оценка |
| от 4 до 6 от 7 до 9 от 10 до 12 более 14 | 3 4 5 дополнительная 5 |
Образец карточки с заданиями


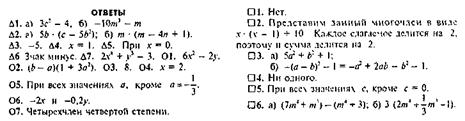
Заключение
Деятельность учащихся по усвоению содержания образования осуществляется в разнообразных формах обучения, характер которых обусловлен различными факторами: целями и задачами обучения; количеством учащихся, охваченных обучением; особенностями отдельных учебных процессов; местом и временем учебной работы учащихся; обеспеченностью учебниками и учебными пособиями и др.
Процесс обучения реализуется только через организационные формы, которые выполняют интегративную роль, обеспечивая объединение и взаимодействие всех его компонентов. Совокупность форм, объединенных по признаку связи учащихся и учителя посредством учебного материала и дополняющих друг друга, составляет организационную систему обучения.
Организационные формы и системы обучения историчны: рождаются, развиваются, заменяются одна другой в зависимости от уровня развития общества, производства, науки и образовательной теории и практики.
В моей курсовой работе рассмотрены нетрадиционные формы обучения. Это учебные экскурсии, учебные викторины, урок-практикум, урок-мастерская, дидактические игры. Их использование повышает интерес учащихся к предмету, развивает учебную деятельность школьников.
Наряду с нетрадиционными формами обучения, используются разнообразные формы учебной работы, которые носят для учащихся добровольный характер, и призваны удовлетворять их разнообразные познавательные и творческие запросы. Эти формы добровольных учебных занятий называются внеклассными. Во время внеклассных занятий можно применять нетрадиционные формы организации обучения, которые были рассмотрены в моей курсовой работе и другие.
Список используемой литературы
1. Бордовская Н. В., Реан А. А. Педагогика. Учебник для вузов. – СПб: Питир, 2001.
2. Дегтярева З.А. Математика после уроков. – Краснодар, 1996
3. Дьяченко В. К. Коллективная структура учебного процесса и ее развитие. – М., 1989.
4. Ильина Т. А. Педагогика. – М.: Просвещение, 1984.
5. Коваленко В.Г. Дидактические игры на уроках математики. – М., 1990.
6. Лихачев Б. Т. Педагогика. Курс лекций. – М.: Прометей, Юрайт, 1998.
7. Маквелов С.Г., Маквелова О.Н. Основы конструирования урока. – Армавир, 1993.
8. Махмутов М.И. Современный урок. – М. 1981.
9. Минекин Е.М. От игры к знаниям. – М., 1987.
10. Мухина С.А. Соловьева А.А. Нетрадиционные педагогические технологии в обучении. – Р.-н-Д., 2004.
11. Организационные формы обучения./ Под ред. Ю. А. Малеванного. – Киев, 1991.
12. Педагогика./ Под ред. В. А. Сластенина. – М.: Академия, 2004.
13. Педагогика./ Под ред. П. И. Пидкаситого. – М., 2002.
14. Педагогика./ Под ред. Ю. К. Бабанского. – М.: Просвещение,1998.
15. Савин Н. В. Педагогика. – М.: Просвещение, 1972.
16. Скакин М.Н. Проблемы современной дидактики. – М., 1990.
17. Сластенин В. А., Исаев И. Ф., Шиянов Е. Н. Общая педагогика. – М.: Владос, 2003.
18. Теоретико – методологические основы учебно – воспитательного процесса в школе и вузе. Сборник научных трудов. – Волгоград, 1984.
19. Харламов И. Ф. Как активизировать учение школьников. – М., 1975.
20. Харламов И. Ф. Педагогика. – Минск, 2002.
21. Чередов И. М. Система форм организации обучения в общеобразовательной школе. – М., 1987.
22. Яковлев Н. М., Сохор А. М. Методика и техника урока в школе. – М., 1985.
Похожие работы
... умственными способностями; план Трампа - вариативное, свободное, открытое учение и т.д.), многие учителя, творчески подходящие к своей профессиональной деятельности, считают главными при выборе форм организации обучения такие основания: 1) выявление детей, отличающихся характером восприятия учебной информации, типом общения со сверстниками, учителями и др.; 2)определение тех качеств, которые ...
... –ученик, многообразием видов деятельности субъектов (игровая, дискуссионно-оценочная, рефлексивная), базирующихся на активных методах обучения (проблемном, исследовательском, “методе прямого доступа”)”. [29] Глава 2. Урок как основная форма организации обучения технологии 2.1 Разработка учебно-методического комплекса организации и проведения уроков технологии Техническое творчество ...
... нецелесообразно, так как нетрадиционное может быстро стать традиционным, что в конечном счете приведет к падению у учащихся интереса к предмету. Развивающий и воспитывающий потенциал нетрадиционных форм урока можно охарактеризовать с помощью определения следующих целей обучения: - формирование у учащихся интереса и уважения к культуре страны изучаемого языка; - воспитание культуры ...
... праздника, приподнятое настроение, позволяют ребятам проявить свою инициативу, способствуют выработке у них чувства взаимопомощи, коммуникативных умений. Как правило, театрализованные уроки разделяют по форме их организации: спектакль, салон, сказка, студия и т.д. При подготовке таких уроков даже работа над сценарием и изготовление элементов костюмов становятся результатом коллективной ...
0 комментариев