Добавляйте символы или рисунки, чтобы легче было потом вспоминать

4.            Добавляйте символы или рисунки, чтобы легче было потом вспоминать.

Эффективность восстановления информации с помощью карты памяти позволяют следующие приемы.

·  Пишите разборчиво, чаще пользуйтесь заглавными и печатными буквами.

·  Важные идеи пишите более крупным шрифтом, чтобы они сразу бросались в глаза при просмотре записей.

·  Придавайте карте памяти личностный характер, внося свои специфические детали. Символ в виде часов может означать, что данный вопрос должен быть решен строго в срок. Некоторые используют стрелки для указания элементов, связанных определенными действиями или требующих таких действий.

·  Подчеркивайте слова. Используйте жирный шрифт.

·  Проявляйте творческое начало и фантазию, мозг лучше всего запоминает необычные вещи.

·  Для выделения определенных элементов и идей используйте обводящие линии самой произвольной формы.

·  При построении карты памяти располагайте лист бумаги горизонтально, это позволит увеличить рабочее пространство.

Теперь давайте устроим маленький перерыв, а потом приступим к изучению собственно математики.

<перерыв>

Стереометрия, или геометрия в пространстве,— это раздел геометрии, изучающий форму, размеры и свойства различных фигур и их положение в пространстве. Стереометрия — слово греческого происхождения (стереос — пространственный и метрео — измерять).

Стереометрия, как и планиметрия, возникла и развивалась в связи с потребностями практической деятельности человека. О зарождении геометрии в Древнем Египте около 2000 лет до н.э. древнегреческий ученый Геродот (V до н.э.) писал, что египетский фараон разделил землю, дав каждому египтянину участок по жребию, и взимал соответствующим образом налог с каждого участка. Случалось, что Нил заливал тот или иной участок, тогда пострадавший обращался к царю, а царь посылал землемеров, чтобы установить, на сколько уменьшился участок, и в соответствии с этим уменьшал налог. Так возникла геометрия в Египте, а оттуда перешла в Грецию.

При строительстве даже самых примитивных сооружений необходимо было рассчитать, сколько материала пойдет на постройку, уметь вычислить расстояния между точками в пространстве и углы между прямыми и плоскостями, знать свойства простейших геометрических фигур. Так, египетские пирамиды, сооруженные за 2—3 тысячи лет до н. э., поражают точностью своих метрических соотношений, свидетельствующих, что их строители уже знали многие стереометрические положения и расчеты.

Развитие торговли и мореплавания требовало умений ориентироваться во времени и пространстве: знать сроки смены времен года, уметь определять свое местонахождение по карте, измерять расстояние и находить направление движения. Наблюдения за Солнцем, Луной, звездами и применение законов взаимного расположения прямых и плоскостей в пространстве позволили решить многие задачи небесной механики, дали начало новой науке — астрономии.

Начиная с VII в. до н. э. в Древней Греции возникают так называемые философские школы. В них все большее значение приобретают рассуждения, с помощью которых удавалось получать новые геометрические свойства. Происходит постепенный переход от наглядно-практической к теоретической геометрии.

Одной из первых и наиболее известных таких школ была Пифагорейская (VI — V до н.э.), названная так в честь своего основателя Пифагора. Вам хорошо известно это имя (в курсе планиметрии вы изучали теорему Пифагора о соотношении длин сторон прямоугольного треугольника). Философское объяснение устройства мира пифагорейцы тесно связывали с математикой. Выделяя стихии как первоосновы бытия, древние ученые приписывали их атомам форму правильных многогранников, а именно: атомам огня — форму тетраэдра (рис. 1, а), земли — гексаэдра(рис. 1, б), воздуха — октаэдра (рис. 1, в), воды — икосаэдра(рис. 1, г). Всей вселенной присваивалась форма додекаэдра(рис. 1, д).

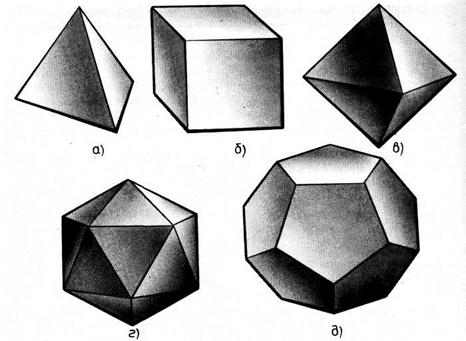
Испанский живописец Сальвадор Дали использовал этот символ в своей картине «Тайная вечеря», на которой Христос и его ученики изображены сидящими на фоне огромного прозрачного додекаэдра. Гранями додекаэдра являются правильные пятиугольники. Если стороны правильного пятиугольника продолжить до взаимного пересечения, то получится правильный звездчатый пятиугольник (рис. 2). Эта фигура, называемая также пентаграммой, была эмблемой школы Пифагора. Пентаграмме присваивалась способность защищать человека от злых духов. Вот что мы находим, читая «Фауста» Гете:

Мефистофель: Нет, трудновато выйти мне теперь, Тут кое-что мешает мне немного: Волшебный знак у вашего порога. Не пентаграмма ль этому виной?

Фауст: Но как же, бес, пробрался ты за мной? Каким путем впросак попался?

Мефистофель: Изволили ее вы плохо начертить, И промежуток в уголку остался, Там, у дверей,— и я свободно мог вскочить.

Более поздняя философская школа — Александрийская, интересна тем, что дала миру знаменитого ученого Евклида (IV до н.э.). К сожалению, жизнь его мало известна. В одном из своих сочинений математик Папп, современник Евклида, изображает его как человека исключительно честного, тихого и скромного, которому были чужды гордость и эгоизм. Насколько серьезно и строго он относился к изучению математики, можно судить по следующему известному рассказу: царь Птолемей спросил у Евклида, нельзя ли найти более короткий и менее утомительный путь к изучению геометрии, чем его «Начала». Евклид на это ответил: «В геометрии нет царского пути».

Славу Евклиду принесло его научное сочинение из 13 книг под общим названием «Начала», в котором впервые было представлено стройное аксиоматическое построение геометрии, т. е. сначала вводились основные неопределяемые понятия и постулировались их свойства (аксиомы), а все остальные утверждения (теоремы, следствия) выводились путем логических рассуждений из аксиом и ранее доказанных утверждений. На протяжении более двух тысячелетий «Начала» Евклида остаются основой изучения систематического курса геометрии.

В последние столетия возникли и развивались новые направления геометрических исследований: аналитическая геометрия, геометрия Лобачевского, проективная геометрия, топология и др. Появились новые методы, в том числе координатный и векторный, позволяющие переводить геометрические задачи на язык алгебры и наоборот. Геометрические методы широко используются в других науках: теории относительности, квантовой механике, кристаллографии и т. д.

Таким образом, мы вплотную подошли к определению многогранника. Но прежде, чем его дать, сначала давайте поговорим о геометрическом теле.

Геометрическое тело.

Точка М называется граничной точкой данной фигуры F, если среди сколь угодно близких к ней точек (включая ее саму) есть точки, как принадлежащие фигуре, так и не принадлежащие ей. Множество всех граничных точек фигуры называется ее границей. Так, например, границей шара является сфера.

Точка фигуры, не являющаяся граничной, называется внутренней точкой фигуры. Каждая внутренняя точка фигуры характеризуется тем, что все достаточно близкие к ней точки пространства также принадлежат фигуре. Так, любая точка шара, не лежащая на сфере — его границе, является внутренней точкой шара.

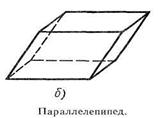
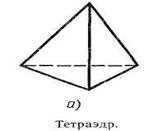
Фигура называется ограниченной, если ее можно заключить и какую-нибудь сферу. Очевидно, что шар, тетраэдр, параллелепипед — ограниченные фигуры, а прямая и плоскость — неограниченные.

Фигура называется связной, если любые две ее точки можно соединить непрерывной линией, целиком принадлежащей данной фигуре. Примерами связных фигур являются тетраэдр (см. рис. а), параллелепипед (см. рис. б), октаэдр (см. рис. 68), плоскость. Фигура, состоящая из двух параллельных плоскостей, не является связной.

Геометрическим телом (или просто телом) называют ограниченную связную фигуру в пространстве, которая содержит все свои граничные точки, причем сколь угодно близко от любой граничной точки находятся внутренние точки фигуры. Границу тела называют также его поверхностью и говорят, что поверхность ограничивает тело.

Плоскость, по обе стороны от которой имеются точки данного тела, называется секущей плоскостью. Фигура, которая образуется при пересечении тела плоскостью (т. е. общая часть тела и секущей плоскости), называется сечением тела.

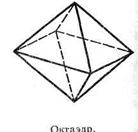
Теперь перейдем е определению многогранника. Поверхность, составленную из многоугольников и ограничивающую некоторое геометрическое тело, будем называть многогранной поверхностью или многогранником. Тетраэдр и параллелепипед — примеры многогранников. На рисунке а) изображен еще один многогранник — октаэдр. Он составлен из восьми треугольников. Тело, ограниченное многогранником, часто также называют многогранником.

Многоугольники, из которых составлен многогранник, называются его гранями. Гранями тетраэдра и октаэдра являются треугольники, гранями параллелепипеда — параллелограммы. Стороны граней называются ребрами, а концы ребер — вершинами многогранника. Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю многогранника.

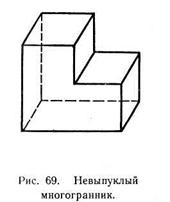
Многогранники бывают выпуклые и невыпуклые. Многогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой его грани. Тетраэдр, параллелепипед и октаэдр — выпуклые многогранники. На рисунке изображен невыпуклый многогранник, составленный из восьми многоугольников.

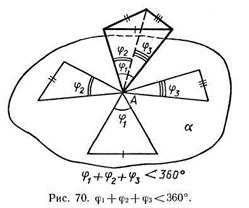
Ясно, что все грани выпуклого многогранника являются выпуклыми многоугольниками. Можно доказать, что в выпуклом многограннике сумма всех плоских углов при каждой его вершине меньше 360°. Рисунок 70 поясняет это утверждение: многогранник «разрезан» вдоль ребер и все его грани с общей вершиной А развернуты так, что оказались расположенными в одной плоскости а. Видно, что сумма всех плоских углов при вершине А, т. е..

На этом мы закончим наше сегодняшнее занятие, жду всех вас на следующем.

< Повторное проведение аутотренинга, музыка в конце сменяется на ритмичную>

Занятие 2

<аутотренинг>

Призма.

Рассмотрим два равных многоугольника и A₁A₂…A_n и B₁B₂…B_nрасположенных в параллельных плоскостях α и β так, что отрезки А₁В₁, А₂В₂, ..., А_пВ_п, соединяющие соответственные вершины многоугольников, параллельны (рис.71).

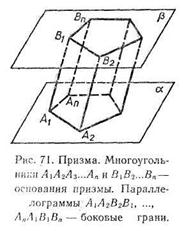Каждый из п четырехугольников A₁A₂B₂B₁, A₂A₃B₃B₂,…, A_nА₁B₁B_n является параллелограммом, так как имеет попарно параллельные противоположные стороны. Например, в четырехугольнике A₁A₂B₂B₁ стороны А₁В₁ и А₂В₂ параллельны по условию, а стороны А₁А₂ и В₁В₂ — по свойству параллельных плоскостей, пересеченных третьей плоскостью.

Многогранник, составленный из двух равных многоугольников A₁A₂...A_n и В₁В₂...В_п, расположенных в параллельных плоскостях, и п параллелограммов, называется призмой (см. рис. 71).

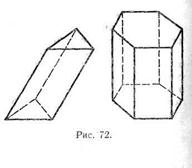
Многоугольники A₁A₂…A_n и B₁B₂…B_n называются основаниями, а параллелограммы — боковыми гранями призмы. Отрезки А₁В₁ А₂В₂, ..., А_пВ_п называются боковыми ребрами призмы. Эти ребра как противоположные стороны параллелограммов, последовательно приложенных друг к другу, равны и параллельны. Призму с основаниями A₁A₂…A_n и B₁B₂…B_n обозначают А₁А₂...A_nB₁B₂...B_n и называют п-угольной призмой. На рисунке 72 изображены треугольная и шестиугольная призмы, а на рисунке 1б — четырехугольная призма, т. е. параллелепипед.

Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы.

Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой, в противном случае — наклонной. Высота прямой призмы равна ее боковому ребру.

Прямая призма называется правильной, если ее основания — правильные многоугольники. У такой призмы все боковые грани — равные прямоугольники. На рисунке 72 изображена правильная шестиугольная призма.

Площадью полной поверхности призмы называется сумма площадей всех ее граней, а площадью боковой поверхности призмы — сумма площадей ее боковых граней. Площадь  полной поверхности выражается через площадь  боковой поверхности и площадь S_0CH основания призмы формулой:

.

Докажем теорему о площади боковой поверхности прямой призмы.

Теорема. Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы.

Доказательство. Боковые грани прямой призмы — прямоугольники, основания которых — стороны основания призмы, а высоты равны высоте h призмы. Площадь боковой поверхности призмы равна сумме площадей указанных прямоугольников, т. е. равна сумме произведений сторон основания на высоту h. Вынося множитель h за скобки, получим в скобках сумму сторон основания призмы, т. е. его периметр Р. Итак, S_6oк=Ph. Теорема доказана.

Пирамида.

Рассмотрим многоугольник A₁A₂...A_n и точку Р, не лежащую в плоскости этого многоугольника. Соединив точку Р отрезками с вершинами многоугольника, получим п треугольников (рис. 73): РА₁А₂,, РА₂А₃,, ..., РА_пА₁.

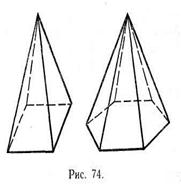
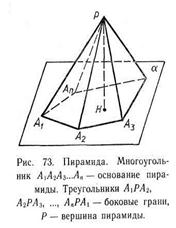Многогранник, составленный из п-угольника А₁А₂...А_п и п треугольников, называется пирамидой. Многоугольник A₁A₂...A_n называется основанием, а треугольники — боковыми гранями пирамиды. Точка Р называется вершиной пирамиды, а отрезки РА₁,, РА₂,, ..., РА_п — ее боковыми ребрами. Пирамиду с основанием A₁A₂...A_n и вершиной Р обозначают так: РA₁A₂...A_n — и называют n-угольной пирамидой. На рисунке 74 изображены четырехугольная и шестиугольная пирамиды. Ясно, что треугольная пирамида — это тетраэдр.

Перпендикуляр, проведенный из вершины пирамиды к плоскости основания, называется высотой пирамиды. На рисунке 73 отрезок РН — высота пирамиды.

Площадью полной поверхности пирамиды называется сумма площадей всех ее граней (т. е. основания и боковых граней), а площадью боковой поверхности пирамиды — сумма площадей ее боковых граней. Очевидно,

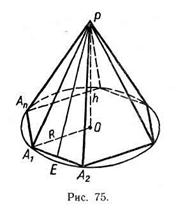Правильная пирамида. Пирамида называется правильной, если ее основание — правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой (рис. 75).

Докажем, что все боковые ребра правильной пирамиды равны, а боковые грани являются равными равнобедренными треугольниками.

Рассмотрим правильную пирамиду РА₁А₂...А_п (рис. 75). Сначала докажем, что все боковые ребра этой пирамиды равны. Любое боковое ребро представляет собой гипотенузу прямоугольного треугольника, одним катетом которого служит высота РО пирамиды, а другим — радиус описанной около основания окружности (например, боковое ребро РА₁ — гипотенуза треугольника ОРА₁ в котором OP=h, OA₁ = R). По теореме Пифагора любое боковое ребро равно , поэтому РА₁=РА₂ = ... = РА_п.

Мы доказали, что боковые ребра правильной пирамиды РА₁А₂...А_п равны друг другу, поэтому боковые грани — равнобедренные треугольники.

Основания этих треугольников также равны друг другу, так как A₁A₂...A_n — правильный многоугольник. Следовательно, боковые грани равны по третьему признаку равенства треугольников, что и требовалось доказать.

Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой. На рисунке 75 отрезок РЕ — одна из апофем. Ясно, что все апофемы правильной пирамиды равны друг другу.

Докажем теорему о площади боковой поверхности правильной пирамиды.

Теорема. Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.

Доказательство. Боковые грани правильной пирамиды — равные равнобедренные треугольники, основания которых — стороны основания пирамиды, а высоты равны апофеме. Площадь S боковой поверхности пирамиды равна сумме произведении сторон основания на половину апофемы d. Вынося множитель d за скобки, получим в скобках сумму сторон основания пирамиды, т. е. его периметр. Теорема доказана.

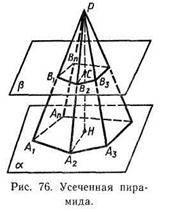Усеченная пирамида. Возьмем произвольную пирамиду РА₁А₂...А_п и проведем секущую плоскость β, параллельную плоскости α основания пирамиды и пересекающую боковые ребра в точках В₁, В₂,, .... В_п (рис. 76). Плоскость β разбивает пирамиду на два многогранника. Многогранник, гранями которого являются п-угольники А₁А₂...А_п и В₁В₂...В_п (нижнее и верхнее основания), расположенные в параллельных плоскостях, и п четырехугольников A₁A₂B₂B₁, A₂A₃B₃B₂ ,…, А_пА₁В₁В_п (боковые грани), называется усеченной пирамидой. Отрезки А₁В₁, А₂В₂, ..., А_пВ_п называются боковыми ребрами усеченной пирамиды.

Усеченную пирамиду с основаниями А₁А₂...А_п и В₁В₂...В_п обозначают так: А₁А₂...А_пВ₁В₂...В_п.

Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой усеченной пирамиды. На рисунке 76 отрезок СН — высота усеченной пирамиды.

Докажем, что боковые грани усеченной пирамиды — трапеции. Рассмотрим, например, боковую грань A₁A₂B₂B₁ (рис. 76). Стороны А₁А₂ и В₁В₂ параллельны, поскольку принадлежат прямым, по которым плоскость РА₁А₂ пересекается с параллельными плоскостями α иβ. Две другие стороны А₁В₁ и А₂В₂ этой грани не параллельны — их продолжения пересекаются в точке Р. Поэтому данная грань — трапеция. Аналогично можно доказать, что и остальные боковые грани — трапеции.

Усеченная пирамида называется правильной, если она получена сечением правильной пирамиды плоскостью, параллельной основанию. Основания правильной усеченной пирамиды — правильные многоугольники, а боковые грани — равнобедренные трапеции. Высоты этих трапеций называются апофемами.

Площадью боковой поверхности усеченной пирамиды называется сумма площадей ее боковых граней.

В качестве домашнего задания докажите следующую теорему:

Теорема. Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров оснований на апофему

Теперь давайте сделаем маленький перерыв.

<перерыв>

Прежде, чем приступить к решению задач, мы с вами рассмотрим творческие методы решения задач, которые предлагает квантовое обучение.

творческое мышление.

Как вы думаете, какими качествами обладает творческая личность?

Творческая личность наделена любопытством и интуицией, любит экспериментировать, играть, пускаться в приключения. И такой творческой личностью может стать каждый человек – и вы!

Оцените по десятибалльной шкале, насколько вы творческий человек. Стив Куртис, бизнесмен и эксперт по определению творческих задатков, всегда задает этот вопрос кандидатам на рабочее место. Место получает тот, кто ставит себе 10 баллов. Стив объясняет свой принцип так: « Все люди рождаются творческими личностями. Если человек верит в это, он всегда сможет найти оригинальные решения рутинных проблем как на работе, так и в личной жизни. И я хочу работать именно с такими людьми».

Люди определенного круга – художники, ученые и изобретатели – в нашем обществе считаются таинственными и загадочными лишь потому, что они «творческие личности». Однако у каждого из нас есть способности творчески мыслить и решать задачи. Для развития этих способностей необходимы три качества: пытливость ума, готовность рисковать и напористость в осуществлении своих планов. И найти в себе эти качества может любой человек.

Теперь давайте рассмотрим составляющие решения – мыслительные процессы:

· Вертикальное мышление - процесс пошагового движения к цели, похожий на подъем по лестнице - ступенька за ступенькой;

· Латеральное мышление – изучение проблемы под новым углом зрения, словно перепрыгивания с одной лестницы на другую;

· Критическое мышление – применение тщательного взвешивания или оценок, как при расчете осуществимости идеи или рентабельности производства какого-то либо вида продукции;

· Аналитическое мышление – расчленение проблемы или идеи на составные части, изучение по отдельности каждой части, ее связей с остальными составляющими и исследование возможности новых способов сочетания этих частей;

· Стратегическое мышление – разработка особой стратегии планирования и управления широкомасштабными операциями путем рассмотрения проекта со всех возможных точек зрения;

· Результативное мышление – энергичное решение задачи для получения желаемого результата;

· Творческое мышление – так называемый эффект «загорающейся лампочки», проявляющийся, когда имеющиеся факты комбинируются таким образом, что возникает новый взгляд на предмет. Это почти всегда связано с использованием латерального мышления.

Все эти мыслительные процессы протекают в разных частях головного мозга. В отвечающем за интуицию правом полушарии идут процессы латерального, результативного и творческого мышления, в то время как в «логическом» левом – вертикального, критического, стратегического и аналитического мышления. В действительности четкой границы категорий не существует, и многие процессы протекают одновременно в обеих половинах мозга. При решении проблем, как вообще в любой интеллектуальной деятельности, творческое и логическое мышление сочетаются. Те, кто действительно творчески подходит к любой другой ситуации, умело пользуются этой комбинацией. Важно помнить, что творчество не прекращается после вспышки озарения, а продолжается до конкретного воплощения идеи.

Процесс творческого решения проблем проходит следующие характерные стадии:

· Подготовка – Определяется проблема, цель и задача;

· Инкубация (вынашивание) – Факты «перевариваются» и систематизируются, идет брожение идей в уме;

· Озарение – идеи прорываются на поверхность сознания, как пузырьки в кипящей воде;

· Проверка – проверяется, действительно ли выработанная стратегия решает проблему;

· Применение – предпринимаются шаги по реализации найденного решения.

Теперь давайте подробнее познакомимся с тремя творческими подходами к поиску решений.

Результативное мышление

Проблемное мышление может иметь отрицательный результат. Вопросы вроде «Что же здесь не так?», «Кто все испортил?», «Почему это случилось со мной?» и т.п., концентрируют внимание на негативном, приводя к пустой трате энергии и творческих сил. Результативное мышление, напротив, дает только положительные результаты. Оно прямо противоположно проблемному мышлению и вместо топтания вокруг негатива ведет в нужном направлении. Если мышление результативное, то задаются вопросы типа «Как можно контролировать ситуацию?», «Что я могу сделать сейчас?», «Что поможет мне собраться с силами?», «В чем источник мотивации и вдохновения?», «Каким образом можно изменить ситуацию?» и т.п. При таком типа мышления проблемы, поглощающие энергию, становятся целями, дающими энергию.

Думайте не о проблеме, а о ее решении и настраивайтесь на успех. Другими словами, представляйте, как все будет происходить после претворения решения в жизнь. Это очень эффективный прием, который способен приводить к нахождению путей реализации решения. Кроме того, в этом случае создается определенное «напряжение» между проблемой и решением. Такое напряжение имеет естественную тенденцию к разрешению в положительную сторону.

Смена парадигм или «меняя лестницы».

Для того, чтобы научиться мыслить творчески, не обязательно больше работать – важно научиться думать по-другому. Зачастую при этом используется такое явление, как «смена парадигм». Парадигма представляет собой набор правил, которые используются для оценки информации и ее применения в жизни. У каждого человека есть свои парадигмы, основанные на личном опыте. Эти парадигмы очень полезны, однако иногда они играют роль ограничителя, не позволяющего принять появляющиеся возможности из-за того, что эти возможности не вписываются в рамки известного вам опыта. Жить с одной парадигмой – все равно, что постоянно смотреть в одно и то же окно, в котором виден один и тот же кусок неба, Конечно, можно прекрасно прожить жизнь, все время глядя в одно и то же окно. В конце концов, лучше иметь одно окно, чем не иметь его вообще. Прекрасный вид из окна может быть закрыт чем-нибудь полностью, и если его никогда не видеть, не будет причин думать о нем или чувствовать себя в чем-то ограниченным, не правда ли? При смене парадигм как бы приоткрывается новое окно, через которое можно увидеть разнообразные новые предметы или же старые – но под новым углом. А когда поймете, что окно не одно, сможете легко представить, что где-то может скрываться еще несколько окон. И в глубине сознания загорится огонек…, затем еще один, и еще, и еще…Благодаря смене парадигм вы можете выйти за рамки общепринятых схем мышления и найти при этом свежие решения. Однако рассуждать о смене парадигм проще, чем ее осуществлять. Хотя иногда это происходит в результате озарения, чаще всего для этого приходится топтаться вокруг проблемы, рассматривая ее со всех сторон. Чтобы выходить за рамки парадигм, важно помнить, что они существуют. Теперь давайте вернемся к метафоре с лестницей. Представьте, что вы карабкаетесь по лестнице, шаг за шагом приближаясь к решению. И вдруг узнаете, что лестница прислонена не к той стене! Иногда проблема кажется проблемой лишь потому, что ситуацию рассматривают под одним углом зрения. Если же посмотреть под другим углом, решение становится настолько очевидным, что проблема часто перестает существовать. Представьте, что вы стоите по середине комнаты, по разным углам которой к потолку привязаны веревки таким образом, что если взяться за одну из них, то до другой дотянуться невозможно. В комнате ничего нет, а у вас с собой лишь обычные предметы, которые носят в кармане или женской сумочке. Как решить эту задачу?

Большинство определяют задачу так: «Как мне дотянуться до второй веревки?» и пытаются найти способ, как продлить одну из веревок. Однако условия, заданные в задаче не позволяют этого сделать. Другими словами, «лестница приставлена не к той стене»! Если же сформулировать задачу иначе: «Каким образом я и веревка можем оказаться в одном месте?», то можно найти решение иного рода. Если привязать к концу веревки небольшой предмет и раскачать его, как маятник, то можно будет дотянуться до него, держа в руке вторую веревку. Вы заметили, как произошла смена? В следующий раз, когда перед вами встанет проблема, не забудьте посмотреть на нее со всех точек зрения и при необходимости заново сформулируйте условия задачи. Возможно для решения всего лишь понадобится изменить угол зрения.

Мозговой штурм.

Мозговой штурм – способ индивидуального и коллективного решения проблем, при котором производится запись спонтанно возникающих идей без их обсуждения. Этот метод основывается на предположении, что действительно хорошая идея появляется тогда, когда их много и есть из чего выбрать. Ситуация при этом аналогична возникающей у фотографа: для получения нескольких хороших фотографий часто приходится отснять целую пленку, на которой множество кадров обязательно окажутся плохими. Но когда делаются снимки, нельзя заранее определить, какие будут хорошими, а какие – нет. Вот почему фотограф вынужден делать много снимков.

Теперь, когда мы знаем три метода творческого мышления, будем решать задачи посредством применения этих методов. В частности, сегодня мы займемся решением задач на призму и пирамиду с использованием результативного мышления.

<Решение задач>

<Завершающий аутотренинг>

Тест для определения модальности мышления.

Люди со зрительной модальностью

·   аккуратны и дисциплинированны;

·   быстро говорят;

·   умеют организовывать работу и составлять долгосрочные планы;

·   наблюдательны (к окружающей обстановке);

·   заботятся о своем внешнем виде;

·   грамотно пишут, способны буквально мысленно «увидеть» слово;

·   лучше помнят то, что увидели, чем то, что услышали;

·   имеют проблемы с запоминанием устных указаний, пока не запишут их, и часто просят повторить;

·   много и быстро читают;

·   предпочитают читать сами, а не чтобы читали им;

·   стремятся составить общее представление и понять конечные цели и часто проявляют осторожность, пока нет полной ясности с проблемой или проектом;

·   машинально чертят или рисуют во время телефонного разговора;

·   часто отвечают на вопросы просто «да» или «нет»;

·   с большим удовольствием предложат вам демонстрацию, чем доклад;

·   изобразительное искусство любят больше, чем музыку;

·   часто знают, что сказать, но с трудом подбирают нужные слова;

·   иногда отвлекаются в ситуациях, требующих концентрации внимания;

Люди со слуховой модальностью

·   работая, разговаривают сами с собой;

·   легко отвлекаются на шумы;

·   при чтении шевелят губами и произносят слова;

·   обожают читать вслух и слушать;

·   испытывают больше проблем при письме, чем при устном изложении;

·   могут воспроизвести тембр голоса и высоту тона;

·   отличаются ритмичностью речи;

·   часто являются искусными ораторами;

·   музыку любят больше, чем изобразительное искусство;

·   обучаются, слушая, и лучше запоминают обсуждаемое, чем увиденное;

·   любят дискуссии и склонны к многословным объяснениям;

·   испытывают проблемы там, где требуется визуализация, например, при составлении цельной картины из фрагментов;

·   грамотнее произносят слова, чем пишут;

·   анекдоты предпочитают комиксам;

Люди с кинестетической модальностью

·   медленно говорят;

·   реагируют на физические поощрения;

·   привлекают внимание прикосновением;

·   разговаривая, близко подходят к собеседнику;

·   ориентируются по физическим признакам, много двигаются;

·   отличаются ранним развитием мускулатуры;

·   обучаются пробуя и действия;

·   в процессе запоминания осматривают и наблюдают;

·   при чтении водят по тексту пальцем;

·   интенсивно жестикулируют;

·   не способны долго усидеть на месте;

·   не могут запомнить географические сведения, не побывав в описываемом месте;

·   используют слова, означающие действие;

·   любят книги с «бойким» сюжетом, часто эти читатели сопровождают действия героев движениями тела;

·   могут иметь отвратительный почерк;

·   хотят все «попробовать сами»;

·   любят игры, в которых могут принять участие;

Тест для определения доминантности мышления.

а) натура с богатым воображением;

б) исследовательская натура;

в) реалистичный;

г) аналитичный;

а) организованный;

б) легко приспосабливающийся;

в) критичный;

г) любознательный;

а) спорщик;

б) люблю докапываться до сути;

в) творческий;

г) устанавливающий связи;

а) замкнутый в себе;

б) практичный;

в) академичный;

г) авантюрный;

а) точный;

б) гибкий;

в) систематичный;

г) изобретательный;

а) любящий поделиться;

б) аккуратный;

в) благоразумный;

г) независимый;

а) склонный к соревнованию;

б) педант;

в) коллективная натура;

г) логичный;

а) интеллектуальный;

б) чувствительный;

в) трудолюбивый;

г) рискованный;

а) читатель;

б) душа общества;

в) специалист по решению проблем;

г) специалист по планированию;

а) запоминание;

б) ассоциативное мышление;

в) мышление прорыва;

г) стремление докопаться до сути;

а) склонный к переменам;

б) любитель судить-рядить;

в) спонтанный;

г) нуждается в руководстве;

а) общительный;

б) ищущий;

в) осторожный;

г) склонный к рассуждениям;

а) сомневающийся;

б) проверяющий все на опыте;

в) заботливый;

г) дотошный;

а) выполняет всю работу до конца;

б) ищет благоприятные возможности;

в) генератор идей;

г) интерпретирует события;

а) работать;

б) чувствовать;

в) думать;

г) экспериментировать;

 

 

 

карточка для записи ответов:

1.      в г а б

2.      а в б г

3.      б а г в

4.      б в а г

5.      а в б г

6.      б в а г

7.      б г в а

8.      в а б г

9.      г а б в

10.    а в б г

11.    г б в а

12.    в г а б

13.    б г в а

14.    а в г б

15.    а в б г

Всего Всего Всего Всего