Навигация
Назвіть вершини, ребра та грані многогранників, зображених на малюнках
2. Назвіть вершини, ребра та грані многогранників, зображених на малюнках.
а) б)
3. Дано зображення куба АВСДА1В1С1Д1. Вкажіть:
а) точки, що не належать грані АА1ДД1;
б) точки, що належать грані ВВ1С1С.
4. Дано зображення куба АВСДА1В1С1Д1. Вкажіть:
а) пряму перетину грані АА1Д1Д і нижньої основи;
б) пряму перетину грані ВВ1С1С і нижньої основи.
5. а) Столяр за допомогою двох ниток перевіряє, чи буде стійким на рівній підлозі виготовлений стілець, що має чотири ніжки. Як для цього треба натягнути нитки? На яке теоретичне положення спирається така перевірка?
6) Щоб поверхня розпилу чотирикутної балки була плоскою, тесля робить так: позначає на ребрі балки точку А та проводить від неї у потрібному напрямі дві прямі АВ і АС у суміжних площинах поверхні балки; потім скеровує пилку по намічених прямих. Поясніть, чому у такий спосіб одержимо плоску поверхню розпилу.
6. Дано зображення куба АВСДА1В1С1Д1. Доведіть, що можна провести площину:
а) через прямі АС і СС1;
б) через прямі ВД і ДД1.
7. Зобразіть:
а) площину ![]() , яка проходить через точки А і В та не проходить через точку С;
, яка проходить через точки А і В та не проходить через точку С;
б) площини ![]() і
і ![]() , які перетинаються по прямій а.
, які перетинаються по прямій а.
8. а) Чи можуть дві площини мати тільки одну спільну точку?
б) Чи можуть три площини мати тільки одну спільну точку?
9. Користуючись малюнком, назвіть:
а) точки, що лежать у площинах АДВ і ДВС; АВС і ДСВ;
б) прямі перетину площин АВС і СДА; АВС і ДСВ.
Для класів економічного профілю
Тема. Елементи стереометрії
МЕТА
Мета теми – закласти основи для навчання учнів конструюванню геометричних тіл, дослідженню їх властивостей і вимірюванню геометричних величин, що пов’язані з ними; продовжити реалізацію ідеї моделювання реальних об’єктів і відношень між ними за допомогою найпростіших просторових геометричних фігур і відповідних математичних відношень; сприяти розвитку в учнів навичок логічного виведення, уявлень про аксіоматичний метод.
ОСНОВНІ ВИМОГИ
В результаті вивчення теми учні повинні вміти:
- встановлювати у просторі взаємне розміщення прямих і площин, зокрема паралельність і перпендикулярність прямих, прямої і площини, двох площин;
- будувати зображення фігур і на зображеннях виконувати нескладні побудови (елементів фігур, точок перетину прямої та площини, двох площин, переріз куба, тетраедра тощо);
- обчислювати відстані і кути у просторі;
- застосовувати відношення паралельності і перпендикулярності, а також вимірювання відстаней і кутів у просторі для опису об’єктів фізичного простору.
ЗМІСТ ТЕМИ
Основні поняття і аксіоми стереометрії. Паралельність прямих і площин. Паралельне проектування та його властивості. Перпендикулярність прямих і площин. Перпендикуляр і похила до площини. Перпендикулярні площини. Ортогональне проектування. Двогранні та многогранні кути.
МЕТОДИЧНІ РЕКОМЕНДАЦІЇ
Однією з головних особливостей викладання стереометрії повинно бути широке застосування геометричних образів, їх моделей і зображень. Учні повинні навчитися перш за все “бачити” розміщення прямих і площин, відповідні кути і відстані, а вже потім вміти обґрунтувати свої просторові уявлення, спираючись на означення, ознаки, властивості та інші твердження.
Після введення аксіом та наслідків з них обов’язково ознайомити учнів з технікою виконання найпростіших стереометричних креслень та побудовою перерізів. При розгляді взаємного розташування прямих у просторі доцільно довести теореми про транзитивність паралельності прямих у просторі, про рівність двох кутів із спів напрямленими сторонами, дати учням уявлення про напрям у просторі, про кути між мимобіжними прямими. Корисним буде розв’язування задач на побудову у просторі: проведення через точку прямої, паралельної до даної, прямої, що перетинає дану під заданим кутом, прямої, мимобіжної до даної, проведення через точку прямої, паралельної до даної площини і площини, паралельної даній прямій. Доцільно обговорити з учнями число розв’язків задач на побудову.
Після теореми про відрізки паралельних прямих, що містяться між двома паралельними площинами слід розглянути просторову теорему Фалеса. Що стосується відстаней у просторі, то, окрім відстаней між різними геометричними об’єктами (точки, прямі, площини, фігури, мимобіжні прямі), слід розглянути геометричні місця точок простору, пов’язані з відстанями, способи знаходження відстаней між фігурами у просторі.
Формування просторових уявлень учнів є головним завданням даної теми. Тому важливе місце треба відвести їх навчанню зображати просторові фігури на площині, а також виконувати побудови на зображеннях. Перш за все мається на увазі побудова різних елементів фігур (медіан, середніх ліній та ін.), точок перетину прямої і площини, двох площин. Крім того, достатню увагу треба звернути на побудову перерізів куба, паралелепіпеда, тетраедра. Безумовно ці тіла повинні з’явитися якомога раніше, тому що на них зручно ілюструвати усі поняття і твердження.
Конспект уроку
Тема уроку. Основні поняття стереометрії. Просторові тіла. Аксіоми стереометрії.
Мета уроку: розширити і систематизувати відомості про методи побудови курсу геометрії, про властивості основних геометричних фігур на площині та в просторі; розвивати кмітливість, творчу уяву, інтерес до геометрії.
Освоївши матеріал уроку учні повинні:
знати:
- аксіоми стереометрії та наслідки з них;
вміти:
- застосовувати аксіоми та теореми-наслідки з них до розв’язування задач.
Хід уроку
І. Вступне слово вчителя
Геометрія – одна з найдавніших наук, яка вимагає вміння логічно мислити, застосовувати теоретичні знання на практиці. До сьогоднішнього дня ви вивчили планіметрію. У цьому році ви починаєте новий розділ геометрії – стереометрію. Сьогодні ми з вами трохи пограємось на уроці. Усі знають, що найкращий спосіб вивчити що-небудь – це відкрити самому. Тому бажаю вам сьогодні якнайбільше відкриттів у знаннях та здобуття найвищих досягнень.
ІІ. Пояснення нового матеріалу
Запишіть у зошиті тему уроку. Розділ геометрії, в якому вивчають фігури у просторі, називається стереометрією. Поняття точки, прямої і площини в стереометрії первісні, не означувані. У геометрії площину уявляють необмеженою, ідеально рівною і гладенькою, що не має ніякої товщини. В планіметрії розглядають тільки одну площину. В стереометрії доводиться розрізняти багато площин.
Зображають площини у вигляді паралелограмів або кусків площини, обмежених довільними замкненими лініями. Позначають їх звичайно грецькими буквами ![]() тощо.
тощо.
У стереометрії вивчаються властивості як плоских геометричних фігур, так і неплоских. Фігура називається неплоскою (просторовою), якщо не всі її точки лежать в одній площині. Приклади неплоских фігур: куб, конус, куля.
Сформулюємо аксіоми, що виражають основні властивості точок, прямих і площин у просторі.
1. Через будь-які три точки простору, що не лежать на одній прямій, можна провести площину, і до того ж тільки одну.
2. Якщо дві різні площини мають спільну точку, то вони перетинаються по прямій, яка проходить через цю точку.
3. Якщо дві різні прямі мають спільну точку, то через них можна провести площину, і притому тільки одну.
С1 С2 С3
![]()
![]() }
}![]()
![]()
(Учні в зошитах креслять схему).
Введемо основні позначення.
| Прямі | Пряма і площина | Площини |
|
|
|
|
ІІІ. Закріплення нового матеріалу.
Гра „Лото”
Учням роздаються картки лото, на яких є відповіді на запитання. Учні називають у довільному порядку числа від 1 до 15. Біля правильної відповіді проставляється номер запитання. За кодами першого рядка створюються команди.
Запитання для карток лото
1. Розділ геометрії, що вивчає фігури у просторі, називається...
2. Якими буквами позначаються площини?
3. Основними фігурами у просторі є...
4. Знайдіть знак належності точки до прямої чи площини.
5. Знайдіть знак належності прямої до площини.
6. Задано площину. Чи існують точки, що не належать їй?
7. Скільки площин можна провести через дві різні прямі, що мають спільну точку?
8. Знайдіть знак перетину площин ![]() і
і ![]() по прямій а.
по прямій а.
9. Яка фігура є перетином двох різних площин, що мають спільну точку?
10. Знайдіть позначення мимобіжних прямих.
11. Система аксіом стереометрії складається з просторових аксіом С1-С3 та ...
12. Площину зображають у вигляді...
13. Чи можна провести площину через дві різні прямі, що мають спільну точку?
14. Вставте слово: яка б не була площина існують ..., що належать цій площині, і ..., що їй не належать.
15. Як називається фігура, яку задано так: (АВС)?
Картки лото
|
| одна |
| паралелограм | стереометрія |
| точка, пряма, площина | можна | площина | існують |
|
| аксіоми стереометрії І-ІХ | пряма, що проходить через цю точку |
| грецькі | точки |
| одна |
|
| стереометрія | паралелограм |
| аксіоми планіметрії І-ІХ | пряма, що проходить через цю точку |
| точки | грецькі |
| площина | точка, пряма, площина | існують | можна |
|
|
| можна | існують | точка, пряма, площина | площина |
| аксіоми планіметрії І-ІХ | точки | грецькі |
| пряма, що проходить через цю точку |
| одна | паралелограм |
| стереометрія |
|
| можна | існують |
| точка, пряма, площина | площина |
| одна |
| паралелограм | стереометрія |
|
| аксіоми планіметрії І-ІХ | точки | пряма, що проходить через цю точку |
| грецькі |
| точки |
| грецькі | пряма, що проходить через цю точку | аксіоми планіметрії І-ІХ |
| можна | точка, пряма, площина |
| площина | існують |
| паралелограм |
| одна |
| стереометрія |
| грецькі | точки |
| аксіоми планіметрії І-ІХ | пряма, що проходить через цю точку |
|
| одна | паралелограм | стереометрія |
|
| точка, пряма, площина | можна | існують |
| площина |
Клас поділяється на команди – дилери великого виробничого підприємства, фундатором якого є вчитель. У кожній команді призначається директор (капітан команди), розподіляються обов’язки головного бухгалтера, менеджера з реклами тощо.
– Зараз ми викликаємо директорів представництв та головних бухгалтерів на семінар-тренінг. Тут вони мають виконати завдання, які перевірять їх кваліфікацію. Найкращі повезуть до своїх філіалів великі премії (додаткові бали чи оцінки).
Одночасно для трьох капітанів пропонуються малюнки до аксіом. Завдання полягає в тому, щоб встановити, до якої аксіоми є ілюстрацією запропонований малюнок, помітити, який елемент там відсутній. Цей елемент необхідно домалювати, а потім сформулювати відповідну аксіому.
Завдання для першої команди
1) 2) 3)
Завдання для другої команди
1) 2) 3)
Завдання для третьої команди
1) 2) 3)
IV. Теоретичні завдання
Кожна команда отримує картки, на яких пропонується доведення одного з наслідків чи теоретичний матеріал про многогранники. Учні вивчають завдання, після чого один з учнів доповідає за допомогою вчителя та інших членів команди біля дошки.
– А зараз наше виробниче підприємство надасть своїм дилерам завдання провести презентацію нового продукту. Ви маєте його розглянути, а менеджери з питань реклами його представлять. Ті, хто найкраще це зробить, переможуть у грі.
Картка № 1
Теорема. Через пряму і точку, що належить даній прямій, можна провести площину, і притому тільки одну.
Дано: пряма АВ, точка С ![]() АВ.
АВ.
Довести: 1) існує ![]() {АВ, С};
{АВ, С};
2) ![]() єдина.
єдина.
Доведення
1) Проведемо пряму АС (аксіома І). АС і АВ різні, оскільки С ![]() АВ. За аксіомою С3: АВ і АС визначають площину
АВ. За аксіомою С3: АВ і АС визначають площину ![]() .
.
2) Доведемо єдиність (методом від супротивного).
Нехай існує ще одна площина ![]() , що проходить через АВ і точку С. За аксіомою С2: точки А, В і С повинні лежати на одній прямій. Це суперечить умові, що С
, що проходить через АВ і точку С. За аксіомою С2: точки А, В і С повинні лежати на одній прямій. Це суперечить умові, що С ![]() АВ. Припущення не вірне.
АВ. Припущення не вірне.
Теорему доведено.
Картка № 2
Теорема. Через три точки, що не лежать на одній прямій, можна провести площину, і притому тільки одну.
Дано: ![]() а.
а.
Довести: 1) існує ![]() ;
;
2) ![]() – єдина.
– єдина.
Доведення.
1) Проведемо прямі АВ і АС, вони різні, оскільки ![]() а. За аксіомою С3: через прямі АВ і АС можна провести площину
а. За аксіомою С3: через прямі АВ і АС можна провести площину ![]() .
.
2) Доведемо єдиність.
За теоремою 2 (якщо дві точки прямої належать площині, то вся пряма належить цій площині): ![]() . За аксіомою С3 така площина єдина.
. За аксіомою С3 така площина єдина.
Теорему доведено.
Картка № 3
Теорема. Якщо дві точки прямої належать площині, то вся пряма належить цій площині.
А ![]() |
|
![]() .
.
В ![]() |
|
Опорна задача. Якщо дві площини мають дві спільні точки, то вони перетинаються по прямій, що містить ці точки.
![]()
![]()
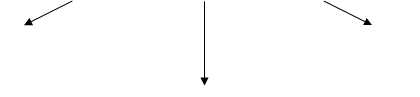 Наслідок. Пряма і площина
Наслідок. Пряма і площина
не перетинаються
(немає спільних точок) перетинаються
![]() (мають одну спільну точку)
(мають одну спільну точку)
(принаймні дві
спільні точки)
Розглянуті способи задання площини часто використовують під час побудови перерізів многогранників. Найпростішими з многогранників є куб, паралелепіпед (усі грані – паралелограми), тетраедр або трикутна піраміда (усі грані – трикутники). Якщо всі грані паралелепіпеда – прямокутники, його називають прямокутним паралелепіпедом. Якщо всі ребра тетраедра рівні, його називають правильним тетраедром.
Якщо жодна з двох точок не належить площині, а відрізок, що їх сполучає, має з цією площиною спільну точку, то говорять, що дані точки лежать по різні боки від площини. А якщо принаймні дві точки многогранника лежать по різні боки від площини, говорять, що площина перетинає многогранник. У цьому разі її називають січною площиною. Фігура, яка складається з усіх точок, спільних для многогранника і січної площини, називається перерізом многогранника даною площиною (учні демонструють моделі).
V. Висновки до уроку
Домашнє завдання.
Тестові завдання
1. а) Які з наведених фігур можуть бути тільки плоскими, а які і просторовими?
1) трикутник; 2) чотирикутник;
3) п'ятикутник; 4) шестикутник.
б) Наведіть приклади фігур, які можуть бути як плоскими, так і просторовими.
2. а) Доведіть, що вершини паралелограма АВСД лежать в одній площині.
б) Дано замкнену ламану АВСДА. Відомо, що відрізки АС і ВД перетинаються. Доведіть, що вершини ламаної лежать в одній площині.
3. а) Дано дві прямі а і в, через які не можна провести площину. Доведіть, що ці прямі не перетинаються.
б) Доведіть, що дві прямі у просторі не можуть перетинатися більше, ніж в одній точці.
4. а) Через точку проведено три прямі, які не лежать в одній площині. Скільки різних площин можна провести через ці прямі, якщо брати їх попарно?
5. б) Через точку проведено чотири прямі, кожні три з яких не лежать в одній площині. Скільки різних площин можна провести через ці прямі, якщо брати їх попарно?
6. Точки А, В, С, Д не лежать в одній площині. Доведіть, що:
а) прямі АВ і СД не перетинаються;
б) прямі АС і ВД не перетинаються.
7. а) Три площини перетинаються попарно. Скільки утвориться ліній перетину?
б) Три прямі, що не лежать в одній площині, проходять через одну точку. Через кожні дві з них проведено площину. Скільки всього проведено площин?
Для класів з поглибленим вивченням математики
Тема. Аксіоми стереометрії, найпростіші геометричні тіла.
Взаємне розташування прямих у просторі.
Взаємне розташування прямих і площин у просторі
МЕТА
Мета теми – розширити і систематизувати відомості про властивості основних геометричних фігур на площині і в просторі. Дати систематизовані знання про паралельність і перпендикулярність прямих і площин у просторі, сформувати вміння застосовувати відповідні властивості й ознаки до розв’язування задач.
ОСНОВНІ ВИМОГИ
У результаті вивчення теми учні повинні вміти:
- застосовувати аксіоми та наслідки з них до розв’язування геометричних і практичних задач;
- доводити властивості й ознаки паралельності прямих і площин та застосовувати їх до розв’язування задач;
- будувати зображення фігур і на зображеннях виконувати нескладні побудови (елементів фігур, точок перетину прямої та площини, двох площин, переріз куба, тетраедра тощо);
- обчислювати відстані і кути у просторі.
ЗМІСТ ТЕМИ
Основні поняття і аксіоми стереометрії. Техніка виконання найпростіших стереометричних креслень. Паралельні, мимобіжні прямі та прямі, що перетинаються. Напрям у просторі. Визначення кута між мимобіжними прямими.
Паралельність прямих і площин. Паралельне проектування та його властивості. Паралельність площин. Просторова теорема Фалеса.
Перпендикулярність прямих і площин. Перпендикуляр і похила до площини. Перпендикулярні площини. Ортогональне проектування. Відстані у просторі. Кут між прямою і площиною. Двогранні та многогранні кути.
МЕТОДИЧНІ РЕКОМЕНДАЦІЇ
Однією з основних цілей вивчення стереометрії є усвідомлення учнями структури логічної побудови стереометрії. Обов’язковим завданням є розвиток логічного мислення, просторової уяви, абстрактного мислення, а також ілюстрація зв’язку з реальним життям.
Курс стереометрії по відношенню до курсу планіметрії є систематизуючим і узагальнюючим. Багато тем зі стереометрії розглядається за аналогією з відповідними темами з планіметрії (вектори, координати).
У 10 класі відбувається складний процес переорієнтації в свідомості учнів: раніше всі фігури розглядалися на одній площині, тепер і сама площина стає об’єктом, самостійною фігурою і водночас носієм всіх плоских фігур з їх численними властивостями.
Однією з головних особливостей викладання стереометрії повинно бути широке застосування геометричних образів, їх моделей і зображень, залучення учнів до їх виготовлення. Учні повинні навчитися перш за все “бачити” розміщення прямих і площин, відповідні кути і відстані, а вже потім вміти обґрунтувати свої просторові уявлення, спираючись на означення, ознаки, властивості та інші твердження.
Іншим ефективним засобом формування просторових уявлень учнів є використання системи усних вправ. Вони сприяють введенню нових понять і закріпленню вже відомих. Важливе місце треба відвести навчанню зображати просторові фігури на площині, а також виконувати нескладні побудови на зображеннях. Перш за все мається на увазі побудова різних елементів фігур (медіан, середніх ліній та ін.), точок перетину прямої і площини, двох площин. Крім того, достатню увагу треба звернути на побудову перерізів куба, паралелепіпеда, тетраедра, використанню креслень і малюнків у без клітинному зошиті з використанням різних кольорів. Безумовно ці тіла повинні з’явитися якомога раніше, тому що на них зручно ілюструвати усі поняття і твердження.
Особливу увагу необхідно приділити реалізації прикладної спрямованості викладання теми. Головним в цьому є формування чітких уявлень про взаємовідношення властивостей геометричних фігур і відношень між ними і предметами навколишнього середовища.
Корисним є вироблення необхідності обґрунтовувати всі положення і розвиток інтуїції. Постійно необхідно пропонувати учням самостійно працювати на уроці і вдома, в тому числі самостійне вивчення питання з наступним виступом біля дошки.
Труднощі перших уроків стереометрії полягають в тому, що учням необхідно оперувати тільки такими геометричними фігурами, як площина, точка, пряма. Усунення цих труднощів є можливим за рахунок введення многогранників. Підсумкові уроки можна проводити як у формі конференції, так і у формі узагальнюючої лекції.
Конспект уроку
Тема уроку. Виникнення і розвиток стереометрії. Аксіоми та наслідки з них.
Мета уроку: розширити і систематизувати відомості учнів про властивості основних геометричних фігур на площині і в просторі.
Освоївши матеріал уроку учні повинні:
знати:
- аксіоми стереометрії та наслідки з них;
- аксіоматичну побудову геометрії;
вміти:
- застосовувати аксіоми та наслідки з них до розв’язування геометричних і практичних задач.
Хід уроку
І. Вступ
Логічна побудова геометрії
Кожна наука і кожний навчальний предмет у школі оперують певним колом понять, вивчають їх властивості і відношення між ними. Наприклад, фізика вивчає такі поняття, як рух, швидкість, маса, теплота, струм тощо. Граматика оперує поняттями: речення, прикметник, дієслово тощо. Геометрія – це наука про властивості геометричних фігур, і вона має справу з такими поняттями, як геометрична фігура.
– Які ви знаєте види фігур?
Наприклад, трикутник, круг, куб.
– Які відношення між фігурами вивчає геометрія?
Такі відношення між фігурами, як рівність, подібність, паралельність, перпендикулярність.
– Назвіть розглядувані перетворення фігур.
Наприклад, симетрія, поворот, подібність.
– З якими геометричними величинами має справу?
Це довжини відрізка, кола, градусна міра кута, площа, об'єм.
На відміну від інших наук геометрія має специфіку в своїй побудові. Вона побудована дедуктивно.
– Що це означає?
Дедукція (від лат. deduction – виведення) у широкому розумінні – це така форма мислення, коли нова думка виводиться суто логічно з деяких даних думок-посилань. У вужчому розумінні дедукція – це такий умовивід, внаслідок якого одержуються нові знання про предмети або групи предметів на основі вже наявних знань про досліджувані предмети.
– Що вивчає планіметрія? Які її найпростіші фігури?
У планіметрії вивчаються фігури на площині. Найпростішими фігурами в планіметрії є точка і пряма.
Ці два поняття належать до первісних понять, яким умовились не давати означень і використовувати їх при означенні інших понять. Наприклад, серединним перпендикуляром до відрізка називається пряма, яка перпендикулярна до цього відрізка і проходить через його середину. Тут серединний перпендикуляр означається через первісне поняття «пряма».
Потреба в первісних поняттях і їх роль в геометрії саме і пов'язані з дедуктивним характером її побудови. Справді, в геометрії кожне нове поняття, крім первісних, означається або на основі первісних, або на основі раніше означених понять. Розглянемо ще один приклад.
– Що називають квадратом?
Як відомо, квадратом називають прямокутник, у якого всі сторони рівні.
– Через яку фігуру означається прямокутник?
Прямокутник означається через паралелограм, у якого всі кути прямі.
– Дайте означення паралелограма.
Паралелограм означається через чотирикутник.
Маємо ланцюжок понять, який не може бути нескінченним. Тому виникає потреба невелику кількість понять прийняти без означення (первісні поняття), а через них означати інші.
![]()
![]() квадрат
квадрат
![]()
![]() прямокутник
прямокутник
![]()
![]() паралелограм
паралелограм
![]()
![]() первісні поняття
первісні поняття
Крім точки і прямої, первісними поняттями планіметрії є поняття „належати” для точок і прямих, „лежати між” – для трьох точок прямої, „довжина відрізка”, „градусна міра кута”. Первісні поняття, як і більшість означуваних, походять від об'єктів, що існують реально, і є абстракцією від них. Наприклад, поняття „площина” походить від реальної поверхні кришки стола або поверхні озера. Однак площину ми уявляємо необмежене продовженою, вона не має товщини.
– Від якого реального об’єкта абстрагують пряму?
Пряма образ туго натягнутої нитки або дроту. Проте пряма в геометрії не має кінців і уявляється необмежене продовженою, вона не має товщини.
Крім первісних і означуваних понять геометрія оперує твердженнями, що виражають властивості понять. Вони бувають двох видів: аксіоми і теореми. Твердження, що виражають властивості найпростіших фігур (первісних понять) і приймаються без доведення, називаються аксіомами. Твердження, що виражають властивості геометричних фігур і доводяться, мають назву теорем. Потреба і роль аксіом теж спричинені дедуктивним характером побудови геометрії. Тут ми маємо аналогічну схему, бо кожне нове твердження доводиться на основі раніше відомого, вже доведеного твердження і т. д. Оскільки ланцюжок тверджень не може бути нескінченним, виникає потреба невелику їх кількість умовитись прийняти без доведення і використовувати при доведенні інших.
– Пригадаємо аксіоми планіметрії, скориставшись для цього таблицею.
– Проаналізуємо означення „Суміжні кути” з погляду того, через які раніше відомі поняття воно формулюється. Пригадаємо його.
Два кути називаються суміжними, якщо одна їх сторона спільна, а інші сторони цих кутів є додатковими півпрямими.
– Через які поняття воно означається?
Воно означається через поняття сторона кута та півпряма.
– Виділимо основні поняття, відношення та величини.
Основні поняття: точка і пряма, основні відношення: лежати між, лежати на, основні величини: градусна міра кута.
– Як висновок, розглянемо наступну схему побудови геометрії.
1. Перелічуються первісні (неозначувані) поняття.
2. Формулюються аксіоми про властивості первісних понять.
3. За допомогою первісних та раніше означених понять формулюються означення нових понять.
4. На основі аксіом, доведених раніше тверджень і означень доводяться нові твердження.
ІІ. Вивчення аксіом стереометрії та наслідків з них.
Стереометрія – це розділ геометрії, що вивчає фігури у просторі. Найпростішими фігурами простору є:
- точка: А, В, С,...
- пряма: а, в, с,...
- площина: ![]() ,..., (АВС).
,..., (АВС).
Термін „стереометрія” походить від гр. ![]() – об'ємний, просторовий і
– об'ємний, просторовий і ![]() – вимірюю. Оскільки площина – нова найпростіша фігура, то треба сформулювати аксіоми, що виражають властивості площини. Розглянемо три аксіоми стереометрії, зведені в одну таблицю.
– вимірюю. Оскільки площина – нова найпростіша фігура, то треба сформулювати аксіоми, що виражають властивості площини. Розглянемо три аксіоми стереометрії, зведені в одну таблицю.
Оскільки точка і пряма також є основними фігурами простору, то всі аксіоми планіметрії переходять у стереометрію і система аксіом стереометрії складається з дев'яти аксіом планіметрії і трьох аксіом групи С.
У планіметрії ми мали одну площину, на якій розташовувались всі розглядувані нами фігури. У стереометрії нескінченно багато площин. У зв’язку з цим формулювання деяких аксіом планіметрії в якості аксіом стереометрії вимагають уточнення. Це стосується аксіом IV, VII, VIII, IX.
IV. Пряма, що належить площині, розбиває цю площину на дві півплощини.
VII. Від півпрямої на площині, що її містить, у задану півплощину можна відкласти кут з заданою градусною мірою, меншою 180○, і лише один.
VIII. Який би не був трикутник, існує рівний йому трикутник у даній площині у заданому розташуванні відносно даної півпрямої у цій площині.
ІХ. На площині через дану точку, що не лежить на даній прямій, можна провести не більше однієї прямої, паралельної даній.
Наслідки з аксіом
Теорема 1. Через пряму і точку, що належить даній прямій, можна провести площину, і притому тільки одну.
Дано: пряма а, точка В ![]() а.
а.
Довести: 1) існує ![]() {а, В};
{а, В};
2) ![]() єдина.
єдина.
Доведення
1) Виберемо на прямій а довільну точку А. Проведемо пряму в ![]() {А;В} (аксіома І). а і в різні, оскільки В
{А;В} (аксіома І). а і в різні, оскільки В ![]() а. За аксіомою С3: а і в визначають площину
а. За аксіомою С3: а і в визначають площину ![]() .
.
У ході доведення вчитель разом з учнями шляхом системи запитань складає таблицю.
– Яка аксіома стереометрії обґрунтовує можливість проведення площини?
– На яку додаткову побудову наштовхує нас ця аксіома?
– Яка аксіома обґрунтовує можливість проведення прямої?
– Через які точки проведемо ще одну пряму?
– Яка аксіома обґрунтовує можливість вибору точки А?
| Твердження | Обґрунтування |
| 1. Виберемо на прямій а довільну точку А 2. Через А і В можна провести пряму в 3. Прямі а і в різні 4. Через прямі а і в можна провести площину 5. Площина через пряму а і точку В | 1. За аксіомою про існування точок, які належать прямій 2. За аксіомою про можливість проведення прямої через дві точки 3. Оскільки точка В не належить прямій а 4. За аксіомою про можливість проведення площини через дві прямі, які мають спільну точку 5. Тому що |
2) Доведемо єдиність (методом від супротивного).
Нехай існує ще одна площина ![]() , що проходить через а і точкуВ. За аксіомою С2: точка В належить прямій а. Це суперечить умові, що В
, що проходить через а і точкуВ. За аксіомою С2: точка В належить прямій а. Це суперечить умові, що В ![]() а. Припущення не вірне.
а. Припущення не вірне.
Теорему доведено.
Теорема 2. Якщо дві точки прямої належать площині, то вся пряма належить цій площині.
А ![]() |
|
![]() .
.
В ![]() |
|
 Наслідок. Пряма і площина
Наслідок. Пряма і площина
не перетинаються
(немає спільних точок) перетинаються
![]() (мають одну спільну точку)
(мають одну спільну точку)
(принаймні дві
спільні точки)
(Цю теорему учні доводять зі складанням таблиці і оформлюють вдома самостійно).
Теорема 3. Через три точки, що не лежать на одній прямій, можна провести площину, і притому тільки одну.
Дано: ![]() а.
а.
Довести: 1) існує ![]() ;
;
2) ![]() – єдина.
– єдина.
Учитель разом з учнями складає таблицю – колективний пошук доведення, оформлюють доведення учні вдома самостійно.
| Твердження | Обґрунтування |
| 1. Проведемо прямі АВ і АС 2. Прямі АВ і АС різні 3. Через прямі АВ і АС можна провести площину 4. Точки А, В, С належать площині | 1. За аксіомою про можливість проведення прямої через дві точки 2. Точки А, В і С не лежать на одній прямій 3. За аксіомою про можливість проведення площини через дві прямі, які мають спільну точку 4. Точки А, В і С належать до прямих АВ і АС, а вони належать площині за побудовою |
Доведення.
1) Проведемо прямі АВ і АС, вони різні, оскільки ![]() а. За аксіомою С3: через прямі АВ і АС можна провести площину
а. За аксіомою С3: через прямі АВ і АС можна провести площину ![]() .
.
2) Доведемо єдиність.
За теоремою 2 (якщо дві точки прямої належать площині, то вся пряма належить цій площині): ![]() . За аксіомою С3 така площина єдина.
. За аксіомою С3 така площина єдина.
Теорему доведено.
ІІІ. Задачі на доведення
Задача 1. Точки А, В, С і Д не лежать в одній площині. Доведіть, що прямі АВ і СД не перетинаються.
Доведення.
– Скористаємось методом від супротивного.
– Яке можемо зробити припущення?
– Маємо дві прямі, що перетинаються. Яке з щойно вивчених тверджень можемо застосувати?
– Якщо прямі АВ і СД визначають площину ![]() , то який висновок можемо зробити щодо точок?
, то який висновок можемо зробити щодо точок?
– У чому полягає отримане протиріччя?
Нехай прямі АВ і СД перетинаються, тоді за аксіомою С3: ![]() , а це означає, що точки А, В, С і Д лежать в одній площині. Отримали протиріччя з умовою задачі. Значить прямі АВ і СД не перетинаються.
, а це означає, що точки А, В, С і Д лежать в одній площині. Отримали протиріччя з умовою задачі. Значить прямі АВ і СД не перетинаються.
Задача 2. Чотири точки не лежать в одній площині. Чи можуть будь-які три з них лежати на одній прямій.
Доведення.
– Яке можна висунути припущення?
– Яке відоме вам твердження можна застосувати?
– З якою умовою ми отримали протиріччя?
Нехай три точки лежать на одній прямій, а четверта не належить цій прямій. Тоді за теоремою-наслідком 1 можна провести єдину площину, якій належить дані пряма і точка. Це означає, що задані умовою чотири точки належать одній площині. За умовою задачі це не можливо. Значить будь-які три з цих точок не можуть лежати на одній прямій.
IV. Підсумок уроку
Сьогоднішній урок ми присвятили ідеї дедуктивної побудови геометрії, походженню та ролі первісних понять і аксіом, пригадали аксіоми планіметрії, ознайомилися з аксіомами стереометрії та наслідками з них. Завершити урок хочеться прикладами використання аксіом та їх наслідків у виробничій діяльності людини.
1) Тесляр перевіряє, чи розміщуються кінці ніжок стола в одній площині, від чого залежить стійкість стола. Він натягує нитки на кінці ніжок і перевіряє, чи перетинаються вони (аксіома С3).
2) Тесляр перевіряє якість поверхні стола, що виготовляється, прикладаючи до кришки в різних напрямках лінійку. Якщо між лінійкою і кришкою стола немає просвітів, то стіл виготовлено якісно (теорема 2).
3) На теоремі 3 ґрунтується будова штативів для фотоапаратів і різних геодезичних приладів. Кінці ніжок штативів належать одній площині, внаслідок чого прилад займає стійке положення.
Тестові завдання
2. На малюнку зображено куб АВСДА1В1С1Д1. Знайдіть кути трикутника В1Д1С.
3. Як розмістити три прямі так, щоб вони утворили 12 прямих кутів?
4. Чи вірно, що пряма, яка має з колом тільки одну спільну точку, є дотичною до кола в цій точці:
1) на площині; 2) у просторі?
4. Довести, що через дві довільні точки можна провести хоча б одну площину.
5. Чи можна стверджувати, що всі точки кола належать площині, якщо це коло має з даною площиною:
1) дві спільні точки; 2) три спільні точки.
6. Через три точки можна провести дві різні площини. Як розташовані ці точки?
Додаток В
СУМСЬКИЙ ДЕРЖАВНИЙ ПЕДАГОГІЧНИЙ УНІВЕРСИТЕТ ІМ. А. С. МАКАРЕНКА
СТВОРЕННЯ І АПРОБАЦІЯ
МЕТОДИЧНОГО КОМПЛЕКСУ ДЛЯ ВЧИТЕЛІВ
МАТЕМАТИКИ
У ПРОФІЛЬНИХ ГРУПАХ УЧНІВ
Автор проекту: студентка
СДПУ ім. А. С. Макаренка
V курсу
фізико-математичного факультету
Шишенко І. В.
СУМИ 2004
Мета проекту
1. Створення методичного комплексу для роботи вчителів математики з профільними групами учнів, а саме: навчальні посібники, дидактичні та діагностичні матеріали, технології, проекти, дослідницькі праці, методичні розробки.
2. Апробація комплексу шляхом створення такої системи навчання на експериментальному майданчику, що дозволить реалізувати основні принципи профільного навчання математики.
3. Задачами проекту є розробка системи уроків, методичних і навчальних посібників, після чого – організувати вивчення математики за чотирма напрямками: загальнокультурним, природничим, економічним та фізико-математичним. Кожен учень має обрати свій напрямок вивчення математики і разом з педагогами впродовж двох років (10-11 класи) реалізувати освітню програму, створену на базі попередньо розробленого методичного комплексу.
Завдання проекту
1. Створення творчої команди для написання методичних розробок.
2. Дослідження анналів світової профільної освіти.
3. Створення методичного комплексу для викладання математики у профільних групах учнів.
4. Розробка системи моніторингу і оперативної оцінки експерименту.
5. Укладення договору з міським управлінням освіти Сумської обласної Ради про відкриття експериментальних майданчиків..
6. Проведення педагогічного експерименту (апробація створеного методичного комплексу).
7. Підведення підсумків експерименту.
8. Корегування та розвиток методичних розробок.
9. Видання та розповсюдження розробок методичного комплексу.
10. Оцінка ефективності проекту.
Обґрунтування необхідності проекту
Система загальної середньої освіти України сьогодні на порозі нових суттєвих змін – впровадження профільності навчання у старшій школі. Перехід до профільного навчання розпочнеться у 2007 році, але у 2004 н.р. розпочався підготовчий період переходу до профільної старшої школи. Багато загальноосвітніх закладів впроваджують і випробовують різні механізми здійснення профільного навчання. Але аналіз сучасної педагогічної літератури показує, що однією з головних проблем при організації ефективного профільного навчання залишається брак його навчально-методичного забезпечення: література, періодика, навчально-наочні посібники, програмні продукти, педагогічні технології, методичні розробки.
У зв’язку з введенням профільного навчання на старшому ступені школи більша частина підручників, методичних та дидактичних розробок підлягає оновленню чи повній переробці. Також кожний новостворений методичний засіб, підручник, окрім отримання експертної оцінки, має пройти експериментальну перевірку в масових школах на відповідність їх змісту основним принципам дидактики.
Усунення вказаних проблем і недоліків ми передбачаємо через реалізацію відповідного проекту.
Новизна
Використовуючи можливості профільного навчання, буде здійснена спроба розробити та реалізувати методичний комплекс для роботи з профільними групами учнів.
У ході інформаційного дослідження не вдалося виявити відповідні розробки методичних систем забезпечення профільного навчання в Україні.
Новизна проекту полягає в тому, що він дає можливість забезпечити компетентний підхід до розв’язання однієї з найбільш значущих проблем, пов’язаних з організацією профільного навчання старшокласників, – проблеми забезпечення учнів і вчителів якісною літературою.
Даний курс передбачає, що з учнями працюватимуть два вчителя одночасно, передусім використовуючи діалогічні методи навчання. Це надасть можливість кожній дитині отримати компетентні відповіді на всі запитання. З іншого боку, два вчителя зможуть забезпечити інтенсивність навчання, про що свідчить досвід тренінгів "Нова Доба". Крім того, з невеликими групами учнів передбачається проведення додаткових занять, а в якості наукових керівників дослідницької роботи учнів залучатимуться викладачі вищих навчальних закладів.
Цільова аудиторія
· вчителі математики;
· учні 10-11 класів загальноосвітніх та профільних навчальних закладів;
· адміністратори освіти.
Життєздатність
Проект може мати реальне продовження, а саме:
· розробка та опис програмного забезпечення уроків математики у профільній школі;
· започаткування періодичного видання, що має забезпечити потреби профільної освіти математики;
· подальші розробки аналогічних методичних комплексів для інших наук.
Показники успіху
Проект можна вважати успішно реалізованим за умови:
1) позитивних відгуків та рецензій спеціалістів на методичний комплекс для викладання математики у профільних групах учнів;
2) підвищення зацікавленості та досягнень учнів, що беруть участь у проекті, при вивченні математики, що визначать тести, контрольні роботи тощо;
3) видання та розповсюдження розробок методичного комплексу;
4) дотримання строків та бюджету проекту.
Термін виконання проекту - 36 місяців.
План дій
У перший рік реалізації проекту планується створити творчу команду, дослідити аналоги світової практики у сфері профілювання освіти, створити методичний комплекс і необхідні додатки до нього, отримати дозвіл відповідних структур для відкриття експериментальних майданчиків у школах міста.
На другому та третьому роках проекту планується апробувати створені розробки в ході педагогічного експерименту, скорегувати і вдосконалити їх за результатами підсумків експерименту. Завершити проект планується оцінкою його ефективності.
Ассессмент
Кількісну оцінку ефективності проекту можна провести наступними методами:
· психологічне тестування учнів для оцінки мікроклімату колективу, самопочуття дитини;
· проведення контрольних робіт для оцінки якості набутих учнями знань, умінь і навиків;
· анкетування учасників проекту на предмет доцільності розробки методичного комплексу;
· бесіди з учнями та вчителями експериментальних майданчиків;
· спостереження за роботою контрольних та експериментальних класів;
· психолого-педагогічна характеристика учнів;
· кількісний та якісний аналіз експериментальних даних, отриманих у ході апробації;
· відгуки та рецензії спеціалістів на роботу творчої команди проекту.
Прогнозовані результати проекту
1. Створення творчої команди із 7 спеціалістів для написання і апробації методичного комплексу для викладання математики у профільних групах учнів.
2. Створення вищезазначеного комплексу для учнів 10-11 класів.
3. Позитивна динаміка у досягненнях з математики більшості учнів, що беруть участь у проекті.
4. Система діагностики результатів експерименту.
5. Система психологічних тестів для оцінки мікроклімату колективу, самопочуття дитини (по 2 методики на кожну категорію);
6. Комплексні завдання для оцінки якості набутих учнями знань, умінь і навиків (для кожної теми).
7. Презентаційні матеріали методичного комплексу для адміністраторів освіти.
8. Дозвіл міського управління освіти Сумської обласної Ради для відкриття 2-х експериментальних майданчиків на базі шкіл міста (2 експериментальних і 2 контрольних класів, приблизно 120 учнів).
9. Експериментальні дані, отримані у ході апробації, аналіз цих даних, а також пропозиції щодо вдосконалення розробленого методичного комплексу.
10. Видання та розповсюдження розробок методичного комплексу.
11. Додатковий досвід роботи вчителів з інноваційними педагогічними розробками.
Очікуваний зовнішній ефект
1. Досягнення всіма учнями обов’язкових результатів навчання, а для деяких груп учнів – оволодіння методологічними знаннями, загально навчальними вміннями і загальнонауковими методами пізнання, що дозволять розв’язувати задачі творчого характеру, вести дослідницьку роботу.
2. Підвищення зацікавленості у вивченні предметів.
3. Покращення мікроклімату в колективі.
4. Впровадження методичних розробок у школах України.
5. Формування у учнів уявлень про майбутній профіль діяльності.
Оцінка ресурсів
Людські ресурси
| необхідні | доступні |
| менеджер | менеджер |
| вчитель математики (спеціаліст) | вчитель математики (спеціаліст) |
| вчитель математики (спеціаліст) | вчитель математики (спеціаліст) |
| вчитель математики (методист, ВК) | - |
| вчитель математики (методист, ВК) | - |
| науковий керівник | - |
| психолог | - |
Матеріальні ресурси
| необхідні | доступні |
| приміщення | приміщення |
| література | література |
| видаткові матеріали | - |
| комп'ютер | комп'ютер |
| принтер | принтер |
| програмне забезпечення | програмне забезпечення |
| обладнання для проведення уроків | обладнання для проведення уроків |
Грошові ресурси
| необхідні | доступні |
| прямі | - |
| оплата праці задіяним спеціалістам | - |
| сплата податків | - |
| придбання видаткових матеріалів | - |
| видання методичних розробок | - |
| непрямі | |
| оренда обладнання | - |
| подорожі (відрядження) | - |
| оплата Інтернету | - |
| оплата послуг бібліотеки | - |
Аналіз проекту
| Сильні сторони · відсутність вітчизняних аналогів до розробки методичного комплексу – актуальність розробки; · напрацьована теорія профілювання освіти; · наявність певного педагогічного досвіду; · підтримка проекту з боку досвідчених колег, в тому числі і з боку адміністраторів освіти; · стартовий пакет знань щодо технології проектування; · розвинуті контакти з молодими талановитими педагогами. | Слабкі сторони · відсутність вітчизняних аналогів до розробки методичного комплексу – недостатньо напрацьована теоретична база; · відсутність власного досвіду у написанні і управлінні проектами; · відсутність команди; · відсутність експериментальних майданчиків. |
| Можливості · можливості подальшої співпраці команди; · можливість використання отриманого досвіду у подальшій роботі; · можливість продовження проекту у подальших розробках; · можливість впровадження методичного комплексу в школах України; · можливість розвитку основ профільної освіти. | Небезпеки · відсутність необхідних спеціалістів і (або) недостатній рівень залучених спеціалістів; · неузгодженість у команді; · неадекватність бюджету. |
| БЮДЖЕТ ПРОЕКТУ | |
| СТАТТІ ЗАТРАТ | СУМА ВИТРАТ |
| Заробітна плата: | |
| менеджер | 6 963.52 |
| вчитель математики (методист, ВК) | 13 653.81 |
| вчитель математики (методист, ВК) | 13 653.81 |
| вчитель математики (спеціаліст) | 10 302.55 |
| вчитель математики (спеціаліст) | 10 302.55 |
| науковий керівник | 12 923.15 |
| психолог | 4 744.02 |
| ергономіст | 3 235.92 |
| Поїздки: | |
| до м. Київ | |
| проїзд | 280 |
| добові | 72 |
| по м. Суми | 120 |
| Видаткові матеріали: | |
| канцелярські товари | 200 |
| оренда Інтернету | 400 |
| обслуговування бібліотеки | 200 |
| Загальна сума
| 77 051.33 |
| Інші витрати
| 15 410.27 |
| Всього
| 92 461.6 |
[1] Жозеф Марі де Местр (1753-1821) – граф, французький публіцист, філософ, релігійний та політичний діяч.
Похожие работы
... може бути компетентною або некомпетентною в певних питаннях, тобто мати компетентність (компетентності) у певній галузі діяльності. Саме тому, одним із результатів навчання курсу «Застосування ІКТ у навчальному процесі з математики» вбачається формування в майбутніх вчителів відповідних ключових фахових компетентностей. Зазначене вище наштовхнуло на дослідження компетентностей: внаслідок чого ...
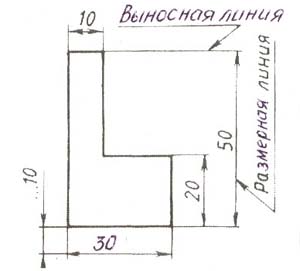
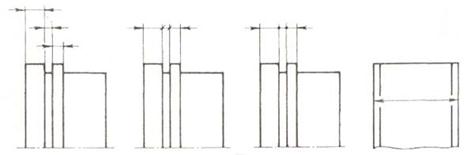
... засвоєні. До такого відпрацьовування можуть підключатися й учні першої групи як консультанти, помічники учителя. Розділ 2. Методика проведення уроків з виконання диференціального підходу на прикладі теми: „Нанесення розмірів” 2.1 Нанесення розмірів на кресленнях Питання, пов'язані із забезпеченням креслення необхідними розмірами, продумуються у процесі визначення кількості та змісту ...
... і відношення в класі виникають на основі другорядних, часто педагогічне небезпечних форм спілкування. Отже оптимальна організація педагогічного спілкування в навчальному процесі - актуальна проблема сучасної школи. За визначенням О.О. Леонтьєва "... оптимальне педагогічне спілкування - це таке спілкування вчителя із школярами в процесі навчання, яке створює найкращі умови для розвитку мотивації ...
... у фінансовій сфері. Таке означення показує, що ці задачі можуть використовуватися протягом всього учбового процесу. Останнім часом посилився пошук шляхів активізації пізнавальної діяльності учнів у процесі навчання математики за допомогою задач. Введення математичних задач фінансового змісту в шкільний курс ґрунтується на засадах та принципах процесу активізації пізнавальної діяльності учнів. ...



0 комментариев