Навигация
Реализация общедидактических принципов в организации занятий в ДОО
1.3 Реализация общедидактических принципов в организации занятий в ДОО
В дошкольном возрасте закладываются основы знаний, необходимых ребенку в школе. Математика представляет собой сложную науку, которая может вызвать определенные трудности во время школьного обучения. К тому же далеко не все дети имеют склонности и обладают математическим складом ума, поэтому такое важное значение имеет оптимальная организация занятий при математической подготовке детей к школе.
И родители, и педагоги знают, что математика – это мощный фактор интеллектуального развития ребенка, формирования его познавательных и творческих способностей. Самое главное – это привить ребенку интерес к познанию. Для этого занятия должны строиться с учетом всех общедидактических принципов, проходить в увлекательной игровой форме.
Постепенно у детей пробуждается интерес и к самому предмету обучения.
Обучение математике, как и любому учебному предмету, может стать эффективным средством формирования личности, достичь непосредственной цели – прочного и сознательного усвоения ее содержания – лишь в случае, если в основу обучения будут положены определенные положения, вытекающие из основных закономерностей дидактики, подтвержденные опытом обучения. [13]
Система таких положений, специально ориентированная на особенности математики как учебного предмета, и составляет основное содержание общедидактических принципов, применяемых в организации занятий по РЭМП. Наиболее важные принципы, характеризующие подход к обучению основам математики в детском саду, – принцип наглядности, принцип воспитывающего обучения, принцип научности, принцип сознательности и активности обучения, принцип систематичности и последовательности и др. Владение этими принципами необходимо педагогу для того, чтобы правильно организовать свой труд, грамотно, квалифицированно анализировать различные учебные пособия и методические разработки, которыми ему придется пользоваться в своей работе. [8]
А.А. Столяр предлагает систему общедидактических принципов дополнить двумя принципами, характерными для обучения математике:
1) курс математики должен отражать фундаментальные идеи и логику современной математики (в соответствии с уровнем мыслительной деятельности дошкольников на разных возрастных этапах);
2) процесс обучения математике должен строиться подобно процессу исследования в математике, то есть, он должен имитировать процесс творческого поиска в математике (в определенной мере, в какой это допускает уровень мыслительной деятельности детей дошкольного возраста).
Первый принцип относится к построению содержания обучения математике и в определенной степени конкретизирует дидактический принцип научности.
Второй принцип относится к построению процесса обучения и конкретизирует дидактический принцип развивающего обучения. [14]
В методической литературе по математическому развитию общепризнанной является следующая система дидактических принципов:
1. Принцип воспитания в развитии математических представлений.
2. Принцип научности в обучении математике.
3. Принцип сознательности, активности и самостоятельности в развитии математических представлений.
4. Принцип систематичности и последовательности в развитии математических представлений.
5. Принцип доступности в развитии математических представлений.
6. Принцип наглядности в развитии математических представлений.
7. Принцип индивидуального подхода к учащимся в развитии математических представлений.
Принцип воспитания
Общей целью воспитания в детском саду является подготовка к всестороннему развитию личности, способной построить и защитить общество. Всестороннее развитие личности предполагает умственное и нравственное развитие, богатую духовную жизнь, физическое и эстетическое развитие. Реализация общей цели воспитания требует поэтому решения более частных задач, которые рассматриваются в качестве составных частей или сторон воспитания: трудовое, нравственное, умственное, эстетическое и физическое воспитание. Выделение составных частей воспитания опирается на объективные требования общества в развитии определенных свойств (качеств) личности. [5]
Но воспитание в процессе обучения вообще и математике в частности как принцип обучения имеет и свою содержательную направленность, которая определяется формированием мировоззрения и морали. Чтобы каждый ребенок мог действовать в соответствии с принципами мировоззрения и морали, он должен сформировать у себя такие черты характера, как трудолюбие, сила воли, скромность, честность по отношению к самому себе и другим людям.
Мировоззрение, базирующееся на научном знании и практическом жизненном опыте, связывает в единое целое эти свойства личности. Отсюда вытекают возможность и необходимость передачи всем людям знаний о закономерностях развития природы, общества и человеческого мышления, чтобы они могли сознательно осуществлять практическую деятельность. [9]
Следовательно, в формировании убеждений возрастает роль процесса усвоения знаний. В связи с этим в развитии математических представлений (как и каждого раздела образовательной программы) необходимо повышать активность детей и возбуждать у них интерес к вопросам, имеющим мировоззренческое значение. Важную роль в этом приобретает освещение в преподавании математики новых идей современной науки.
При планировании содержания, средств, методов и форм обучения педагог призван обеспечить решение всего комплекса образовательных, воспитательных и развивающих задач. [5]
Принцип научности
Требование научности содержания образования было выдвинуто в советской педагогической литературе еще в работах Н. К. Крупской.
Статус дидактического принципа требование научности в обучении приобрело с 1950г., когда оно было сформулировано и обосновано М. Н. Скаткиным. В дальнейшем Л.Я. Зорина показала, что под научностью содержания образования следует понимать такую его качественную характеристику, которая удовлетворяет трем признакам:
а) соответствие содержания образования уровню современной науки;
б) создание верных представлений об общих методах научного познания;
в) показ важнейших закономерностей процесса познания. [12]
Эти условия взаимосвязаны между собой, ибо реализация каждого из последующих обусловлена выполнением предыдущих; каждое предыдущее условие является необходимой базой для реализации последующего.
В организации занятий по развитию математических представлений дошкольников у педагогов имеется много возможностей показать закономерности процесса познания. Именно поэтому в процессе обучения основам математике шире должны внедряться проблемное обучение и разнообразные исследовательские приемы.
В процессе реализации принципа научности воспитатель должен соблюдать также принцип доступности, чтобы содержание, формы и методы обучения учитывали реальные возможности воспитанников. При этом необходимо учитывать и то, что принцип доступности предполагает обучение на достаточно высоком уровне трудности. Однако это можно достигнуть лишь при наилучшем сочетании индивидуальных и коллективных форм познавательной деятельности дошкольников в обучении.
Принцип систематичности и последовательности
Нельзя овладеть наукой, не изучая ее в определенной системе. В такой же мере нельзя успешно развивать познавательные и творческие способности дошкольников без строго продуманной системы их обучения и воспитания.
Систематичность в развитии математических представлений предполагает соблюдение определенной последовательности в изучении учебного материала и постепенное овладение основными понятиями дошкольного курса математики.
Последовательность в обучении математике означает, что обучение осуществляется в соответствии с правилами обучения: а) от простого к сложному; б) от легкого к трудному; в) от известного к неизвестному;
г) от представлений к понятиям; д) от знания к умению, от него к навыку. [7]
Принцип доступности
Принцип доступности в обучении вытекает из требований учета возрастных и индивидуальных особенностей детей дошкольного возраста. Он лежит в основе составления учебных планов и программ.
Принцип доступности требует, чтобы объем и содержание предлагаемого воспитателем материала были по силам воспитанникам, соответствовали уровню их умственного развития и имеющемуся у них запасу знаний, умений и навыков.
Реализация принципа доступности в развитии математических представлений предполагает выполнение следующих дидактических условий: а) следовать в обучении от простого к сложному; б) от легкого к трудному; в) от известного к неизвестному. [16]
Отсюда следует, что строгое соблюдение в обучении принципа систематичности и последовательности предопределяет успешную реализацию принципа доступности.
Принцип доступности в дошкольном образовании привлекает к себе особое внимание также в связи с проблемой индивидуального подхода к воспитанникам в условиях массового обучения в детском саду.
Принцип сознательности, активности и самостоятельности
Данный принцип заключается в целенаправленном активном восприятии изучаемых явлений, их осмыслении, творческой переработке и применении. Он вытекает из целей и задач дошкольного образования, а также из особенностей процесса обучения, требующего осмысленного и творческого подхода к изучаемому материалу.
Реализация принципа сознательности, активности и самостоятельности в обучении предполагает выполнение следующих условий:
а) соответствие познавательной деятельности детей закономерностям процесса учения;
б) познавательная активность воспитанников в процессе занятия;
в) осознание дошкольниками процесса приобретения знаний, умений и навыков;
г) овладение детьми дошкольного возраста методами умственной работы в процессе познания нового.
Сознательность понимается в дидактике как овладение учащимися данными науки, учебным материалом, осмысление его, умение пользоваться полученными знаниями на практике в новых условиях, превращение знаний в убеждения, в руководство к действию. [5]
Принцип наглядности
Теоретическое обоснование принципу наглядности впервые было дано чешским педагогом Я.А. Коменским, который выдвинул требование учить людей познавать самые вещи, а не только чужие свидетельства о них.
Принцип наглядности вытекает из сущности процесса восприятия, осмысления и обобщения детьми изучаемого материала.
Говоря о значении принципа наглядности и о его роли в процессе учебного познания, дидактика утверждает, что наглядность является исходным моментом обучения основам математических знаний главным образом в дошкольном возрасте и в младших классах.
Наглядность применяется и как средство познания нового, и для иллюстрации мысли, и для развития наблюдательности, и для лучшего запоминания материала. Средства наглядности используются на всех этапах процесса обучения: при объяснении нового материала воспитателем, при закреплении знаний, формировании умений и навыков, при выполнении самостоятельных заданий, при контроле усвоения учебного материала.
Принцип наглядности, по выражению Я.А. Коменского, является "золотым правилом дидактики". Он требует сочетания наглядности и мысленных действий, наглядности и слова. [1]
Принцип индивидуального подхода
Повышение эффективности обучения непосредственно связано с тем, насколько полно учитываются особенности каждого ребенка. Важной индивидуальной особенностью детей, в том числе и дошкольного возраста, является их способность к усвоению знаний.
Как показали многочисленные психолого-дидактические исследования, если уровнять многие факторы, влияющие на уровень усвоения новых знаний, а именно: обеспечить одинаковый исходный минимум знаний у всех воспитанников, положительное отношение их к занятию, желание как можно лучше усвоить материал, тщательно разработать методику введения нового материала, то, несмотря на равенство этих условий, новые знания будут усвоены по разному.
Следует заметить, что изучение разных сторон мыслительной деятельности позволило психологам сделать предположение о том, что не всякое усвоение знаний означает сдвиг в умственном развитии учащегося. Этот сдвиг происходит тогда, когда обучение обеспечивает овладение не только содержанием знаний, но и методами, способами их приобретения, благодаря чему дети могут самостоятельно приобретать новые знания. [11]
Отмеченные выше явления, имеющие место в развитии математических представлений дошкольников, показали невозможность создать в обучении систему, равно оптимальную для каждого воспитанника. Это обстоятельство привело к необходимости реализации в обучении принципа индивидуального подхода к каждому ребенку.
Таким образом, с учетом всего вышеперечисленного, уверенно можно говорить о том, что прочное и сознательное усвоение элементарных математических представлений детьми дошкольного возраста возможно лишь в случае применения в организации занятий по развитию математических представлений общедидактических принципов. [13]
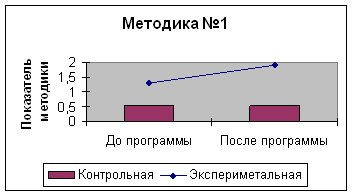
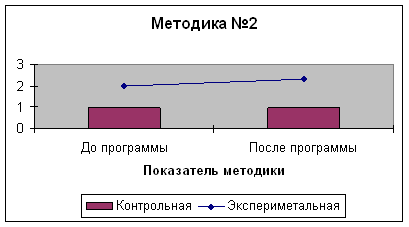
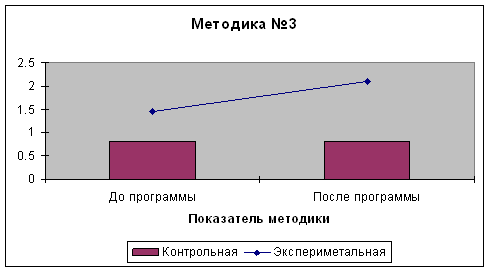
II. Экспериментальная работа по применению общедидактических принципов в организации занятий по развитию математических представлений в ДОО
Похожие работы
... развития должны иметь право выбрать свой путь: принимать участие в жизни общества, либо предпочесть защищенность и уединение. 1.5 Коррекционная направленность воспитания и обучения детей с задержкой психического развития Вся деятельность специального дошкольного учреждения базируется на соблюдении основополагающих принципов и подходов к вопросам изучения, воспитания и обучения детей ...
... характеристику основных знаний умений и навыков по данной специальности. Тифлопедагог дошкольного образовательного учреждения является ведущим специалистом, координирующим и направляющим коррекционно-педагогическую работу. В общем коррекционно-педагогическом процессе, осуществляемом в детском саду для детей с нарушением зрения, специальные коррекционные занятия тифлопедагога играют роль про ...
... адаптация открывает «особым» детям возможность активного участия в общественной жизни.[11; с. 192] 2.3 Создание условий для успешного формирования социальной адаптации умственно-отсталых детей дошкольного возраста С поступлением умственно отсталого ребенка в дошкольное учреждение в его жизни происходит множество изменений: строгий режим дня, отсутствие родителей в течение 9 и более часов, ...
... обследования ребенку предъявляются единые требования в семье и в дошкольном учреждении. § 2. Социально-проблемная ситуация как метод формирования социальной адаптации у детей младшего дошкольного возраста с нарушением интеллекта Проблемное обучение - особый тип обучения, в процессе которого учащиеся усваивают знания и учатся их применять не только в сходных ситуациях, не только в более или ...

0 комментариев