Повышение уровня умения самостоятельно применять полученные на занятиях математические знания в условиях дидактической игры (формирующий эксперимент)

2.2 Повышение уровня умения самостоятельно применять полученные на занятиях математические знания в условиях дидактической игры (формирующий эксперимент)

Для повышения уровня нами была разработана система по использованию дидактических игр для умения применять на практике полученные на занятиях математические знания.

Для различения количественного счета детям были предложены игры «Зоопарк» (Приложение 3); «Бензозаправочная станция». В последствии на основе этих игр дети самостоятельно организовывали игры «Аэропорт», «Магазин».

Педагоги поощряли детскую инициативу, поддерживали радостную атмосферу, старались создать интересную перспективу игры на следующий день. Дети предлагали поиграть в «Хлебзавод», «Столовую», «Детский сад» и другие игры, которые предоставляют огромные возможности применить и закрепить полученные на занятиях по математике знания и умения.

В содержании математических знаний и умений входит измерение. Введение в программу измерения непрерывных величин (протяженностей, массы, объемов жидкости и вместимости сосудов), использование для измерения условных мер разного размера помогает детям уяснить новое значение числа как выражения отношения одной величины к другой, принятой за единицу меры.

Многие профессии взрослых, которые доступны пониманию детей (например, швея, столяр, доярка, продавец и др.), основаны на измерении. Оно является необходимым средством выполнения различных трудовых процессов. Детям было предложено воспроизвести в сюжетно-дидактических играх действия людей разных профессий. Для проявления самостоятельной познавательной деятельности дети выбрали следующие игры: «Швейная фабрика», «Молочная ферма».

Выполняя разные роли в игре «Мебельная мастерская» (Приложение 5), дети измеряют протяженности, следя за точностью работы. Удовлетворяется желание всех детей осуществлять процесс измерения, не ожидая очереди для работы в мастерской. Дошкольники выбирают роли в соответствии со своими, интересами. Измерение включается и в другие игры. Так, жильцам одной квартиры привозят мебель, и, прежде чем ее расставить, мальчики измеряют длину простенка и ширину шкафа (игра «Новоселье»). Диспетчеры устанавливают маршруты поездов и теплоходов, следят за временем их отправления, измеряют расстояние от одной станции до другой (игра «Транспорт»). Кто-то из ребят предложил построить жилой район. Так началась игра «Строительство». И вот уже появились первые высотные дома. Строитель Алеша комментировал результаты своего труда строками из стихотворения С. Баруздина «Кто построил этот дом?».

Бетонщики в это время сооружали новую дорогу. Двое мальчиков – Андрей и Толик – решили провести разделительную линию и расставили дорожные знаки. С помощью условных мерок (линеек) они начали измерять длину и ширину дороги. Это привлекло внимание еще троих детей. Все дружно трудились, и вскоре на дороге появилась разделительная линия белого цвета, дорожные знаки для пешеходов и транспорта.

В процессе работы по повышению уровня умения применять полученные математические знания в процессе дидактических игр также были использованы настольно-печатные игры (Приложение 6) и игры с «жизненным» дидактическим материалом (Приложение 7).

Одновременно с дополнительным введением в самостоятельную деятельность детей дидактических игр продолжались занятия по формированию элементарных математических представлений.

В обстановке группы была создана атмосфера, которая побуждала детей использовать свои знания и умения в самостоятельной игровой деятельности.

В уголке группы были размещены различные игры-лото: «Что похоже на данную фигуру?»; «Найди на один меньше».

С родителями детей данной группы была проведена консультация на тему: «Специфика развития математических способностей» (приложение 8)

Было подготовлено и сделано выступление на педагогическом совете ДОУ на тему: «Познавательная деятельность детей в ДОУ». (Приложение 9)

Заключительным этапов формирующего эксперимента было проведение математического досуга с участием детей всей подготовительной группы. (Приложение10)

2.3 Проверка эффективности проделанной работы на формирующем этапе эксперимента (контрольный эксперимент)

Для определения эффективности проделанной нами работы на формирующем этапе эксперимента был использован следующий диагностический материал.

Задание 1.

Перед каждым ребенком положили 2 листа бумаги. На одном с нарисованы в ряд кружочки, на другом изображены семена.

Экспериментатор:

Это болотце с кочками, по которым будут скакать лягушки. Лягушонок (он перед вами) должен прискакать на седьмую кочку и остаться на ней. Подумайте, как надо считать, чтобы лягушонок попал на седьмую кочку.

Экспериментатор: Подвиньте листочки, на которых нарисованы семена. Самые первые ростки появились из четвертого и шестого семени. Нарисуйте на этих семенах ростки.

Задание 2 – установление связей и отношений между числами натурального ряда.

Экспериментатор. Сейчас поиграем в игру «Угадай числа». Я буду называть вам числа, а вы, взяв нужную карточку с цифрами, покажите, какое число больше (меньше) названного на 1 (называются числа 5, 6, 7). Итак:

какое число стоит до 7? после 7? (Дети показывают карточки с цифрами в и 8.) угадайте, какое число больше 5 и меньше 7. (Дети показывают цифру 6.) угадайте, какое число больше 7 и меньше 9. (Дети показывают цифру И.)

Задание 3 – состав числа из двух меньших.

На воротах, сделанных из фанеры, прикрепляется карточка с цифрой. У каждого ребенка имеется 1 карточка с одной из цифр от 1 до 9. В ворота может пройти та пара, у которой в сумме на карточках получается число, какое обозначено цифрой на воротах. Цифры меняются, и соответственно им ребенку каждый раз нужно найти себе в пару другого игрока с цифрой, которая вместе с его карточкой составит сумму, равную указанной на воротах. Каждая пара получает по 2 фишки.

Задание 4 – сохранение дискретных количеств.

Экспериментатор. Все вы, дети, любите играть в шашки. Но сегодня вы будете играть не так, как в настоящей игре. У каждого на столе 2 ряда черных и белых шашек (шашек одинаковое количество, расположены они параллельно). Каких шашек больше (меньше) или их поровну? Если шашек поровну, вы должны поднять квадрат красного цвета, если не поровну, то зеленого цвета. (Дети поднимают красные квадраты.)

Экспериментатор. А теперь поставьте черные шашки в столбик. Каких шашек больше (меньше) или их поровну? (Тем детям, которые поднимают красные квадраты, что означает: шашек поровну, их количество не изменилось, – вручают фишки.)

Задание 5 – счет единиц по мерке, равной нескольким частям, которые физически не объединяются.

Экспериментатор. Дети, вы любите кашу? Чтобы сварить вам на ужин вкусную кашу, повару нужна крупа. Но весы на кухне сломались, и он не смог узнать, сколько взять крупы. Помогите ему: у нас есть полиэтиленовые пакеты, в каждый пакет нужно насыпать по 2 больших бокала крупы.

Дети с удовольствием соглашаются помочь. Экспериментатор сообщает, что имеется, к сожалению, только 1 бокал, но перед каждым стоит маленькая чашка, 2 таких чашки составляют 1 бокал. Он демонстрирует, что в 1 бокал вмещаются 2 маленьких чашки крупы. Дети самостоятельно меряют крупу чашками и отдают мешочки повару. Правильно выполнившим задание члены жюри вручают фишки.

Задание 6 зависимость числа от величины мерки при неизменной величине объекта измерения.

У всех детей имеются одинаковые по длине ленты, но для их измерения воспитанники получают разные мерки.

Экспериментатор. Сколько раз уложилась мерка по длине ленты? Почему получились разные числа? (Дети объясняют.)

Ответы детей оценивались по бальной системе

0 баллов – ребенок не выполнил задание;

1          балл – ребенок выполнил задание частично;

2          балла – ребенок выполнил задание полностью.

Наибольшее количество баллов, которое мог бы набрать ребенок по результатам 6 заданий 12 баллов.

Результаты выполнения заданий в контрольном эксперименте приведены в Приложении 11.

Оценка результатов:

Высокий уровень – 10–12 баллов;

Средний уровень – 5–9 баллов;

Низкий уровень – 0–4 балла.

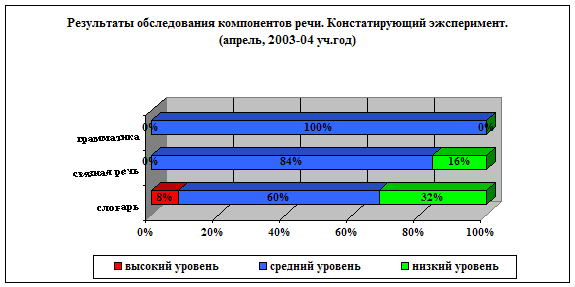
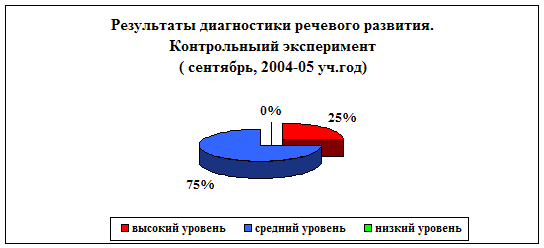
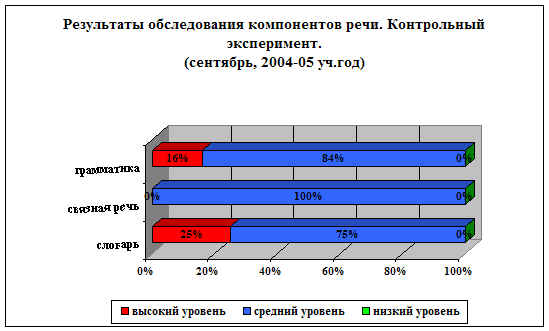
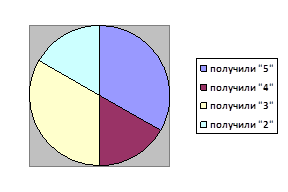
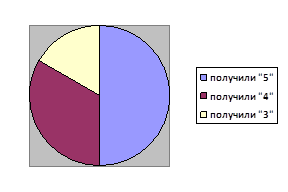
Сравнивая результаты констатирующего и контрольного этапов эксперимента (Таблица 1) видно, что у большинства детей наметилась положительная тенденции к повышению уровня умения самостоятельно применять полученные на занятиях математические знания в новых условиях.

Таблица 1. Динамика повышения уровня умения самостоятельно применять полученные математические знаний

№ п/п	Имя ребенка	Констатриующий эксперимент		Контрольный эксперимент		Прирост (в баллах)
		Общее кол-во баллов	Уровень	Общее кол-во баллов	Уровень
1	Алеша С.	5	С	8	С	3
2	Андрей К.	5	С	9	С	4
3	Аня М.	6	С	10	В	4
4	Вика Д.	5	Н	8	С	3
5	Вика К.	4	Н	7	С	3
6	Женя Б.	2	Н	8	С	6
7	Лена П.	4	Н	6	С	2
8	Данил С.	3	Н	5	С	2
9	Толик С.	3	Н	4	Н	1

Как видно из таблицы 3 детей (34%) остались на том же уровне, 1 ребенок (11%) повысил свой уровень до высокого, 4 ребенка (44%) повысили свой уровень до среднего и 1 реб-к (11%) остался на том же уровне (низком).

Наиболее наглядно это можно увидеть на сравнительной диаграмме (Рис/ 2).

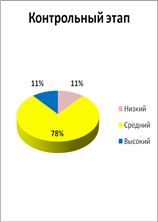
Рис. 2 Сравнительная диаграмма динамики повышения уровней умений по результатам констатирующего и контрольного этапов эксперимента

Анализ ответов детей на задания контрольного эксперимента свидетельствует о том, что большинство детей овладели программным материалом по математике и они могут применять эти знания при решении задач, сформулированных в ходе игры по-новому.

Большинство детей легко понимали смысл практических заданий, дети логично действовали и доказывали правильность своего ответа, ребята старались свободно ориентироваться в сложных зависимостях существующих между объектами измерения, мерами и числами., но к сожалению, это не удалось сделать Толе С, Жене Б.

Толик на вопросы задания № 2, сильно нервничал, путался в карточках и поэтому не смог дать правильного ответа.

Данил С. Проходя через ворота вместе с Леной П (задание 3) не смог показать второе правильное число из которого должна получиться сумма 8 (Лена показала число 3, а Данил 6).

Большинство детей (5 человек) легко справились с 4 заданием, а у 4 детей это задание вызвало небольшое затруднение. Так, Вика К. не смогла определить количество шашек на столе, девочка сказала, что белых шашек больше чем черных (Правильный ответ поровну).

С 5 заданием справились всего 3 детей. 6 детей не смогли использовать условную мерку: дети пересыпали в пакет маленькие чашки, вместо того, чтобы 2 маленькие чашки высыпать в один бокал.

Таким образом, результаты контрольного эксперимента свидетельствуют о эффективности проделанной нами работы на формирующем этапе эксперимента. Необходимо отметить то, что по окончании нашего исследования работа по использованию дидактических игр в самостоятельной познавательной деятельности детей педагогами ДОУ должна продолжаться, так как не все дети умеют самостоятельно применять полученные на занятиях по математике знания в новых условиях.

Заключение

В дошкольном возрасте закладываются основы знаний, необходимых ребенку в школе. Математика представляет собой сложную науку, которая может вызвать определенные трудности во время школьного обучения. К тому же далеко не все дети имеют склонности и обладают математическим складом ума, поэтому при подготовке к школе важно познакомить ребенка с основами счета.

И родители, и педагоги знают, что математика – это мощный фактор психического развития ребенка, формирования его познавательных и творческих способностей. Самое главное – это привить ребенку интерес к познанию. Для этого занятия и повседневная деятельность детей должны проходить в увлекательной игровой форме.

Благодаря играм удаётся сконцентрировать внимание и привлечь интерес даже у самых несобранных детей дошкольного возраста. В начале их увлекают только игровые действия, а затем и то, чему учит та или иная игра. Постепенно у детей пробуждается интерес и к самому предмету обучения.

Таким образом, в игровой форме прививание ребенку знания из области математики, научит его выполнять различные действия, разовьет память, мышление, творческие способности. В процессе игры дети усваивают сложные математические понятия, учатся считать, читать и писать, а в развитии этих навыков ребенку помогают близкие люди – его родители и педагог.

Формированию у ребенка математических представлений способствует использование разнообразных дидактических игр. Такие игры учат ребенка понимать некоторые сложные математические понятия, формируют представление о соотношении цифры и числа, количества и цифры, развивают умения ориентироваться в направлениях пространства, делать выводы.

При использовании дидактических игр широко применяются различные предметы и наглядный материал, который способствует тому, что занятия проходят в веселой, занимательной и доступной форме.

Логические игры математического содержания воспитывают у детей познавательный интерес, способность к творческому поиску, желание и умение учиться. Необычная игровая ситуация с элементами проблемности, характерными для каждой занимательной задачи, всегда вызывает интерес у детей.

Занимательные задачи способствуют развитию у ребенка умения быстро воспринимать познавательные задачи и находить для них верные решения. Дети начинают понимать, что для правильного решения логической задачи необходимо сосредоточиться, они начинают осознавать, что такая занимательная задачка содержит в себе некий «подвох» и для ее решения необходимо понять, в чем тут хитрость.

Анализ теоретических положений и методических выводов позволил предоставить результаты опытно-экспериментальной работы, проведённой на базе ДОУ № 4 комбинированного вида г. Октябрьска по повышению уровня умения самостоятельно применять полученные на занятиях по математике знания в условиях дидактической игры. Была прослежена динамика изменения уровня умения в процессе экспериментальной работы. При прочих равных условиях на начальном этапе эксперимента уровень развития детей был приблизительно одинаков. Анализ результатов до и после формирующего эксперимента свидетельствует об эффективности разработанной нами методики совершенствования работы. Результаты детей улучшились. Один ребенок достиг высокого уровня умения, также возросли показатели среднего уровня с 67,7% до 78%, но к сожалению остался один ребенок на прежнем низком уровне.

В процессе работы были замечены такие изменения: дети стали считать предметы на расстоянии, взором, вслух произнося числительные и пользуясь указательным жестом. Дети стали более активными, самостоятельными и внимательными к действиям счета, стали рассуждать, доказывать. Некоторые заметно расширили свои знания, за счет общения в игре с другими детьми, они не только стали решать задачи без всякой наглядной опоры, но и самостоятельно придумывать новые игры со счетными действиями, привлекая к ним и других детей.

Разумеется, данное исследование не претендует на достаточно полное, и вопрос остаётся актуальным. Однако в плане повышения роль дидактических игр в самостоятельной познавательной деятельности детей переработаны известные методические аспекты и адаптированы для детей старшего дошкольного возраста в конкретных условиях детского учреждения.

Исходя из анализа опытно-экспериментальной работы, можно прийти к выводу, что гипотеза о том, что роль дидактических игр в самостоятельной познавательной деятельности детей будет значимой, если педагогическая работа по их использованию будет носить целенаправленный и планомерный характер, если создать такие педагогические условия:

1.         Систематически давать детям возможность использовать свои знания на практике;

2.         Способствовать самореализации детей в различных видах игровой деятельности;

3.         Развивать познавательную деятельность детей, через нетрадиционный подход к использованию дидактических игр в педагогической деятельности;

Список используемой литературы

1.    Бондаренко А.К. Дидактические игры в детском саду. – М.: Просвещение, 1991. – 160 с.

2.    Болотин Л.Р., Т.С. Комарова, С.П. Баранов. Дошкольная педагогика – М.: Академия, 1997 – 240 с.

3.    Венгер Л.А, Мухина В.С. Психология. – М.: Просвещение, 1988–326 с.

4.    Возрастные возможности усвоения знаний. / Под ред. Д.Б. Эльконина и В.В. Давыдова – М.: Изд. «Просвещение», 1966. – 442 с.

5.    Воспитателю о детской игре.: Пособие для воспитателей детского сада/ Под ред. Т.А. Марковой. – М.: Просвещение, 1982. – 128 с., ил.

6.    Выготский Л.С. Избранные психологические исследования. Мышление и речь. Проблемы психологического развития ребенка – М.: Изд. Акад. пед. Наук РСФСР, 1956. – 520 с.

7.    Гринченко И.С. Игра в теории, обучении, воспитании и коррекционной работе. Учебно-методическое пособие – М.: «ЦГЛ», 2002. – 80 с.

8.    Дидактические игры и занятия с детьми раннего возраста: Пособие для воспитателей детского сада/ Е.В. Зворыгина, Н.С. Карпинская, И.М. Кононова и др.; Под ред. С.Л. Новоселовой. – 4-е изд., перераб. – М.: Просвещение, 1985. – 144 с., 4 л. ил.

9.    Дневник воспитателя: развитие детей дошкольного возраста. / Под ред. О.М. Дьяченко, Т.В. Лаврентьевой – М.: «Издательство ГНОМ и Д», 2000. – 144 с.

10.  Дурова Н.В., Новикова В.П. Ступеньки к познанию./ Худ. Ю.В. Богатова. – СПб.: ДЕТСТВО-ПРЕСС, 2003. – 56 с.: ил.

11.  Запорожец А.В. Значение ранних периодов детства для формирования детской личности. Принцип развития в психологии. М. 1978, с. 243 – 267

12.  Игры и упражнения по развитию умственных способностей у детей дошкольного возраста: Кн. для воспитателя дет. cада. – М.: Просвещение, 1989. – 127 с.: ил.

13.  Коломенских Я.Л., Панько Е.А. Детская психология., Мн. «Университетское», 1988, – 223 с.

14.  Леушина А.М. Формирование элементарных математических представлений у детей дошкольного возраста – М.: Просвещение, 1974–366 с.

15.  Метлина Л.С. Занятия по математике в детском саду - М.: Просвещение, 1985–219 с.

16.  Перова М.Н. Дидактические игры и упражнения по математике для работы с детьми дошкольного и младшего школьного возраста: Пособие для учителя. – 2-е изд., перераб. – М.: Просвещение, Учебная литература, 1996. – 144 с.: ил.

17.  Сорокина А.И. Дидактические игры в детском саду: (Ст. группы). Пособие для воспитателей дет. сада. – М.: Просвещение, 1982. – 96 с.

18.  Соколова Е., Митрохина М. Занимательная математика//Ребенок в детском саду-2005– № 4 -40–46 с.

19.  Столяр А.А. Формирование элементарных математических представлений у дошкольников-М.: Просвещение, 1988–300 с.

20.  Смоленцева А.А. Сюжетно-дидактические игры с математическим содержанием. - М.: Просвещение, 1987–97 с.

21.  Урунтаева Г.А. Дошкольная психология: Учеб. пособие. – М.: Академия, 1996. – 336 с.

22.  Щербакова Е.И. Методика обучения математике вы детском саду. – М.: Академия, 2000–270 с.