Умножили на неизвестное число и получили 27. Найти неизвестное число

9 умножили на неизвестное число и получили 27. Найти неизвестное число.

7) Нахождение делимого по известным делителю и частному.

Неизвестное число разделили на 9 и получили 4. Найти неизвестное число.

8) Нахождение делителя по известным делимому и частному.

24 разделили на неизвестное число и получили 6. Найти неизвестное число.

К третьей группе относятся задачи, при решении которых раскрываются понятия разности и кратного отношения. К ним относятся простые задачи, связанные с понятием разности (6 видов), и простые задачи, связанные с понятием кратного отношения (6 видов).

1) Разностное сравнение чисел или нахождение разности двух чисел (I вид).

Один дом построили за 10 недель, а другой за 8 недель. На сколько недель больше затратили на строительство первого дома?

2) Разностное сравнение чисел или нахождение разности двух чисел (II вид).

Один дом построили за 10 недель, а другой за 8. На сколько недель меньше затратили на строительство второго дома?

3) Увеличение числа на несколько единиц (прямая форма). Один дом построили за 8 недель, а на строительство второго дома затратили на 2 недели больше. Сколько недель затратили на строительство второго дома?

4) Увеличение числа на несколько единиц (косвенная форма).

На строительство одного дома затратили 8 недель, это на 2 недели меньше, чем затрачено на строительство второго дома. Сколько недель затратили на строительство второго дома?

5) Уменьшение числа на несколько единиц (прямая форма).

На строительство одного дома затратили 10 недель, а другой построили на 2 недели быстрее. Сколько недель строили второй дом?

6) Уменьшение числа на несколько единиц (косвенная форма).

На строительство одного дома затратили 10 недель, это на 2 недели больше, чем затрачено на строительство второго дома. Сколько недель строили второй дом?

Задачи, связанные с понятием кратного отношения.(не приводя примеры)

1) Кратное сравнение чисел или нахождение кратного отношения двух чисел (I вид). (Во сколько раз боль­ше?)

2) Кратное сравнение чисел или нахождение кратного от­ношения двух чисел (II вид). (Во сколько раз мень­ше?)

3) Увеличение числа в несколько раз (прямая форма).

4) Увеличение числа в несколько раз (косвенная форма).

5) Уменьшение числа в несколько раз (прямая форма).

6) Уменьшение числа в несколько раз (косвенная форма).

Здесь названы только основные виды простых задач. Однако они не исчерпывают всего многообразия задач.

Порядок введения простых задач подчиняется содержанию программного материала. В I классе изучаются действия сложения и вычитания и в связи с этим рассматриваются простые задачи на сложение и вычитание. Во II классе в связи с изучением действий умножения и деления вводятся простые задачи, решаемые этими действиями.

 

ГЛАВА 2. Моделирование как средство формирования умения решать задачи 2.1. Виды моделирования. Графическое моделирование как основное средство

Глубина и значимость открытий, кото­рые делает младший школьник, решая задачи, определяется характером осущест­вляемой им деятельности и мерой ее освоения, тем, какими средствами этой деятельности он владеет. Для того чтобы ученик уже в начальных классах мог выделить и освоить способ решения широкого класса задач, а не ограничи­вался нахождением ответа в данной, конкретной задаче, он должен овла­деть некоторыми теоретическими знания­ми о задаче и, прежде всего, о ее структуре.

Известный отечественный психолог А.Н. Леонтьев писал: «Актуально сознается только то содержание, которое является предметом целенаправленной активности субъекта». Поэтому, чтобы структура задачи стала предметом анализа и изучения, необходимо отделить ее от всего несущественного и представить в таком виде, который обеспечивал бы необходимые действия. Сделать это мож­но путем особых знаково-символических средств — моделей, однозначно отобра­жающих структуру задачи и достаточно простых для восприятия младшими школьниками.

В структуре любой задачи выделяют:

1. Предметную область, т. е. объекты, о которых идет речь в задаче.

2. Отношения, которые связывают объекты предметной области.

3. Требование задачи.

Объекты задачи и отношения между ними составляют условие задачи. Напри­мер, в задаче: «Лида нарисовала 5 домиков, а Вова - на 4 домика больше. Сколько домиков нарисовал Вова?» — объектами являются:

1) количество домиков, нарисованных Лидой (это известный объект в задаче);

2) количество домиков, нарисованных Вовой (это неизвестный объект в задаче и согласно требованию искомый).

Связывает объекты отношение «больше на».

Структуру задачи можно представить с помощью различных моделей. Но преж­де, чем сделать это, уточним некоторые вопросы, связанные с классификацией моделей и терминологией.

Все модели принято делить на схема­тизированные и знаковые.

В свою очередь, схематизированные модели бы­вают вещественными (они обеспечивают физическое действие с предметами) и графическими (они обеспечивают графи­ческое действие).

К графическим моде­лям относят рисунок, условный рисунок, чертеж, схематический чертеж (или схему).

Знаковая модель задачи может выпол­няться как на естественном языке (т. е. имеет словесную форму), так и на математическом (т. е. используются сим­волы).

Например, знаковая модель рассматри­ваемой задачи, выполненная на естест­венном языке,— это общеизвестная крат­кая запись:

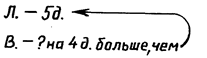
Знаковая модель данной задачи, вы­полненная на математическом языке, имеет вид выражения 5+4.

Уровень овладения моделированием определяет успех решающего. Поэтому обучение моделированию занимает особое и главное место в формировании умения решать задачи.

Лавриненко Т.А. предлагает следующие приемы предметного моделирования простых задач на сложение и вычитание: с дочислового периода начинать выполнять практические упражнения по всем видам задач, объясняя полученный результат и выборочно зарисовывать в тетради.

-     Положите три красных кружка, а ниже положите 5 синих кружков. Сколько всего кружков вы положили?

	3	8
	5

-     Положите 6 квадратов, а теперь 2 уберите. Сколько осталось квадратов? 6

2

 

-     Положите три круга, а внизу положите на 2 квадрата больше. Сколько вы положили квадратов? Как вы выкладывали квадраты?

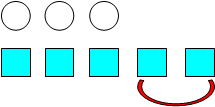3

5

2

-     Положите 7 желтых треугольников, а внизу красных треугольников положите на 3 меньше, чем желтых. Сколько красных треугольников вы положили? Как догадались?

7

4

3

-     Положите 5 квадратов. Ниже положите 3 круга. Чего больше? На сколько больше? Как вы догадались?

2

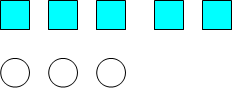5

3

После знакомства со знаками «+» и «- » необходимо продолжить выполнение практических упражнений, применяя графическое моделирование, вводя тексты задач и выбирая нужное действие.

-     На ветке сидело 8 птичек (положите 8 палочек), 3 птички улетели (отодвинули 3 палочки). Сколько птичек осталось? Какое действие выберем? (Отодвинули, значит, «вычитание»).

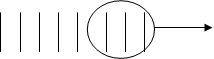8-3=5 (пт.)

-     У Коли 5 машинок (положите 5 квадратиков), а у Сережи на две машинки меньше (выложите машинки Сережи кружочками.) Сколько машинок у Сережи? Какое действие выберем? Почему? (Мы закрыли два квадрата, а сколько осталось – столько выложили кружков. Убрали 2 квадрата, значит, выполнили действие «вычитание»).

5-2=3 (м.)

2

 

Учим правило «На… меньше – делаем вычитание»

-     У Кати 6 красных шаров (выкладываем 6 красных кружков) и 4 синих (выкладываем внизу 4 синих кружка). На сколько у Кати красных шаров больше, чем синих?

-     Как найдем на сколько больше красных шаров? (Нужно из красных отодвинуть столько, сколько синих, узнаем на сколько больше красных шаров).

-     Какое действие выберем? (Мы отодвинули шары, значит, действие «вычитание»).

6-4=2 (ш).

?

 

Учим правило «Чтобы сравнить, на сколько одно число больше другого, нужно из большего числа вычесть меньшее».

Итак, целенаправленная работа по формированию приемов умственной деятельности начинается с первых уроков математики при изучении темы “Отношения равенства-неравенства величин”. Действуя с различными предметами, пытаясь заменить один предмет другим, подходящим по заданному признаку, дети выделяют параметры вещей, являющиеся величинами, т.е. свойства, для которых можно установить отношения равно, неравно, больше, меньше. В контексте задач дети знакомятся с длиной, массой, площадью, объемом. Полученные отношения моделируются сначала с помощью предметов, графически (отрезками), а затем - буквенными формулами.

На первых же уроках нужно познакомить детей с прямой и кривой линией, а затем с понятием отрезка и научить чертить отрезки по линейке. Для этого можно выполнить упражнение следующего вида:

 

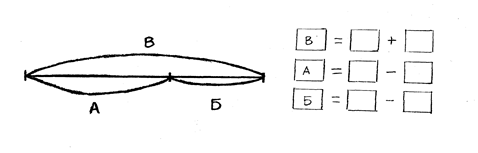
После того как дети хорошо разберутся в понятии “задача”, можно учить их составлять задачи по картинкам, причем все виды задач. Здесь полезно применять чертежи и схематические рисунки, блок-схемы, моделирование с помощью отрезков, таблиц и матриц.

Графические модели и таблицы позволяют сравнивать пары понятий: левая – правая, верхняя – нижняя, увязывать пространственную информацию (правая – левая) с информацией меры (широкая - узкая, короткая - длинная) тем самым формируя умение решать задачи. Примером может служить таблица:

	Короткая (левая)	Длинная (правая)
Широкая (верхняя)
Узкая (нижняя)

 

В беседе со школьниками по этой матрице следует задавать противопо-ложные по содержанию вопросы.

Вопрос: какая лента нарисована в правой нижней клетке? Ответ: длинная и узкая. Вопрос: где нарисована короткая и широкая лента? Ответ: в левой верхней клетке.

Табличные примеры удобны для быстрого решения примеров, информационно связанных друг с другом (рис.3). Так, например, заполняя клетки таблицы, школьники должы обратить внимание на совпадение парных сумм, например: 35+47=45+37=82.

	А + В
А В	43	45	47	49
33
35
37
39

 

2.2. Обучение решению задач на движение с помощью схематического моделирования

На подготовительном этапе на основе движущихся моделей дети должны уяснить что значит двигаться навстречу друг другу и в противоположных направлениях. Необходимо познакомить детей с элементами чертежей к задачам на движение и научить их вычерчивать по условию задачи.

24 м ?, на 8 м <

? м

После такого предварительного знакомства вводится понятие "скорость". Беседа начинается с того, что есть предметы движущиеся и не движущиеся (дети приводят примеры). Опираясь на жизненный опыт детей, выясняем, что одни предметы движутся быстрее, другие медленнее.

Открываем таблицу на доске:

Пешеход — 5 км за 1 час	5 км/ч
Автомобиль — 80 км за 1 час	80 км/ч
Ракета — 6 км за 1 сек.	6 км/с
Черепаха — 5 м за 1 мин.	5 м/мин

В этом случае говорят, что скорость пешехода 5 км в час (показываем запись 5 км/ч) и т. д.

Скорость движения — это расстояние, которое проходит движущийся предмет за единицу времени (за 1 час, за 1 минуту, за 1 секунду).

- Проверим, как вы меня поняли. Скорость поезда 70 км/ч. Что это означает? (Поезд проезжает 70 км за 1 час.)

- Скорость мухи — 5 м/с — ?

- Скорость африканского страуса — 120 км/ч — ?

Задача. Велосипедист был в пути 3 ч и проехал за это время 36 км. В течение каждого часа он проезжал одинаковое расстояние. Сколько километров проезжал велосипедист в каждый час?

36 ч

Пояснить, что чёрточки означают количество часов.

36 : 3 = 12 (?)

Мы нашли, сколько километров проезжал велосипедист за каждый час, т. е. за 1 час или за единицу времени. Что же это за величина? (Скорость.) Как обозначим единицу измерения скорости? (км/ч)

36 : 3 = 12 (км/ч) V = S : t

 ^{скор .расст. вр.}

 

Вывешивается формула и заучивается правило. На следующих уроках вводятся два других правила. После того, как дети выучат правила, задачи решаются в два и более действия; используется краткая запись в виде чертежа или таблицы.

Необходимо познакомить детей с понятием "общей скорости" (скорость сближения или удаления) и пояснить, что использование понятия "общая скорость" упрощает решение задач.

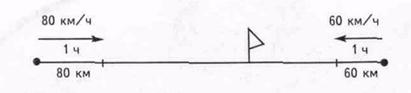
рис.2.

60 + 80 = 140 (км/ч) — общая скорость. На 140 км сблизятся машины за 1 час.

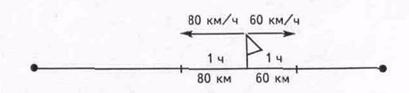
На 140 км удалились машины друг от друга за 1 час.

Чтобы дети уяснили решение задач через "общую скорость", нужно первые задачи разобрать от данных к вопросу.

— Известно "общее" расстояние 390 км и известно время — 3 ч. Что можно найти, зная расстояние и время?

— Если дано "общее" расстояние, то какую скорость мы найдём? (Найдём общую скорость.)

— Теперь, зная "общую скорость" и скорость первого автомобиля, что можно найти? (Скорость второго автомобиля.)

— Ответили мы на вопрос задачи? (Да.)

Весьма поучительно решение следующей четверки задач, исчерпывающих все возможные комбинации направлений движения двух тел относительно друг друга (рис.7). Вопрос для всех задач общий: через сколько секунд А и В окажутся рядом? Итак, дана задача: «Между двумя точками А и В имеются две дороги, длинная — 160 м и короткая — 80 м. Из этих точек движутся два велосипедиста со скоростями 5 и 3 м в секунду. Через сколько секунд они окажутся рядом? (Рассмотреть все возможные случаи.)»

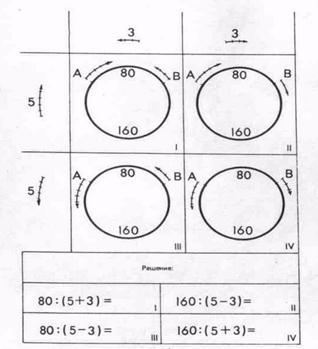
Решение задачи удобно изобразить в матрице с двумя входами.

Подобная четверка задач позволяет рассмотреть исчерпывающим образом математическую ситуацию, перебирая все возможные сочетания направлений движения двух тел. При таком оформлении четверки задач информация о направлении движения передается на нескольких кодах: по горизонтальному входу матрицы показаны скорости велосипедиста А, по вертикальному входу матрицы показаны скорости велосипедиста В. Эти же скорости изображены и на самих рисунках в матрице. По этой схеме удобно проводить обучающую беседу, позволяющую добыть дополнительную информацию об изучаемом.

Вопрос. В каких клетках изображено движение в противоположных направлениях (навстречу»)? Ответ. Движение «навстречу» изображено в клетках правой диагонали (I и IV). Вопрос. В каких клетках изображено движение в одном направлении («вдогонку»)? Ответ. Движение вдогонку изображено в клетках левой диагонали (11 и III). Вопрос. Сравните задачи (II и III). В каком случае быстрее нагонит один велосипедист другого? Почему? Ответ. В первом случае, так как в этом случае первоначальное расстояние между велосипедистами – 80 м. во втором случае – больше (160 м).

Мы описали беседу, основанную на качественных сравнениях:

(1—11), (IV—III), (I—IV). Однако в таком анализе можно пойти значительно дальше, проникая в глубинные связи, которые при обычной практике обучения на основе одинарных задач являются для мышления школьника недоступными. В процессе дополнительного обсуждения можно извлечь новые сведения.

Вопрос. Какова скорость сближения велосипедистов в (11) и (III) случаях? Ответ. Скорости сближения равные, так как в обоих случаях движение совершается вдогонку. Скорость сближения здесь равна 5+3=8 (м) за каждую секунду Вопрос. Через сколько секунд произойдет первая встреча в первой и четвертой задачах? Ответ. 80:2=40 (с); 160:2=80 (с). Вопрос. Через сколько секунд будут происходить последующие встречи? Через различное время или одно и то же время? Почему? Ответ. После первой встречи условия задач оказываются одинаковыми: в обоих случаях быстрейший должен нагнать медленного велосипедиста через (160+80):2=120 (с). Вопрос. Почему же здесь расстояние выросло до 160+80=240 (м)? Ответ. Потому что между данными двумя велосипедистами в момент встречи расстояние равно нулю (0 метров). Однако при дальнейшем движении между быстрейшим и медленным оказывается весь круговой путь (160+80=240). Вопрос. Через сколько секунд будут происходить последующие встречи в 1 и IV задачах? Ответ. (160+80): (5+3)= =240:8=30 (с).

Мы видим, что решение сматрицированной задачи, состоящей из четырех попарно связанных случаев, становится особым видом укрупненного упражнения, т.е. некоторым сочинением на математическую тему «Задачи на движение».

ЗАКЛЮЧЕНИЕ

Как научить детей решать задачи? С психолого-методической точки зрения, по всей вероятности, необходимо организовать обучение с опорой на опыт дошкольников, на их предметно-действенное и  наглядно-образное мышление, необходимо формировать и развивать у учеников математические понятия на основе содержательного обобщения уже известных фактов.

Число математических понятий невелико. Школьный курс математики сводится к следующему: число, пространство, линия, поверхность, точка, функция, производная, вероятность, множество.

Целенаправленная работа по формированию приемов умственной деятельности должна начинаться с первых уроков математики при изучении темы «Отношения равенства-неравенства величин». Действуя с различными предметами, пытаясь заменить один предмет другим, подходящим по заданному признаку, дети должны научиться выделять параметры вещей, являющиеся величинами, т.е. свойства, для которых можно установить отношения равно, неравно, больше, меньше. В контексте задачи дети знакомятся с длиной, массой, площадью, объемом. Полученные отношения моделируются сначала с помощью предметов, графически (отрезками), а затем - буквенными формулами.

Наглядность задач необходима для их лучшего понимания, ощущения действительности и необходимости математики в повседневной жизни.

Кроме графических моделей для лучшего усвоения учебного материала необходимо в уроки математики вводить элементы истории, и чем раньше дети узнают что такое математика, как появилось число, отрезок, деньги и т.д., тем быстрее будет происходить расширение умственного кругозора учащихся и повышение их общей культуры, повысится интерес к изучению математики, углубится понимание изучаемого фактического материала.

В настоящее время широкое распространение получила система обучения разработанная под руко­водством Л.В.Занкова (СОЗ). Главным стержнем этой системы является достижение максимального резуль­тата в общем развитии школьников. Под общим развитием в систе­ме понимается развитие ума, воли, чувств, т.е. всех сторон психики ребенка.

Забота об общем развитии детей в процессе обучения по любо­му предмету является одной из характерных особенностей системы. Вдумчивая и творческая рабо­та учителей по системе показала, что при обучении математике открывается широкое поле деятельности для развития различных чувств - нравственных, эстетических, интеллек­туальных.

Ориентация процесса обучения на достижение высокого общего развития учащихся ведет к коренному пересмотру как общей линии в обучении математике, так и конкретных методических приемов, ис­пользуемых в нем.

При построении процесса обучения математике важнейшим в СОЗ считается вопрос о соотношении прямого и косвенного путей форми­рования знаний, умений и навыков, которые присутствуют в любой системе обучения.

Первый из них заключается в использовании большого количества заданий или упражнений, предусматривающих формирование опре­деленных знаний, умений и навыков по математике, которые выполня­ются на основе заданного образца или использования данного в гото­вом виде алгоритма решения, т.е. основным видом деятельности явля­ется репродуктивная деятельность. Такой путь нередко считается наи­более экономным, надежным при обучении математике.

Косвенный путь во главу угла ставит продвижение в развитии школьников, что требует продуктивной деятельности детей, исполь­зования их творческого потенциала при выполнении предлагаемых заданий. Такой процесс обучения строится на основе самостоятель­ного добывания знаний школьниками, ведет их по пути открытий. Здесь имеют место рассуждения, предположения, рассмотрение раз­ных точек зрения, отказ от предположений, выбор нового пути реше­ния, и т.п., т.е. имеет место истинный диалог между учителем и уче­никами, между самими учащимися. Нередко такой путь рассматри­вается как тормозящий формирование навыка, но это не так. Хотя на первом этапе формирования затрачивается более длительный отре­зок времени, в дальнейшем сформированный навык оказывается зна­чительно более стойким и легко восстановимым, чем при использо­вании прямого пути.

Системы обучения, ориентированные в первую очередь на приоб­ретение суммы знаний, умений и навыков, в основном используют пря­мой путь обучения, как приводящий к достаточно быстрому достиже­нию поставленной цели, косвенный же является вспомогательным и используется эпизодически, не оказывая существенного влияния.

Аргинская И.И. считает, что в системе обучения, направленной на продвижение детей в общем, развитии, основным является косвенный путь, прямой путь не исключается, но и он приобретает иной вид, иной характер, т.к. не существует отдельно, а становится органической частью общего на­правления на творчество детей.

Доктор педагогических наук П. Эрдниев и кандидат педагогических наук Б. Эрдниев предложили новую методическую систему укрупне­ния дидактических единиц (УДЕ). Президиум Академии педагогических наук СССР по предложе­нию Министерства просвещения РСФСР провел решающий экспе­римент по проверке эффективности УДЕ. В этих целях составленные программы и опытные учебники по математике для начальных классов испытывались в течение трех лет (1977–1980) в экспери­ментальной школе № 82 АПН СССР (пос. Черноголовка Ногин­ского района Московской области). Исследованием был охвачен 21 контрольный и экспериментальный класс (всего в этих классах было 745 учащихся).

Сравнение показателей успешности усвоения знаний прово­дилось по текстам, подготовленным как руководителем иссле­дования, так и Научно-исследовательским институтом содержа­ния и методов обучения АПН СССР, а также Программно-ме­тодическим управлением Министерства просвещения РСФСР.

В решении президиума АПН СССР от 28 VIII 1980 г. по итогам трехлетнего испытания программ и учебников была одобре­на технология укрупнения знаний, а созданная методическая система была рекомендована к внедрению в школьную учебную практику.

В постановлении президиума АПН СССР по итогам этого иссле­дования было записано: «Подтверждена целесообразность приме­нения в школе основных приемов укрупнения дидактических единиц (совместное изучение взаимосвязанных вопросов, состав­ление обратных задач, деформированные упражнения)».

Укрупненной дидактической единицей Эрдниевы называют систему родственных единиц учебного материала, в которой симметрия, противопоставления, упорядоченные изменения компонентов учеб­ной информации в совокупности благоприятствуют возникнове­нию единой логико-пространственной структуры знания. Знание, которым учащиеся овладевают посредством методи­ческой системы УДЕ, обладает качеством системности.

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

1.   Аргинская И.И. Математика. 1 класс. Пособие для учителя к стабильному учебнику. – М.: Федеральный научно-методический центр им. Л.В. Занкова, 1996

2.   Аргинская И.И. Математика. 3 класс. - М.: Федеральный научно-методический центр им. Л.В. Занкова, 1997

3.   Аргинская И.И. Математика. Методич. пособие к уч.1-го кл. нач. шк. М.: Федеральный научно-методический центр им. Л.В. Занкова, 2000

4.   Бантова М.А., Бельтюкова Г.В. Методика преподавания математики в начальных классах. – М.: «Просвещение», 1984

5.   Волкова С.И. Карточки с математическими заданиями 4 кл. М.: «Просвещение», 1993

6.   Гейдман Б.П., Иванина Т.В., Мишарина И.Э.Математика 3 класс. – М.: Книжный дом «ЧеРо» изд. Московского университета, МЦНМО, 2000

7.   Гнеденко Б.В. Формирование мировоззрения учащихся в процессе обучения математике. – М.: «Просвещение», 1982. – 144 с.-(Библиотека учителя математики).

8.   Грин Р., Лаксон Д. Введение в мир числа. – М.: 1984

9.   Далингер В.А. Методика реализации внутрипредметных связей при обучении математике. – М.: «Просвещение», 1991

10.             Жиколкина Т.К. Математика. Книга для учителя. 2 кл. – М.: «Дрофа», 2000

11.             Журнал «Начальная школа» 1981-1998 гг.

12.             Зайцев В.В. Математика для младших школьников. Методическое пособие для учителей и родителей. –М.: «Владос», 1999

13.             Истомина Н.Б. Методика обучения математике в начальных классах. Уч.пособие. – М.: «ACADEMA»

14.             Лавриненко Т.А. Как научить детей решать задачи. – Саратов: «Лицей», 2000

15.             Леонтьев А.И. К вопросу о развитии арифметического мышления ребенка. В сб. «Школа 2100» вып.4 Приоритетные направлнеия развития образовательной программы – М.: «Баласс», 2000, с.109

16.             Математическое развитие дошкольников. Реценз. Бабаева Т.И. Уч.-метод. Пособие – С-Петербург: «Детство-Пресс», 2000

17.             Моршнева Л.Г., Альхова З.И. Дидактический материал по математике. – Саратов: «Лицей», 1999 г.

18.             Нешков Н.И., Чесноков А.С. Дидактический материал по математике для 4-го кл. – М.: «Просвещение», 1985

19.             Носова Е.А., Непомнящая Р.Л. Логика и математика для дошкольников. – С-П.: «Детство Пресс», 2000

20.             Петерсон Л.Г. Математика 1 класс. Методические рекомендации. – М.»БАЛАСС», «С-ИНФО», 2000

21.             Сергеев И.Н., Олехин С.Н., Гашков С.Б. Примени математику. – М.: «Наука», 1991

22.             Уткина Н.Г. Материалы к урокам математики в 1-3 кл. – М.: «Просвещение», 1984

23.             Эрдниев П.М., Эрдниев Б.П. Теория и методика обучения математике в начальной школе. – М.: «Педагогика», 1988. – 208 с.