Навигация
2. Преобразование Галилея
Пусть одно и то же явление описывается в двух инерциальных системах отсчета. Возникает вопрос о пересчете от описания явления в одной системе отсчета к описанию того же явления в другой системе. В качестве грубой иллюстрации можно представить себе две радиолокационные установки: одну – расположенную на земле, а другую – на самолете; вопрос состоит тогда в пересчете от показаний одной установки к показаниям другой.
Для такого пересчета нужно, прежде всего, знать связь между координатами и временем х, у, z, t в одной системе отсчета и координатами и временем х', у', z', t' в другой системе. Старая физика принимала как нечто самоочевидное существование единого мирового времени t, одинакового во всех системах отсчета. Поэтому с точки зрения старой физики необходимо было положить t' = t или, самое большее, допустить изменение начала отсчета времени.
Если рассматривать два события, происшедших в моменты времени t и π, то промежуток времени между ними должен был (с точки зрения старой физики) получиться одинаковым во всех системах отсчета. Отсюда,
t – π= t'-π' (1.01)
Далее, старая физика считала очевидным, что длина твердого стержня, измеряемая в двух системах отсчета, должна получаться одинаковой. (Вместо длины твердого стержня можно рассматривать расстояние между «одновременными» положениями двух точек, которые необязательно связаны жесткой связью.) Если обозначить координаты начала и конца стержня (или данных двух точек) в одной системе отсчета через (x, у, z) и (ξ, η, ζ) и в другой системе через (x', у', z') и (ξ', η', ζ '). то. согласно старой физике, должно быть
(x – ξ)2 + (y – η) 2 + (z – ζ) 2 = (x' – ξ')2 + (у' – η') 2 + (z' – ζ ')2 (1.02)
Из (1.01) и (1.02) однозначно вытекает общий вид преобразования, связывающего координаты и время х, у, z, t с координатами и временем х', у', z'. Это преобразование состоит из переноса начала отсчета координат и времени, из поворота пространственных координатных осей и из преобразования вида
![]()
x' = x – Vxt
y'=y-Vyt,
z' =z – Vzt,
t' = t, (1.03)
где Vxt, Vyt, Vzt – постоянные, физический смысл которых легко найти: это есть скорость движения штрихованной координатной системы относительно нештрихованной (точнее – составляющие этой скорости в нештрихованной системе). Преобразование (1.03) носит название преобразования Галилея.
Таким образом, старая физика утверждала, что если дана инерциальная система отсчета, то координаты и время во всякой другой системе отсчета движущейся относительно нее прямолинейно и равномерно, связаны с (х, у, z, t) преобразованиями Галилея (с точностью до переноса начала и поворота осей). Преобразование Галилея удовлетворяет принципу относительности в отношении законов механики, но не удовлетворяет ему в отношении законов распространения света.
Действительно, уравнение распространения фронта световой волны меняет в результате преобразования Галилея свой вид. Если бы преобразование Галилея было правильным (а принцип относительности в общей форме – неправильным), то существовала бы только одна инерциальная система в смысле нашего определения, и по измененному виду уравнения распространения фронта волны было бы возможно определить скорость движения (даже равномерного и прямолинейного) всякой другой системы отсчета относительно этой единственной инерциальной системы («неподвижного эфира»). Отрицательный результат многочисленных точнейших опытов, поставленных с целью обнаружения такого относительного движения, не оставляет сомнений в том, что форма закона распространения фронта волны одна и та же во всех неускоренных системах отсчета и что, следовательно, принцип относительности во всяком случае применим и к электромагнитным явлениям.
Отсюда следует, что преобразование Галилея в общем случае неправильно и должно быть заменено другим.
3. Преобразование Лоренца
Преобразование Лоренца показывает, как изменяются расширенные координаты события при переходе от одной инерциальной системы отсчета к другой инерциальной же системе. Пусть инерциальная система «Бета» движется относительно инерциальной системы «Альфа» с постоянной скоростью v, причем ось хβ скользит по оси х, а оси yβ, zβ всегда остаются соответственно параллельными осям yα, zα. Для конкретности будем предполагать, что система «Альфа» связана с ракетой «Альфа», а система «Бета» – с ракетой «Бета». Счет времени в обеих системах условимся вести от того момента, когда их начала координат совпали (иными словами, обе системы отсчета имеют одно и то же «начальное событие» О – прохождение ракеты «Альфа», мимо ракеты «Бета»).
Для упрощения формул единицы времени и длины выбираются таким образом, чтобы скорость света была равна единице и являлась величиной безразмерной. Для этого достаточно, например, выражать промежутки времени в секундах, а расстояния – в «световых секундах» (понимая под «световой секундой» отрезок, проходимый светом в течение одной секунды).
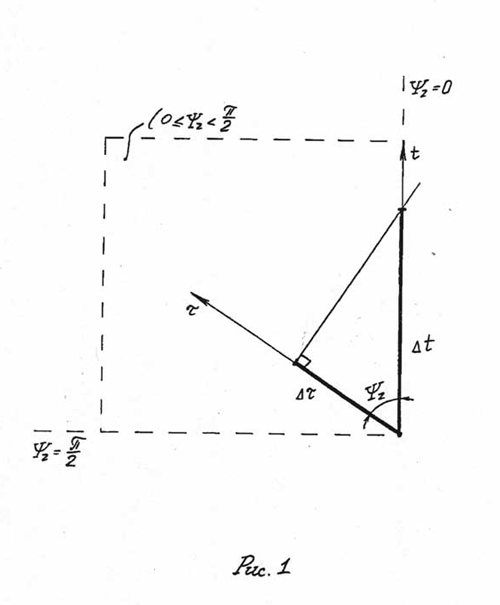
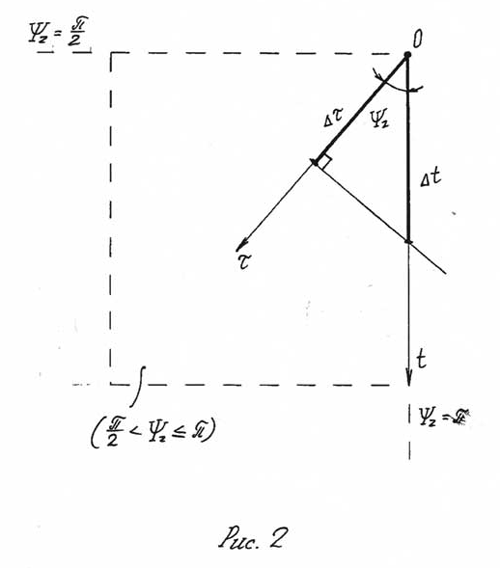
Некоторое событие S характеризуется в системе «Альфа» расширенными координатами xα, yα, zα, tα. Каковы его расширенные координаты xβ, yβ, zβ, tβ в системе «Бета»? Чтобы ответить на этот вопрос, обратимся к пространственно-временному графику, построенному в системе «Альфа» (рис. 2), предполагая, что рассматриваемое событие произошло на оси xα (а значит, и на оси хβ), так что yα= zα= yβ = zβ=0.
AS – это расстояние события S (точнее, того места, где оно произошло) от ракеты «Альфа», т.е. его пространственная координата хα.
АВ – это расстояние между ракетами в момент tα. Так как ракета «Альфа» удаляется от «Беты» со скоростью v, а в момент tα =0 они были рядом, расстояние AB = vtα.
BS = AS – AB= хα – vtα это расстояние события S от ракеты «Бета», как оценил бы его альфацентрист, которому могло бы даже казаться, что именно данная величина должна служить бетацентристу координатой хβ, события S в системе «Бета». Однако, как мы сейчас увидим, сам бетацентрист с такой оценкой не согласится; поэтому «спорную» величину BS = хα – vtα обозначим пока через x'. Отказ бетацентриста признать величину х' координатой хβ события S в системе «Бета» имеет два веских основания.
Во-первых, по мнению бетацентриста точка В пространственно-временного графика изображает положение ракеты «Бета» отнюдь не в момент события 5, а позже (раз речь идет о хβ координате, а не хα, одновременность следует понимать в смысле системы «Бета»!). С точки зрения бетацентриста, одновременное с событием S положение ракеты «Бета» соответствует точке С (прямая CS параллельна оси нулевого tβ).
Во-вторых, на этом пространственно-временном графике альфацентриста все расстояния измерены масштабом, покоящимся в системе «Альфа», тогда как при определении координаты хβ надо во всем поступать по правилам системы «Бета». С точки зрения бетацентриста, масштаб альфацентриста не находится в покое, а движется со скоростью v и потому может иметь неправильную длину.
Таким образом, поправки, которые внесет бетацентрист в оценку альфацентриста, сведутся к следующему:
1) к замене отрезка BS отрезком CS, параллельным оси хβ, что равносильно умножению величины х' на некоторый коэффициент k1, зависящий от угла φ=arc tg v, но одинаковый для всех событий.
2) к изменению единицы длины, что также равносильно умножению величины х' еще на один коэффициент k2, тоже зависящий только от v.
Учитывая обе поправки, мы можем написать:
хβ= k1 k2 х'= k1 k2(хα – vtα),
или, рассматривая произведение k1 k2 как новый коэффициент К (зависящий от v),
хβ= K(хα – vtα).
Полученная формула преобразования координаты х при переходе к другой инерциальной системе отсчета отличается от галилеевской только наличием коэффициента K.
На рис. 2 видно, что при переходе к новой системе отсчета меняется также и временная дата события: в системе «Альфа» событие S произошло в момент tα, а в системе «Бета» – в момент tβ.
Графически tα (временная дата события S в системе «Альфа») выражается отрезком MS, т.е. расстоянием точки S от оси нулевого tα.
Временная дата того же события tβ определяется по часам, покоящимся в системе «Бета». Пространственно – временная трасса этих часов изображается прямой RS, причем точка R соответствует прохождению стрелки этих часов через нуль (в системе «Бета» событие В считается одновременным с начальным событием О). Таким образом, временная дата tβ события S в системе «Бета» соответствует отрезку RS, однако не в том масштабе, в каком tα соответствует расстоянию MS. Ведь секунда по часам, покоящимся в системе «Бета», может существенно отличаться от секунды по часам, покоящимся в системе «Альфа», а каждый физик при измерениях должен полагаться только на часы, неподвижные относительно избранной им системы.
Поскольку единицы длины и времени выбираются не независимо, а с таким расчетом, чтобы скорость света численно равнялась единице (например, единица времени – секунда, а единица длины – световая секунда), они должны изменяться благодаря движению в одинаковое число раз (иначе был бы нарушен принцип постоянства скорости света). Следовательно, поправочный коэффициент k2, введенный ранее для длин, справедлив также и для отрезков времени.
Что же касается перехода от отрезка NS к отрезку RS, то он, в силу подобия треугольников NRS и BCS, тоже сводится к умножению на введенный уже коэффициент k1. Отрезок же MN равен vxα (как катет треугольника OMN, в котором tg φ = v). Поэтому
tβ= k2 ∙ RS = k2 ∙ k1NS= k1 k2 (MS – MN)= k1 k2(tα-vxα),
или окончательно
tβ= K (tα-vxα),
где K = k1 k2 – знакомый уже нам коэффициент, зависящий только от v (в принятой нами системе единиц t и х выражаются в секундах, a v – безразмерная величина).
Полученная формула преобразования временной даты события при замене одной инерциальной системы отсчета другой инерциальной же системой противопоставляется галилее-ньютоновскому представлению о единой для всех систем универсальной шкале времени. Эта формула отражает как зависимость хода часов от их движения, так и различие в понимании одновременности.
К полученным нами двум формулам преобразования расширенных координат события
хβ= K(хα – vtα),
tβ= K (tα-vxα)
могут быть еще добавлены очевидные соотношения
yβ= yα, zβ=zα,
которые показывают, что при переходе к другой системе, движущейся вдоль оси х, «поперечные» координаты у и z не изменяются.
Похожие работы
... и то же значение для всех наблюдателей – подвижных и неподвижных). Если Лоренц считал, что значение скорости света зависит от наблюдателя, то специальная теория относительности считает, что скорость света имеет одно и то же значение независимо от скорости наблюдателя. Противоречие отрицания эфира-вакуума. Согласно первому положению наша Земля – это и физическое тело, и объект Бытия. Вместе с ...
... Эйнштейн интерпретировал преобразования Лоренца кинетически, т.е. как характеризующие свойства движения в пространстве и времени, тем самым заложив основы теории относительности. Он снял проблему эфира, упразднив его, радикально изменил классические представления о пространстве и времени. Явления, описываемые теорией относительности, называются релятивистскими (от латинского - относительный) и ...
... 11. П.Ф. Фильчаков. Справочник по высшей математике, М., Наука, с. 645. *** Сегодня, со всей ясностью становится очевидным, что открытый А.Эйнштейном процесс замедления Времени описанный в специальной и общей теориях относительности требует более глубокой проработки и осмысления. Необходимо разобраться и понять внутреннюю работу механизма замедления Времени, а не только знать причины вследствие, ...
... луч искривился. Для Эйнштейна это означало, что в реальном мире лучи света искривляются, когда проходят на достаточно малом расстоянии от массивного тела. Общая теория относительности Эйнштейна заменила ньютоновскую теорию гравитационного притяжения тел пространственно-временным математическим описанием того, как массивные тела влияют на характеристики пространства вокруг себя. Согласно этой ...

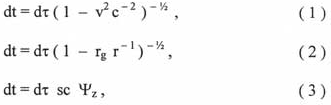
0 комментариев