Навигация
Математические и алгоритмические основы решения задачи
16288
знаков
2
таблицы
8
изображений
2. Математические и алгоритмические основы решения задачи
Для того чтобы приступить к построению и анализу математической модели игры, необходимо определить вероятности обнаружения кораблей при различном их расположении и различных системах поиска
На поле из n клеток расположен одноклеточный корабль. Определим вероятность попадания в корабль k-ым выстрелом, то есть его уничтожение.
В качестве пространства элементарных исходов выбора игрока В рассмотрим множество стратегий обстрела игрового поля, каждая стратегия состоит из n выстрелов,
,
где 
– номер выбранной клетки, то есть рассмотрим множество всех выборок из n по n клеток. Очевидно, что это пространство содержит 
элементов и все эти стратегии равновозможны. Количество стратегий с благоприятным исходом, то есть количество выборок, содержащих на k-ом месте искомую клетку
.
Вероятность попадания
.
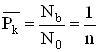Определим вероятность уничтожения корабля за k выстрелов. Это событие состоит в том, что корабль может быть уничтожен либо первым выстрелом, либо вторым и т.д., то есть благоприятная выборка из k клеток содержит искомую клетку с кораблем. Количество благоприятных стратегий определится как число неупорядоченных выборок из множества n – 1 клеток по k – 1 (одна клетка, занятая кораблем не учитывается при выборке), умноженное на число перестановок в самой выборке k! и число перестановок клеток оставшихся за выборкой (n – k)!:)!. Вероятность попадания в одноклеточный корабль за k выстрелов
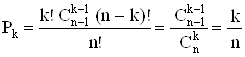. (1)
Усложним задачу. На поле из n клеток расположен двухклеточный корабль. Определим вероятность первого попадания в корабль (в одну из его клеток) выстрелом с номером k. Полное число всевозможных стратегий, как и в предыдущем случае, равно 
, а число благоприятных стратегий определяется как сумма благоприятных стратегий попадания в одну клетку и попадания во вторую клетку, то есть . Вероятность попадания k-ым выстрелом равна 
.
Очевидно, что при обстреле m-клеточного корабля или m одноклеточных кораблей, вероятность попадания k-ым выстрелом равна
.
Определение вероятности попадания в двухклеточный корабль за k выстрелов, сведется к определению количества стратегий, содержащих искомые клетки в первых k выстрелах. Число таких стратегий будет вычисляться как следующая сумма
,
где 
– выборки, содержащие либо первую клетку, либо вторую клетку, 
– выборки, содержащие одновременно две клетки. Следовательно
и после преобразований получим
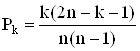. (2)
Заметим, что аналогичным образом можно определить вероятность попадания за k выстрелов в корабль из m клеток. Задача попадания за k выстрелов в многоклеточный корабль хотя бы один раз является задачей поиска корабля. Очевидно, что если учесть геометрию корабля, то можно предложить систему его поиска, при которой вероятность обнаружения становится выше. Действительно, при поиске двухклеточного корабля можно рассмотреть подмножество всех стратегий, содержащих обстрел, например, клеток только с четными или с нечетными номерами. Поиск двухклеточного корабля сведется к поиску одноклеточного корабля на этом подмножестве. Полагая n четным, для оптимальной вероятности попадания за k выстрелов получим
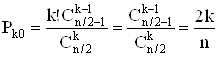. (3)
Найденное значение вероятности больше вероятности, полученной выше
,
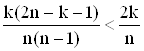при всех значениях 
.
Оптимальная стратегия поиска трехклеточного и четырехклеточного корабля может быть получена аналогичным образом.
Вероятность попадания в игре «Морской бой»
Всего клеток 100
а) вероятность попасть в какой-нибудь корабль равна 
;
б) вероятность попасть в четырехпалубный равна 
;
в) вероятность попасть в однопалубный равна ;
Всего кораблей 10, не однопалубных 6, «клеточек» 16.
а) вероятность попасть в четырехпалубный равна 
;
б) вероятность попасть в трехпалубный равна 
;
в) вероятность попасть в двухпалубный равна .
Похожие работы
... до expression2. В том случае, когда значение expression1 оказывается больше значения expression2, тело цикла не будет выполнятся вовсе. 2. РАЗРАБОТКА ПРОГРАММЫ 2.1 Постановка задачи Составить программу для игры в «Морской бой» игрока с компьютером. Программа должна позволять расставлять корабли на поле 10 х 10, контролировать правильность их расстановки, давать противникам возможность ...
... помещен. С компонентом связывается объект класса TStatusPanel, который определяет панели компонента. Этот компонент находится на странице Палитры компонентов Win32. 2. РАЗРАБОТКА ПРОГРАММЫ 2.1. Постановка задачи Разработать игровую программу «Морской бой», которая включает игровую панель, состоящую из двух полей для человека и компьютера. На поле расставляются 10 кораблей разного класса. Четыре ...
... Нет col_dec = 1 col_ship = col_ship + 1 Рис. 6. Функция Disposition или Generation Тестирование Чтобы проверить корректность работы программы нужно провести тестирование. Бой с противником продолжается до полной победы, т.е. пока не будут уничтожены все 10 кораблей одного из противников. Если первым свои корабли потерял компьютер, игроку выводится сообщение о победе Рис. 7. ...
... дипломной работе. Нами был проведен эксперимент в начальной школе ОАО «Газпром» и в Православной гимназии города Москвы, целью, которого являлось выявление влияния информационных технологий на отношение к миру у детей младшего школьного возраста с различным мировосприятием. 6.В первой части эксперимента в качестве прототипа было выбрано исследование, проведенное в США, Японии, Мексике Центром ...
0 комментариев