КОНСТРУКТОРСКАЯ ЧАСТЬ

2. КОНСТРУКТОРСКАЯ ЧАСТЬ

 

2.1 Общий принцип работы программы

 

При загрузке программы создаётся матрица размерностью 10 на 10 с помощью циклов с параметрами. В этой матрице любая координата соответствует идентичной координате клетки игрового поля. Далее все операции производятся с данной матрицей, а рисование происходит в методе Form1_Paint по данным значениям матрицы.

for (int i = 0; i < 10; i++)

{

for (int j = 0; j < 10; j++)

{

matr[i, j] = 0;

}

}

В методе Form1_Paint мы рисуем все графические объекты, используемые в программе: клетка, нолик и крестик

 

private void Form1_Paint(object sender, PaintEventArgs e)

{

e.Graphics.DrawLine(pen3, k * 30 + 2, i * 30 + 2, k * 30 + 28, i * 30 + 28);

e.Graphics.DrawLine(pen3, k * 30 + 28, i * 30 + 2, k * 30 + 2, i * 30 + 28);

e.Graphics.DrawRectangle(pen1, 30 * k, 30 * i, 30, 30);

}

Следующий метод заключается в том, что генерирует случайную величину, т.е. с помощю него компьютер ставит нолик в произвольном порядке

 

private int get_random(int min, int max)

{

int r = 0;

r = rnd.Next(min, max);

return r;

}

Обновление всего игрового поля происходит в методе restart():

public void restart()

{

for (int i = 0; i < 10; i++)

{

for (int j = 0; j < 10; j++)

{

matr[i, j] = 0;

}

}

2.2 Принцип игры человек против человека

По событию формы Click запускается метод Form1_Click.

private void Form1_Click(object sender, EventArgs e)

{

}

Здесь производится проверка на попадание курсора мыши в область клетки. Для игры против человека необходимо отметить RadioButton human. В этом случае производится проверка булевой переменной access. Access отвечает за переход хода к другому игроку. Если access равен true, то значение соответствующей matr[k, i] становится равным единице и в методе Form1_Paint рисуется крестик в соответствующей клетке. Если же access равен false, то matr[k, i] становится равным двум и рисуется нолик. После каждого хода запускается метод proverka. Он проверяет на совпадение поставленную клетку и рядом стоящие. Если таковые имеются то запускается метод proverka2 и он работает до тех пор, пока не найдёт 5 одинаково заполненных подряд идущих клеток.

Определение координат положения мыши происходит следующим образом. Если в момент нажатия кнопки мыши указатель находится в пределах одной из клеток, то при нажатии кнопки ноль, элемент матрицы matr[i,j] меняется на единицу, соответственно в клетке ставится крестик, при следующем нажатии кнопки - ставится нолик,и так поочереди:

if (access == true)

{

matr[k, i] = 1;

access = false;

proverka(k, i);

}

else

matr[k, i] = 2;

access = true;

proverka(k, i);

}

После каждого хода запускается вышеупомянутый метод proverka(k, i),в котором использованы операторы ветвления if-else и который находит 2 подряд идущих крестика(нолика), идущих в любом направлении. В этом случае параметр, отвечающий за количество подряд идущих крестиков (ноликов) line увеличивается в методе proverka2. Цикл продолжается до тех пор, пока линия не будет состоять из пяти крестиков(ноликов). Далее следует сообщение, которое повествует, какой игрок выиграл и вопрос: «Хотите сыграть еще раз?». В данной программе для этого используется следующий метод:

MessageBox.Show("Хотите сыграть еще раз?", "выиграли крестики", MessageBoxButtons.YesNo);

При нажатии кнопки «Да» игровое поле обновляется с помощью метода restart(), при нажатии «Нет» приложение закрывается.

2.3 Принцип игры компьютера

При игре с компьютером, когда выполняется условие computer.Checked мы используем другой подход:

if (matr[k, i] == 0)

{

matr[k, i] = 1;

access4 = true;

_x = k; _y = i;

proverka(k, i);

AI();

}

После хода пользователя осуществляется метод AI(), в котором использован алгоритм нахождения двух подряд идущих крестиков. Второй крестик ищется в восьми клетках вокруг первого. Если таковых нет, то компьютер ставит нолик в любом месте относительно клетки с крестиком с помощью метода random_AI(). Если методом AI было найдено два подряд идущих крестика, то метод AI2 (int z, int q, int c, int d) ищет три подряд идущих крестикаи на продолжении той же прямой (это осуществляется с помощью фомальных параметров c и d) и ставит нолик на той же линии то чтобы предотвратить появление четырёх крестиков. Если три подряд идущих крестика не найдено, то также срабатывает метод random_AI(). Компьютер не может походить дважды, так как после каждого хода закрывается доступ к другому методу с помощью переменных access3 и access4. Все ходы компьютера происходят в зависимости от того, куда был поставлен последний крестик, то есть компьютер занимает оборонительную позицию.

После каждого пользовательского хода или хода компьютера также осуществляется проверка всего поля на наличие пяти идущих подряд крестиков (ноликов) с помощью вышеописанного метода proverka(). Так же можно продолжить игру с компьютером после недоигранной партии с человеком, просто нажав соответствующию RadioButton computer и наоборот.

3. ТЕХНОЛОГИЧЕСКАЯ ЧАСТЬ

 

3.1 Правила игры

Правила игры состоят в том, что необходимо выстроить линию из пяти крестиков (ноликов) в любом направлении и каким угодно способом (по горизонтали, вертикали или диагонали). Соответственно ваш противник должен выстроить подобную линию быстрее вас или не давать вам построить такую линию. Игра начинается с того, что в любом месте игрового поля ставится крестик , ваш противник ставит нолик , и так до тех пор пока не будет выстроена линия. В данной программе чтобы выиграть, необходимо первым составить линию.

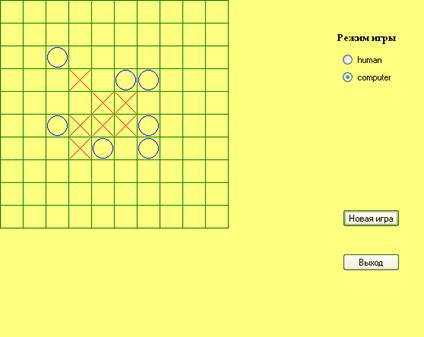
Рис.1. Игровое поле

3.2 Интерфейс программы

Программа предоставляет возможность играть в игру крестики-нолики. Для запуска программы сделайте двойной щелчок по ярлыку программы. На экране появится основное окно программы, имеющее следующий вид (рис. 1):

На окне размещено игровое поле и две кнопки – Новая игра и Выход, а также кнопки выбора режима игры: пользователь против пользователя(human) и пользователь против компьютера(computer). Для начала новой игры необходимо нажать кнопку Новая игра, а потом уже играть в соответствии с правилами игры. Для выхода из программы нужно нажать кнопку Выход.

При победе одного из игроков появляется сообщение (рис. 2) «Хотите сыграть еще раз?». Если нажать кнопку «Да», то соответственно начнется новая игра, а если «Нет», то программа закрывается.

Рис.2. Сообщение

ЗАКЛЮЧЕНИЕ

В процессе выполнения курсовой работы были изучены новые возможности языка высшего уровня C#. В том числе была изучена графическая подсистема Visual Studio. В процессе создания приложения был реализован алгоритм, который в дальнейшем возможно усовершенствовать. Все поставленные задачи были выполнены и разработка популярной игры «Крестики-нолики» прошла успешно.

СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ

1. Чарльз Петцольд. Программирование для Microsoft WINDOWS на С#. Издательско-торговый дом “Русская Редакция”, Москва 2002 - 576 с.

2. Разработка Windows-приложений на Microsoft Visual Basic .NET и Microsoft Visual C# -NET. Учебный курс MCAD/MCSD/Пер. с англ. — М.:

Издательско-торговый дом «Русская Редакция», 2003. — 512 стр.: ил.

3. MSDN 2005