Информатика и компьютерная техника

Министерство образования и науки Украины

Харьковский национальный университет

им. В.Н. Каразина

Методические рекомендации по курсу "Информатика и компьютерная техника"

Составители: Епишев Сергей Николаевич

Иванов Валентин Васильевич

Чуркина Людмила Георгиевна

Введение

Методические указания по курсу “Информатика и компьютерная техника”. Выпуск I. Основы ЭВМ /Состав. С.Н. Епишев, Ю.Г. Гузненков, Л.Г. Чуркина –Харьков: ХНУ, 2005. –7хх с.

Методические указания предназначены для ознакомления студентов с курсом “Информатика и компьютерная техника”. В них рассматриваются вопросы, связанные с преобразованием информации, методами ее обработки и хранения с помощью компьютерных технологий. В цифровых вычислительных машинах информация представляется в виде наборов двоичных кодов. Существует много способов кодирования числовой информации. Некоторые из них основываются на переводе чисел из десятичной системы счисления в двоичную. Перевод чисел из десятичной системы счисления в двоичную и наоборот рассматривается в данных указаниях довольно подробно. Современные компьютеры обладают мощным программным обеспечением, позволяющим решать различные задачи. В методических указаниях приводится классификация средств программного обеспечения и назначение его отдельных групп. Большое внимание уделено вопросам алгоритмизации задач решаемых на ЭВМ, поскольку даже при наличии хорошего программного обеспечения, иногда приходится составлять программы при решении некоторых задач. Для закрепления материала курса, в конце каждого параграфа приведены контрольные вопросы.

Рекомендовано кафедрой экономической кибернетики и прикладной экономики экономического факультета Харьковского национального университета им. В.Н. Каразина для студентов экономических специальностей всех форм обучения.

Понятие информатики. Источники и предпосылки информатики

 

Становление информатики как научной дисциплины относится к 60-годам нашего столетия. В самом общем смысле под информатикой понимают фундаментальную естественную науку, изучающую процессы передачи, накопления и обработки информации.

Термин «Informatique» был введен французами на рубеже 60-70-х годов. Но еще раньше американцами был введен в употребление термин «Computer Science» для обозначения науки о преобразовании информации, базирующийся на вычислительной технике. В настоящее время термины «Informatique» и «Computer Science» употребляются в эквивалентном смысле.

В нашей стране для обозначения новой научной дисциплины применялись термины «вычислительные науки» или «вычислительное дело», использование же термина «информатика» сдерживалось употреблением его в области, связанной с документалистикой. Начиная с 60-х годов, название информатика в нашей стране получила иная научная дисциплина – теория научной информации и научно-информационной деятельности. И хотя для обозначения этой отрасли знания в русском языке предлагались и другие термины (вначале «теория научной информации», затем «документалистика»), очень скоро абсолютно доминирующим стал термин информатика. Этому во многом способствовал выход фундаментального труда ведущих специалистов в данной области – А.И. Михайлова, А.И. Черного и Р.С. Гиляревского – под названием «Основы информатики». Новое толкование этого термина относится к 1976 году, когда появился русский перевод книги Ф. Бауэра и Г. Гооза «Введение в информатику». Волну широкого интереса к информатике вызвал выход летом 1982 года монографии академика В.М. Глушкова «Основы безбумажной информатики». Окончательное утверждение термина «информатика» связанно с созданием в марте 1983 года Отделения информатики, вычислительной техники и автоматизации Академии Наук.

В качестве источников информатики обычно называют две науки: документалистику и кибернетику.

Документалистика сформировалась в конце XIX века в связи с бурным развитием производственных отношений. Ее расцвет пришелся на 20-30 –е годы XXв., а основным предметом стало изучение рациональных средств и методов повышения эффективности документооборота.

Основы близкой к информатике технической науки кибернетики были заложены трудами по математической логике американского математика Норберта Винера, опубликованными в 1948 г., а само название происходит от греческого слова kyberneticos – искусный в управлении.

Впервые термин кибернетика ввел французский физик Андре Мари Ампер в первой половине XIX в. Он занимался разработкой единой системы классификации всех наук и обозначил этим термином гипотетическую науку об управлении, которой в то время не существовало, но которая, по его мнению, должна существовать.

Сегодня предметом кибернетики являются принципы построения и функционирования систем автоматического управлении, а основными задачами – методы моделирования процессов принятия решений, связь между психологией человека и математической логикой, связь между информационным процессом отдельного индивидуума и информационными процессами в обществе, разработка принципов и методов искусственного интеллекта. На практике кибернетика во многих случаях опирается на те же программные и аппаратные средства вычислительной техники, что и информатика, а информатика, в свою очередь, заимствует у кибернетики математическую и логическую базу для развития этих средств.

Предмет и задачи информатики

 

Что же это за наука, или даже более того – область человеческой деятельности – информатика?

Приведем определение информатики, данное Международным конгрессом в Японии в 1978 г.: «Понятие информатики охватывает области, связанные с разработкой, созданием, использованием и материально-техническим обслуживанием систем обработки информации, включая машины, оборудование, математическое обеспечение, организационные аспекты, а также комплекс промышленного, коммерческого, административного, социального и политического воздействия».[1]

Известно определение информатики данное академиком А.П. Ершовым: «…фундаментальная естественная наука, изучающая процессы передачи и обработки информации»[2].

В.С. Михалевич в работе «Информатика – новая область науки и практики» дает следующее определение: «Информатика – комплексная научная и инженерная дисциплина, изучающая все аспекты разработки, проектирования, создания, оценки, функционирования машинизированных (основанных на ЭВМ) систем переработки информации, их применения и воздействия на различные области социальной практики».

Современные учебники информатики определяют ее предмет следующим образом.

«Информатика, самостоятельная научная дисциплина, предметом которой стали свойства информации, ее поведение в техногенных, социальных и биологических системах, а также методы и технологии, ориентированные на сбор, обработку, хранение, передачу и распространение информации, или, кратко, информационной технологии».[3]

Приведена формулировка предмета информатики не единственная. Популярным является определение согласно которому, «Информатика – это наука об описании, представлении, интерпретации, формализации и применении знаний, накопленных с помощью вычислительной техники, с целью получения новых знаний».

Приведем еще несколько определений фигурирующих в наших отечественных украинских учебниках.

«Информатика – наука, которая изучает информационные процессы, методы и средства получения, преобразования, передачи, хранения и использования информации, применения информационных технологий».[4]

«Інформатика – комплексная научная и инженерная дисциплина, которая изучает все аспекты проектирования, создания, оценивания, функционирования компьютерных систем обработки информации, их применения и влияния на различные отрасли социальной практики».[5]

Следуя Симоновичу С.В. («Информатика для экономистов и юристов», СПб: Питер, 2004. -688с.) будем считать, что «Информатика – это техническая наука, систематизирующая приемы создания, обработки и передачи данных средствами вычислительной техники, а также принципы функционирования этих средств и методы управления ими.

В настоящее время информатика выходит за рамки узкой технической дисциплины, относящейся к средствам вычислительной техники и информационным технологиям. Отныне ее предмет становится шире. Информатика в XXI веке становится естественной наукой, занимающей положение между другими естественными, техническими и общественными науками. Ее предмет составляют информационные процессы, протекающие в природе, обществе и технических системах. Ее методы в своем большинстве основаны на взаимодействии программных и аппаратных средств вычислительной техники с другими техническими системами, с человеком и обществом. Ее цель – научное обоснование эффективных приемов создания, распределения и потребления всех трех типов информационных ресурсов и методологическое обеспечение разработки новых информационных систем. Ее центральная роль заключается в представлении своего аппарата и понятийной базы другим естественным, общественным и техническим дисциплинам».

Информатика и информационные технологии

 

До появления электронной вычислительной техники были известны две информационные технологии: рукописная и книгопечатание. Технология как строго научное понятие означает определенный комплекс научных и инженерных знаний, воплощенных в способах, приемах труда, наборах материально-вещественных факторов производства, способов их соединения для создания какого-то продукта или услуги. В таком понимании термин технология неразрывно связан с машинизацией того или иного производственного или социального процесса. Появление компьютеров, их использование для обработки информации и решения разнообразных задач привело к появлению нового научного направления – «компьютерной информатики» и новой «электронной информационной технологии», связанной с автоматизированной обработкой информации.

«Информационная технология в своем полном виде должна отвечать следующим требованиям:

1.         Высокая степень расчленения процесса на стадии (фазы), что открывает новые возможности для рационализации всего процесса и перевода его на машинную технику. Это – важнейшая характеристика технологического процесса, возникающего на базе машин.

2.         Системная полнота (целостность) процесса, который должен включать весь набор элементов, обеспечивающих необходимую завершенность действий человека в достижении поставленной цели. Требуется также определенная пропорциональность в соотношении различных звеньев технологической цепи и в уровне их развития. Опыт показывает, в частности, что как ни улучшай отдельные элементы информационно-перерабатывающего процесса на базе электронно-вычислительных машин, это не дает целостной технологии и не дает, следовательно, требуемого эффекта.

3.         Регулярность процесса и однозначность его фаз, позволяющие применить средние величины при характеристике этих фаз и, следовательно, их стандартизацию и унификацию. В результате появляется возможность учета, планирования, диспетчеризации информационных процессов. В такой развитой форме, имеющей все отмеченные признаки, информационно-коммуникационные процессы выступают на высокой исторической стадии развития – в машинизированных кибернетических системах».[6]

Доступность персональных компьютеров, ориентированных на людей, не имеющих специального образования в области информатики и навыков работы с компьютером, вызвали повышенный интерес к компьютерной информатике представителей разных профессий. Диапазон эффективного применения компьютеров для автоматизированной обработки информации постоянно возрастает.

«Информатика как самостоятельная наука вступает в свои права тогда, когда для изучаемого фрагмента мира построена так называемая информационная модель. И хотя общие методологические принципы построения информационных моделей могут быть предметом информатики, само построение и обоснование информационной модели является задачей частной науки. Понятия информационной и математической моделей очень близки друг к другу, поскольку и та и другая являются знаковыми системами. Информационная модель – это сопряжение, через которое информатика вступает в отношение с частными науками, не сливаясь с ними и в то же время не вбирая их в себя».[7]

«Отсюда уже следует состав информатики – это три неразрывно и существенно связанные части: технические средства, программные и алгоритмические … Важно не забывать, что без алгоритмов предмета информатики не существует».[8]

Проблемы компьютерной информатики сводятся к разработке:

–     информационной модели задачи;

–     алгоритма обработки информации;

–     программы, реализующей алгоритм на языке компьютера.

Таким образом, структура системы компьютерной информатики базируется на триаде: модель – алгоритм – программа.

Теоретической основой компьютерной информации является методология решения задач с помощью компьютера.

Решение задач обработки информации связано с выполнением различных операций над информацией, обеспечивающих получение требуемого результата. Для автоматизации этого процесса необходимо прежде всего формализовать условие задачи и разработать методы поиска решения, в результате чего полученную формализованную информационную модель задачи и алгоритм поиска ее решения можно программно реализовать на компьютере.

Качество решения задач с использованием компьютеров определяется теми алгоритмами обработки информации, которые в них закладываются человеком. Компьютеры выполняют роль инструмента, с помощью которого реализуются эти алгоритмы.

Поэтому общая методология решения задач с помощью компьютера связана с разработкой эффективных методов формализации задачи, алгоритмов их решения.

Контрольные вопросы

 

1.   Дайте определение понятия «информатика».

2.   Чем вызван повышенный интерес к компьютерной информатике?

3.   Какова структура системы компьютерной информатики?

4.   В чем суть электронной информационной технологии решения задач?

5.   Что является теоретической основой компьютерной информатики?

6.   Что понимается под информационной моделью задачи?

7.   Какова роль человека и компьютера в процессе решения задачи?

Информация и ее структура

«Кто владеет информацией, тот владеет миром» – знаменитый афоризм, принадлежащий «отцу» кибернетики Норберту Виннеру. Слово «информация» переводится на русский язык как сведения.

В последние годы оно стало употребляться в различных сферах и при этом приобрело многозначное толкование.

В энциклопедическом словаре приводится следующее ее определение: информация – это новые сведения об окружающем мире, получаемые в процессе взаимодействия с ним.

С точки зрения кибернетики под информацией следует понимать только те сведения, которые нужны пользователю и полезны ему. Можно сказать, что информация неотделима от процесса информирования человека. Сведения становятся информативными только тогда, если они новы, достоверны, и уменьшают неопределенность по интересующему вопросу (объекту).

С точки зрения науки информатики «информация» – это предмет обработки, то есть предмет труда.

Поэтому мы будем исходить из того, что информация – это сведения об условиях задачи и методах ее решения, зафиксированные на том или ином носителе информации (бумаге, диске и т.п.).

Одна из разновидностей информации – экономическая, возникающая в процессе производственно-хозяйственной деятельности объекта, отображающая явления экономической жизни общества и используемая для управления этой деятельностью.

Чтобы более точно определить место информации в различных понятиях, связанных с ней, дадим следующие три определения:

Данные – любые сведения о ком-либо или о чем-либо;

Информация – любые новые, полезные для пользователя, сведения;

Знания – структурированные данные, способные вызывать машинные программы для выполнения операций над своими элементами и обозначать другую информацию и ее структурные элементы. В знаниях содержатся сведения о порядке обработки данных, что позволяет автоматизировать процесс их обработки.

Для удобства обработки информационных совокупностей информацию (данные) структурируют, то есть выделяют различные конструкции, имеющие экономический смысл. Наиболее простым структурным элементом информации является реквизит.

Реквизит – сочетание букв, цифр и символов, имеющих смысловое содержание и не поддающееся дальнейшему делению, не теряя при этом смысла. Каждый реквизит имеет форму и содержание.

Форма – это наименование реквизита (строки или графы документа), а содержание – его значение. Одному наименованию реквизита может соответствовать множество его значений.

Реквизиты по своему назначению подразделяются на два вида: реквизиты-признаки и реквизиты-основания. Признаки характеризуют качественную сторону (объекта), хозяйственной операции, т.п., а основания – количественную (цена, количество, сумма и т.п.).

Реквизиты неоднородны по характеру выполняемых над ними действий: в процессе обработки над основаниями выполняются арифметические действия или логические типа сравнения (=, > и т.п.), над признаками – логические (поиск, выборка, группировка).

Реквизиты, объединяясь, образуют составные единицы информации (СЕИ) более высокого уровня.

Показатель – информационная совокупность с минимальным составом реквизитов, достаточным для образования документа. Каждому показателю соответствует одно основание и относящиеся к нему признаки:

П→ (Р₁, Р₂ …, Р_n, Q), где

Q – основание; Р₁, Р₂,…, Р_n – признаки.

Основным средством отображения экономической информации является документ.

Документ – составная структурная единица информации, состоящая из нескольких показателей, структура и значение которых удостоверено ответственным лицом.

Как правило, в документе показатели связаны некоторыми логическими отношениями. В документе столько показателей, сколько оснований.

На основании однотипных документов формируются информационные массивы, хотя сам документ также может содержать массивы показателей, а показатели – массивы значений реквизитов.

Совокупность информационных массивов и программ по их ведению, обработке, хранению и т.п. образуют базы данных.

Таким образом, структура информации – это конкретные информационные образования (единицы), наделенные экономическим смыслом.

Иерархический принцип выделения информационных образований (единиц) позволяет при использовании компьютерной техники эффективно перейти к машинным структурам информации.

Пример 1.

Дана форма документа «Накладная», содержащая информацию о поступлении товарно-материальных ценностей от поставщиков на склад предприятия (организации).

Организация Р1 Предприятие	Шифр
	грузополучателя	постав- щика		склада (секция)	вида операции
	Р2	Р3	Р4		Р5

 

 Р₇ » Р₈ 20_{_}Р₉_года

 

Накладная № Р₆

Отправитель Р₁₀

Получатель  Р₁₁

Основание Р₁₂

 

Номер прейскуранта ему	Шифр товара, тары	Наименование товарно-материальных ценностей	Единица намерения	Сорт	Количество (вес)		Цена	Сумма
					Брутто	Нетто
Р13	Р14	Р15	Р16	Р17	Q1	Q2	Q3	Q4

Отпустил Разрешил

Получил _________________________

Требуется:

1)         определить в документе количество реквизитов, в том числе: признаков (Р) и оснований (Q);

2)         установить количество показателей К(П);

3)         перечислить операции, выполняемые над реквизитами-признаками и основаниями.

Порядок выполнения задания:

1) в приведенной форме документа всего 21 реквизит и 3 подписи заверяющие документ и подтверждающие правомерность оформляемой хозяйственной операции – поступления товарно-материальных ценностей от поставщика на склад предприятия или организации. В документе 3 реквизита являются сложными (составными). Так, реквизиты Р₂:Р₅ составляют реквизит «шифр», реквизиты Р₇:Р₉ – «дату», а Основания Q₁ и Q₂ –«количество» (вес). Реквизитов-признаков в «Накладной» насчитывается 17, а оснований – 4. Признаки характеризуют место свершения хозяйственной операции (отправитель, получатель, их шифры), время (дата) и качественную характеристику товарно-материальных ценностей (номер прейскуранта, шифр и наименование товара, единица измерения, сорт). Основания дают информацию о величине поставок товарно-материальных ценностей в количественном (натуральном) и стоимостном выражении (сумме), об их цене.

2) В документе столько показателей, сколько оснований, то есть 4: количество (брутто, нетто), цена, сумма (К(П)=4). Например, показателю цена товара соответствует (Р₁₃, Р₁₄, Р₁₅, Р₁₆, Р₁₇,Q₃).

3) Операции, выполняемые над реквизитами и признаками:

3а) над реквизитами-признаками выполняются следующие логические операции. Документированный массив информации целесообразно группировать по шифрам поставщика, склада, вида операции и шифру товара с целью составления различных ответов о движении товарно-материальных ценностей;

3б) над основаниями в документе выполняются арифметические операции. Так, по каждой строке документа производится операция таксировка:

В целом по документу «Накладная» определяется также итог по графе

«Сумма» путем суммирования данных по указанной графе:

где: n – количество заполненных строк в документе (i=1,n).

Итоги могут быть получены и по группировочным признакам (поставщику, складу, шифру товара), если это необходимо для учетного и аналитического процессов.

Контрольные вопросы

 

1.   Дайте определение понятий «информация» и «экономическая информация».

2.   Что понимается под структурой экономической информации?

3.   Дайте определение информационных единиц: реквизита, документа.

4.   Чем отличается реквизит-признак от реквизита-основания?

5.   Дайте определение составных единиц информации: показателя массива.

6.   Какие основные операции выполняются над признаками и основаниями при обработке экономической информации?

7.   Взять любую форму первичного документа по какому-либо участку работ и выполнить анализ структуры документа, как это сделано в примере.

Системы счисления

 

Под системой счисления понимают совокупность приемов наименования и обозначения (записи) чисел. Условные знаки, применяемые для обозначения чисел называют цифрами. Кроме цифр применяются также разделители (+,- ,^, , ^. и т.п.). Как и обычный язык, язык чисел имеет свой алфавит. Общепринятым языком чисел стала десятичная система счисления. Любое число в ней представляется с помощью набора из десяти цифр: 0,1,2,3,4,5,6,7,8,9. Причем, значение каждой цифры в записи числа зависит от позиции, которую она занимает в числе. Так, например, в записи 555,5 цифра 5 встречается четыре раза, но в каждой позиции она имеет разный смысл: крайняя левая цифра 5 означает количество сотен и имеет значение 500, следующая цифра 5 означает количество десятков, 5, стоящая перед запятой, означает количество единиц и, наконец, цифра 5 после запятой – количество десятых долей единицы. Десятичная система счисления является позиционной.

Позиционная система счисления – это система, у которой при записи чисел одна и та же цифра имеет различные значения в зависимости от позиции, которую она занимает в числе. В любой позиционной системе счисления используется определенное количество различных цифр (символов) для обозначения чисел. Поэтому они различаются своим базисом и основанием.

Базис системы счисления – набор различных цифр, применяемых для написания чисел в данной системе. Количество цифр в базисе называется основанием системы счисления.

Позиционные системы счисления именуются соответственно своему основанию: десятичная – основание 10, восьмеричная – основание 8, двоичная – основание 2. Могут быть системы счисления, использующие более 10 цифр. Например, в шестнадцатеричной системе счисления применяются шестнадцать цифр.

Широкое распространение десятичной системы счисления, по-видимому, связано с физиологическим строением рук (ног) человека (10 пальцев на руках (ногах)). Была бы у нас дюжина (12) пальцев на руках, то, скорее всего мы бы пользовались двенадцатиричной системой.

Поскольку за основание позиционной системы счисления можно взять любое целое положительное число большее единицы, то таких систем можно создать очень много.

Для оценки пригодности той или иной системы счисления в качестве основы для конструирования вычислительной машины имеет значение, кроме простоты осуществления арифметических операций в ней, также и то, что обычно называют экономичностью системы. Под этим понимается тот запас чисел, которые можно записать в данной системе с помощью определенного количества знаков. Чтобы в десятичной системе счисления записать 1000 чисел (от 1 до 999), необходимо 30 знаков (по 10 цифр для каждого разряда). А в двоичной системе можно с помощью 30 знаков записать 2¹⁵ различных чисел (так как для каждого двоичного разряда нужны только цифры 0 и 1, то с помощью 30 цифр мы можем записать числа, содержащие до 15 двоичных разрядов). Но 2¹⁵>1000, поэтому, имея 15 различных разрядов, можно записать больше различных чисел, чем с помощью трех десятичных разрядов. В общем случае, если взять n знаков, а за основание системы счисления принять некоторое число x, то получится n/x разрядов, и количество чисел которые при этом можно записать, будет равно x^n/x. Рассмотрим это выражение как функцию переменной x. Максимум этой функции достигается при x =2,718281828459045…. Это число есть основанием натуральных логарифмов. Но оно не является целым. Ближайшими целыми к этому числу будут 3 и 2. В силу простоты технической реализации имитирования цифр двоичной системы (0,1) в ЭВМ наиболее часто используется двоичная система счисления, хотя известны реализации ЭВМ с троичной системой счисления, например «Сетунь» созданная в МГУ.

Чтобы определить, в какой системе счисления записано число, ее основание записывают в скобках внизу после числа. Например, 708₍₁₀₎, 36₍₈₎, 101₍₂₎.

В любой позиционной системе счисления ее основание записывается как 10, то есть единица в старшем разряде и 0 в младшем.

Все позиционные системы счисления строятся по одному общему принципу: выбирается некоторое целое положительное число Р>1 - основание системы счисления; запись любого числа М представляется в виде полинома, т.е. комбинации степеней основания системы счисления Р с коэффициентами а₀, а₁, а₂, …, а_k, принимающими значения от 0 до Р-1, т.е. из базиса системы:

 

М_(р) = а_k×р^k+ а_k-1· р^k-1+...+ а_{0 ·} р⁰+ а_-1·р^-1+...+ а_-m·р^-m…

Если при записи числа опустить степени основания системы счисления, то число можно записать в следующем компактном виде:

 

M_(р)= а_kа_k-1...а₁, а₀ а_-1 ... a_-m…

Компактность представления чисел, а также удобные алгоритмы выполнения операций сложения, умножения, обусловили широкое распространение позиционных систем счисления.

Непозиционные системы счисления построены иначе. Например, в системе римских цифр имеется набор символов: единица I, пять V, десять X, пятьдесят L и т.д., комбинация которых позволяет представить любое число. Так, число 77 в этой системе счисления запишется так: LXXVII. В этой системе значение каждого символа не зависит от того места, на котором он стоит. В приведенной записи числа 77 цифра X используется 2 раза, и каждый раз обозначает одну и ту же величину – десять единиц.

Один из первых создателей электронных вычислительных машин профессор Атанасов А. предложил использовать в ЭВМ двоичную систему счисления. Набор символом, используемых для представления и обработки информации в компьютере минимален. Он включает всего два символа – 0 и 1, с помощью комбинации которых (последовательностей единиц и нулей) можно записать любое число, причем при этом может потребоваться различное число бит (двоичных разрядов), что и указано в таблице 1. Использование в современных ЭВМ двоичного представления информации, как было отмечено выше, объясняется удобством технической реализации устройств хранения и обработки информации.

Таблица 1. - Изображение чисел в позиционных системах счисления, применяемых в компьютерах

Десятичное Р=10	Двоичное Р=2	Восьмеричное Р=8	Шестнадцатеричное Р=16
1	2	3	4
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15	0 1 10 11 100 101 110 111 1000 1001 1010 1011 1100 1101 1110 1111	0 1 2 3 4 5 6 7 10 11 12 13 14 15 16 17	0 1 2 3 4 5 6 7 8 9 А В С D E F
16	10000	20	10

Перевод чисел из одной системы счисления в другую

 

При решении задач на ЭВМ исходные данные обычно задаются в десятичной системе счисления; в этой же системе, как правило, нужно получить и результат решения задачи. Но если ЭВМ работает в какой-либо другой системе счисления, например в двоичной, то возникает необходимость перевода чисел из одной системы счисления в другую. При рассмотрении правил такого перевода мы ограничимся только такими системами счисления, у которых базисными числами являются последовательные целые числа от 0 до P-1 включительно, где P – основание системы счисления.

При переводе числа из десятичной системы счисления в систему счисления с основанием Р перевод целой и дробной части числа производится отдельно. Перевод целого числа из десятичной системы счисления в любую другую с основанием Р производится многократным делением десятичного числа на основание Р, пока частное не станет меньше Р. Последнее частное будет старшим разрядом числа, а остаток от первого деления на Р – младшим. На практике удобно пользоваться следующей схемой, которую проиллюстрируем при переводе числа 56 из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную:

56₍₁₀₎→ ₍₂₎ → ₍₈₎ → ₍₁₆₎

56	2
56	28	2
0	28	14	2
	0	14	7	2
		0	6	3	2
			1	2	1 последнее частное
				1

Ответ: 56₍₁₀₎=111000₍₂₎;

56	8
56	7
0

Ответ: 56₍₁₀₎=70₍₈₎.

56	16
48	3
8

Ответ: 56₍₁₀₎=38₍₁₆₎.

 

Чтобы перевести правильную дробь из десятичной системы счисления в любую другую с основанием P, ее последовательно умножают на P, при этом каждый раз умножается только дробная часть образовавшегося произведения. Процесс перевода продолжается либо до достижения заданной точности, либо до обнаружения периода. Дробь в системе счисления с основанием P записывается в виде дроби из целых частей образовавшихся произведений, начиная с первого.

Перевод десятичных дробей удобно производить по схеме, которую проиллюстрируем на примерах.

Перевести:

1)   0,75₍₁₀₎→₍₈₎

0,	75 8
6,	00

Ответ: 0,75₍₁₀₎=0,6₍₈₎

2) 0,7₍₁₀₎→₍₁₆)

0,	7 16
11,	2
	16
3,	2

Ответ: 0,7₍₁₀₎=0,В(3)₍₁₆₎

2) 0,4₍₁₀₎→₍₂₎

0,	4 2
0,	8 2
1,	6

Ответ: 0,4₍₁₀₎=0,01₍₂₎

Примеры для отработки навыков

1) 0,45₍₁₀₎→₍₂₎;2) 0,6₍₁₀₎ →₍₈₎;3) 0,95₍₁₀₎ →₍₁₆₎;

4) 425,6₍₁₀₎ →₍₈₎;5) 147,4₍₁₀₎ →₍₂₎;6) 5827,8₍₁₀₎ →_(16).

Перевод числа, записанного в системе счисления P, в десятичную систему выполняется с учетом веса каждого разряда или путем записи числа в виде разложения по степеням основания P. Например,

1)   1101₍₂₎ →₍₁₀₎

1101₍₂₎=1· 10³ + 1· 10² + 0·10¹+ 1· 10⁰ ₍₂₎ →1·8+1·4+0·2+1₍₁₀₎=13₍₁₀₎;

или по схеме:

двоичное число 1 1 0 1₍₂₎десятичное число

8 4 2 1

1х1=1

0х2=0

1х4=4

1х8=8

Ответ: 13₍₁₀₎

Во втором случае перевод выполняется с учетом веса каждого разряда.

2)   354,4₍₈₎ =3·8²+5·8¹+4·8⁰+4·8^-1₍₁₀₎ =192+40+4+0,5₍₁₀₎=236,5₍₁₀₎;

3)   A1F,8₍₁₆₎=A·16²+1·16¹+F·16⁰+8·16^-1₍₁₆₎ = 10·16²+1·16+15+8/16₍₁₀₎= =2591,5₍₁₀₎.

Примеры для отработки навыков.

1) 1А0,Е₍₁₆₎ → ₍₁₀₎;2) –1011101,101₍₂₎ → ₍₁₀₎;  3) 101,1₍₈₎ → ₍₁₀₎

 

Переход из двоичной в восьмеричную и шестнадцатеричную системы счисления и обратно

Поскольку основание восьмеричной системы 8=2³, то разложение числа по степеням 8 легко переводится в разложение по степеням 2 и наоборот. При этом каждая цифра восьмеричной системы (0,…,7) имеет свое разложение по степеням 2. Например,

2₍₈₎=0·2²+1·2¹+0·2⁰=(010)₂  6₍₈₎=1·2²+1·2¹+0·2⁰=(110)₂

Тогда переход от восьмеричного представления числа в двоично-восьмеричное осуществляется путем замены каждой восьмеричной цифры соответствующей двоичной триадой.

720₍₈₎=7·8²+2·8¹+0·8⁰=(1·2²+1·2+1·2⁰)2⁶+(0·2²+1·2+0·2⁰)·2³+(0·2²+0·2¹+0·2⁰)=1·2⁸+1·2⁷+1·2⁶+0·2⁵+1·2⁴+0·2³+0·2²+0·2¹+0·2⁰=111010000₍₂₎=11 010 000₍₂₎.

7  2 0

Для представления двоичного числа в восьмеричной системе надо число разбить на двоичные триады влево и вправо от запятой и затем заменить каждую триаду, соответствующей ей восьмеричной цифрой.

101 111 011, 001 100₍₂₎ = 573,14₍₈₎

Четыре двоичных разряда позволяют закодировать любую десятичную цифру и получить 16 различных кодовых комбинаций, из которых 10 (от 0000 до 1001) используются для представления десятичных цифр. Кодовые комбинации, соответствующие числам 10 и более, условно обозначаются первыми буквами латинского алфавита (графа 4 таблицы 1). Так получается шестнадцатеричная система счисления. В программах для ЭВМ, чтобы не выписывать длинную вереницу нулей и единиц, вместо каждых четырех разрядов (тетрад) записывается их шестнадцатеричный эквивалент. Например, шестнадцатеричный эквивалент числа 0101 0001 1111 0011 будет 51F3.

 

Арифметические операции в электронных вычислительных машинах

В вычислительных машинах вся информация представляется в двоичной форме, а для выполнения вычислений используется непосредственно двоичная система счисления.

Арифметические операции с двоичными числами производятся так же, как с десятичными, с той лишь разницей, что в десятичной системе цифры каждого разряда возрастают в порядке 1,2,…,8,9, а при достижении величины 10 в этом разряде записывается 0 и делается перенос единицы в старший разряд. В двоичной системе используются только два символа 0 и 1, поэтому цифры в каждом разряде могут изменяться только в пределах этих двух значений, после этого происходит перенос в более старший разряд.

Таблица 1. -Таблица сложения двух бинарных чисел, имеет следующий вид:

Здесь 10 – это 2 в двоичной системе счисления.

Например:

1110,01₍₂₎10111,011₍₂₎

+ 1010,10₍₂₎ + 11101,101₍₂₎

11000,11₍₂₎ 110101,000₍₂₎

Обычно для представления положительных и отрицательных чисел используются величины со знаками, причем при представлении положительных чисел знак «+» можно опускать, а знак «–» при изображении отрицательных чисел должен ставиться, что для реализации на вычислительных машинах неудобно. В вычислительных машинах используется форма представления чисел в дополнительных кодах, а знаки «+» и «–» используются для указания арифметических операций.

В двоичной системе счисления числа могут быть представлены в форме дополнения до основания системы счисления, то есть до 2. В двоичном дополнительном коде всем положительным числам предшествует 0, а отрицательным числам – единица. Таким образом, при представлении чисел в дополнительном коде крайний левый бит (старший) является знаковым: 0 означает положительное число, а 1 – отрицательное.

 1011 1100 101  110 111 000 001 010 011 0100 0101

-5  -4 -3 -2 -1  0  1 2 3 4 5

Числа, стоящие по разные стороны от нуля, являются взаимно дополнительными, то есть их сумма всегда равна 0. Чтобы представить двоичное число в дополнительной форме, его инвертируют (заменяют 0 на 1, а 1 – на 0) прибавляют к нему 1. Операция вычитания выполняется путем сложения дополнительных кодов.

Пример:

Выполнить вычитание 10111,1–1010,1.

На первом этапе необходимо указанные числа выровнять по значности (они должны иметь одинаковое количество разрядов) и представить в дополнительном коде.

[10111,1]доп.= 0 10111,1

[ –01010,1]доп.= 1 10101,0 + 00000,1 = 1 10101,1.

На втором этапе выполняется вычитание как сложение с дополнительным числом, то есть:

0 10111,1

+ 1 10101,1

0          01101,0 = 1101.

Операции умножения, деления, возведения в степень и вычисления функций процессор не выполняет, их необходимо выполнять программным путем, используя сдвиги влево и вправо. Сдвиг двоичного числа на одну позицию влево приводит к его удвоению подобно тому, так сдвиг десятичного числа на одну позицию вправо – к его уменьшению на 10. Сдвиг двоичного числа на одну позицию вправо делит его пополам.

Контрольные вопросы и примеры

1.   Что понимается под системой счисления?

2.   Чем отличается позиционная система счисления от непозиционной?

3.   Дайте определение базиса и основания позиционной системы счисления.

4.   Как перевести число из 10→ 2, из 10→ 16?

5.   Как перевести число из 2→ 10, из 8→10, из 16→10?

6.   Каков принцип построения позиционных систем счисления?

7.   Как изображаются числа в дополнительном коде?

8.   Опишите схему вычитания чисел с помощью дополнительного кода.

9.   Перевести числа из одной системы счисления в другую:

а) 625₍₁₀₎→₍₂₎;б) 3628,5₍₁₀₎ →₍₁₆₎;в) 1024,4₍₁₀₎ → ₍₈₎;

г) 134,6₍₈₎ →₍₁₀₎;д) –ВСО₍₁₆₎ →₍₁₀₎.

10. Записать числа в дополнительном коде:

а) 1563,04₍₁₀₎  г) –3А01₍₁₆₎

б) –2,149₍₁₀₎д) –01010,101₍₂₎

в) –0,1001101₍₂₎е) –37,54₍₈₎

11. Выполните арифметические операции в двоичной системе:

а) 1011,11б)1011,101

 + 101,11  - 110,11

12. Комплексное задание: в таблице 2 приведены по вариантам числа в десятичной, двоичной и восьмеричной системах счисления:

Таблица 2.Системы счисления

№ варианте	Десятичная система	Двоичная система	Восьмеричная система
1	2	3	4
1	107.99	1100101.100100	152.01
2	357.94	1000111.011111	204.31
3	273.66	1111001.001110	110.44
4	845.76	1111010.100101	243.25
5	214.38	1110010.010101	743.56
6	584.16	1010101.100111	676.43
7	343.37	1101100.010011	114.53
8	128.69	1110101.000111	631.04
9	513.76	1010111.111001	204.33
10	778.47	1111001.010111	301.75

Выполнить:

1)   перевести число из 10-ой системы счисления в двоичную, восьмеричную и шестнадцатеричную;

2)   перевести число из 2-ой системы счисления в десятичную и восьмеричную;

3)   перевести число из восьмеричной системы счисления в десятичную и двоичную системы;

4)   выполнить сложение чисел, находящихся в 2 и 4 графах таблицы 2, пользуясь двоичной арифметикой;

5)   выполнить вычитание двоичных чисел, находящихся в тех же графах таблицы 2.

 

Основы математической логики

 

В математических и других рассуждениях постоянно встречаются повествовательные предложения, образованные путем видоизменения некоторого предложения с помощью слова не или связывания предложений с помощью слов и, или, если …, то (или влечет), тогда и только тогда, когда. Эти пять слов или комбинаций слов называются сентенциональными связками. Они являются основой для построения сложных предложений (т.е. таких повествовательных предложений в которых содержится одна или более чем одна связка), составленных их простых предложений (т.е. таких, каждое из которых или не содержит связку, или рассматривается как «неразложимое»).

Повествовательное предложение о котором можно сказать истинно оно или ложно мы будем называть высказыванием. Множество повествовательных предложений и сентенциональных связок образует исчисление высказываний. Если обозначать высказывания большими латинскими буквами и ввести для сентенциональных связок условные обозначения (значки), то можно перейти к логическим формулам результатом которых будут логические значения – истина или ложь.

Дадим определения для основных логических операций.

1. Конъюнкцией (или операцией логического умножения) двух высказываний A и B называют высказывание C, которое истинно тогда и только тогда, когда истины оба высказывания входящие в конъюнкцию. Конъюнкция (иногда логическое «и») обозначается значком  и записывается так: AB.

2. Дизъюнкцией (или операцией логического сложения) двух высказываний A и B называют высказывание C, которое ложно тогда и только тогда, когда ложны оба высказывания входящие в дизъюнкцию. Дизъюнкция (иногда логическое «или») обозначается значком Ú и записывается так: AÚB.

3. Отрицанием высказывания A называют высказывание B которое ложно тогда и только тогда когда истинно исходное высказывание A, обозначают  (иногда ØA).

4. Импликация высказываний (или условное предложение) обозначается AÞB и задается с помощью следующей таблицы, называемой таблицей истинности для импликации:

A	B	AÞB
Истина	Истина	Истина
Истина	Ложь	Ложь
Ложь	Истина	Истина
Ложь	Ложь	Истина

4.    Эквиваленция или эквивалентность двух высказываний обозначается AÛB и задается следующей таблицей истинности:

A	B	AÛB
Истина	Истина	Истина
Истина	Ложь	Ложь
Ложь	Истина	Ложь
Ложь	Ложь	Истина

Среди всех сложных высказываний или логических формул наибольший интерес представляют такие, которые принимают значение истина при любых истинностных значениях входящих в них логических переменных (высказываний). Они называются тождественно истинными высказываниями или тавтологиями, обозначаются значком . Для доказательства общезначимости логических формул (того, что формула есть тавтология) пользуются таблицами истинности или применяют основные законы эквивалентности математической логики, которые также доказываются применением таблиц истинности.

 

Законы эквивалентности

 

1.         Законы коммутативности (они позволяют переставлять операнды Ù,Ú и Û):

(AÙB)Û(BÙA)

(AÚB)Û(BÚA)

(AÛB)Û(BÛA)

2. Законы ассоциативности (они позволяют нам пренебрегать скобками):

(AÙB) ÙС Û A Ù(BÙC)

(AÚB) ÚС Û A Ú(BÚC)

3.         Законы дистрибутивности (они позволяют раскрывать скобки):

 

AÚ(B ÙС) Û (A ÚB)Ù(AÚC)

AÙ(B ÚС) Û (A ÙB)Ú(AÙC)

4.         Законы де Моргана:

Ø(AÙB) Û ØAÚØB

Ø(AÚB) Û ØAÙØB

 

5.         Закон отрицания: Ø(ØA) Û A

6.         Закон исключенного третьего: AÚØA Û истина

7.         Закон противоречия: AÙØA Û ложь

8.         Закон импликации: (AÞB)Û( ØAÚB)

9.         Закон равенства: (AÛB) Û (AÞB)Ù(BÞA)

10.       Законы упрощения Ú:

AÚA Û A

AÚИстина ÛИстина

AÚЛожьÛА

АÚ(АÙВ)ÛА.

11. Законы упрощения Ù:

АÙАÛА

АÙИстинаÛА

АÙЛожьÛЛожь

АÙ(АÚВ)ÛА

12. Закон тождества:

АÛА.

Операции математической логики имеют свое старшинство, т.е. порядок их выполнения: 1) Ø, 2) Ù, 3) Ú, 4) Þ, 5) Û.

Пример 1. Доказать общезначимость формулы:

(АÛВ)Ù(ВÛС)Þ(АÛС)

Для доказательства воспользуемся таблицей истинности. Заметим, что количество строк в такой таблице равно 8 (2ⁿ – где, n – количество логических переменных).

Будем в таблице истину обозначать – и, а ложь – л.

А	В	С	АÛВ	ВÛС	(АÛВ)Ù(ВÛС)	АÛС	Вся формула
и	и	и	и	и	и	и	и
и	и	л	и	л	л	л	и
и	л	и	л	л	л	и	и
л	и	и	л	и	л	л	и
и	л	л	л	и	л	л	и
л	и	л	л	л	л	и	и
л	л	и	и	л	л	л	и
л	л	л	и	и	и	и	и

Пример 2. Используя основные законы эквивалентности доказать эквивалентность формул U и V, когда

U = XÞ(XÙY)Þ((XÞY)ÞY)ÞZ

V = YÞ(XÞZ)

Применяя основные законы эквивалентности к каждой формуле в отдельности покажем, что они дают одно и то же логическое выражение (формулу). Далее, на основании равенства правых частей сделаем заключение о равенстве левых.

Рассмотрим V:

V = YÞ(XÞZ)

ØYÚ(ØXÚZ)

ØYÚØXÚZ

Рассмотрим U:

U = XÞ(XÙY)Þ((XÞY)ÞY)ÞZ

ØXÚ(ØXÚØYÚ((Ø(ØXÚØY)ÚY)ÙZ))

ØXÚØXÚØYÚ(((XÙØY)ÚY)ÙZ)

ØXÚØYÚ(((XÚY)Ù(ØYÚY)ÙZ)

ØXÚØYÚ((XÚY)Ù Z)

ØXÚØYÚ((XÙZ)Ú(YÙZ))

ØXÚØYÚ(XÙZ)Ú(YÙZ)

(ØXÚ(XÙZ))Ú(ØYÚ(YÙZ))

((ØXÚX)Ù(ØXÚZ))Ú((ØYÚY)Ù(ØYÚZ))

(ØXÚZ)Ú(ØYÚZ)

ØXÚZÚØYÚZ

ØXÚØYÚZ

Тем самым эквивалентность доказана.

Пример 3. Записать логическое выражение принимающее значение истина в случае когда точка с координатами (x,y) находится внутри заштрихованной области. На рисунке даны окружность с единичным радиусом и парабола у=х².

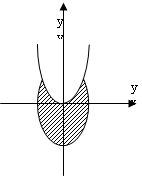
Рис.1. - Окружность с единичным радиусом

Выражение имеет следующий вид: (X²+Y²£1)Ù(Y£X²).

Пример 4. Записать логическое выражение, принимающее значение истина в случае когда точка с координатами (x,y) находится внутри заштрихованной области. На рисунке даны окружность с единичным радиусом и парабола у=х².

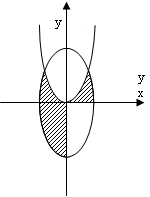
Рис.2. - Окружность с единичным радиусом

Выражение имеет следующий вид:

((X£0)Ù(X²+Y²£1)Ù(Y£X²))Ú((X²+Y²£1)Ù(Y£X²)Ù(Y³0)).

Контрольные вопросы

 

1.         Что такое сентенциональные связки?

2.         Дайте определение высказывания.

3.         Как определяются основные логические операции?

4.         Что значит общезначимость логической формулы?

5.         Выпишите основные законы эквивалентности.

6.         Какие приоритеты имеют логические операции?

7.         Пользуясь основными законами эквивалентности доказать общезначимость формулы:

(AÞB)Þ((BÞC)Þ(AÞC)).

Используя таблицу истинности доказать следующий закон эквивалентности:

(AÞB)Û( ØAÚB).