Навигация
АНАЛИЗ ТЕХНИЧЕСКИХ РЕШЕНИЙ
2. АНАЛИЗ ТЕХНИЧЕСКИХ РЕШЕНИЙ
2.1 Библиотека MFC
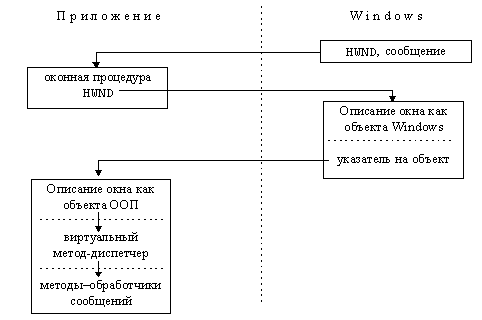
Система Microsoft Windows была разработана до того времени, когда идея объектно-ориентированного программирования нашла свое отражение в языке C++. Приложения на языке С реализовывались с применением функций программного интерфейса, называемых иногда функциями API (Application Programming Interface). Однако идеи объектно-ориентированного программирования требуют и наличия средств, позволяющих, с одной стороны, программировать в терминах классов, а с другой – сохранить возможность использования в приложениях функций API. Именно такой объектно-ориентированный интерфейс для Windows обеспечивает библиотека классов MFC (Microsoft Foundation Classes), входящая в состав пакета Visual C++.
Эта библиотека классов позволяет:
а) значительно сократить усилия по написанию программного кода приложений Windows;
б) уменьшить размер программного кода;
в) обрабатывать сообщения непосредственно методами класса без программирования цикла обработки сообщений;
г) выполнять непосредственный вызов любой функции Windows С;
д) легко преобразовывать Си-приложения в приложения на языке C++;
е) использовать все функции Windows API;
ж) легче адаптировать приложения к различным платформам, использовать как статически, так и динамически подключаемые библиотеки MFC;
з) значительно упростить применение таких возможностей, как элементы управления OLE, работа с базами данных, средства печати, управление наборами инструментария;
и) более эффективно использовать объектную ориентированность языка C++.

Рисунок 2.1 – Иерархия классов в библиотеке MFC
Следует отметить, что MFC инкапсулирует функции API в форме C++. Эта библиотека классов позволяет работать в терминах различных элементов Windows, таких, как окна, диалоги, элементы управления, а также в терминах графического интерфейса: контекст устройства, кисть и перо. Библиотека MFC создана как иерархический набор классов, позволяющих реализовывать Windows-приложения различных типов: диалоги, приложения с SDI или MDI интерфейсом, приложения, поддерживающие работу с базами данных, OLE-приложения. Базовым классом большинства классов библиотеки является класс CObject. В этом классе инкапсулированы общие методы работы с объектами: использование дампа объектов класса при отладке приложения, доступ к информации о классе объекта времени выполнения, сохранение и восстановление объектов класса. Большую часть библиотеки составляют классы, наследуемые от CObject и реализующие архитектуру приложения (рисунок 2.1)[1]: CWinThread, CWinApp, CDoc-Template, CDocument, CFrameWnd, CView и др.
2.2 Нечеткая логика ‑ математические основы
Нечеткое множество ‑ это пара (A, m), где A ‑ имя нечеткого множества, например: БОЛЬШОЙ, МОЛОДОЙ, ОТРИЦАТЕЛЬНО МАЛЫЙ, а m ‑ функция m:X-->L, называемая функцией принадлежности и обозначаемая обычно греческой буквой m. Часто полагается L = [0,1], а в качестве X используется некоторое множество вещественных чисел. m(x) интерпретируется как степень принадлежности элемента x из X нечеткому множеству A.
Характеристикой нечеткого множества выступает функция принадлежности (Membership Function)[4]. Обозначим через MFc(x) – степень принадлежности к нечеткому множеству C, представляющей собой обобщение понятия характеристической функции обычного множества. Тогда нечетким множеством С называется множество упорядоченных пар вида C={MFc(x)/x}, MFc(x) [0,1]. Значение MFc(x)=0 означает отсутствие принадлежности к множеству, 1 – полную принадлежность.
Проиллюстрируем это на простом примере. Формализуем неточное определение 'горячий чай'. В качестве x (область рассуждений) будет выступать шкала температуры в градусах Цельсия. Очевидно, что она будет изменяется от 0 до 100 градусов. Нечеткое множество для понятия 'горячий чай' может выглядеть следующим образом:
C={0/0; 0/10; 0/20; 0,15/30; 0,30/40; 0,60/50; 0,80/60; 0,90/70; 1/80; 1/90; 1/100}.
Так, чай с температурой 60 С принадлежит к множеству 'Горячий' со степенью принадлежности 0,80. Для одного человека чай при температуре 60 С может оказаться горячим, для другого – не слишком горячим. Именно в этом и проявляется нечеткость задания соответствующего множества.
Для нечетких множеств, как и для обычных, определены основные логические операции[5]. Самыми основными, необходимыми для расчетов, являются пересечение и объединение.
Пересечение двух нечетких множеств (нечеткое "И"): AÈB: MFAB(x)=min(MFA(x), MFB(x)).
Объединение двух нечетких множеств (нечеткое "ИЛИ"): AÇB: MFAB(x)=max(MFA(x), MFB(x)).
В теории нечетких множеств разработан общий подход к выполнению операторов пересечения, объединения и дополнения, реализованный в так называемых треугольных нормах и конормах. Приведенные выше реализации операций пересечения и объединения – наиболее распространенные случаи t-нормы и t-конормы.
Для описания нечетких множеств вводятся понятия нечеткой и лингвистической переменных.[4]
Нечеткая переменная описывается набором (N,X,A), где N – это название переменной, X – универсальное множество (область рассуждений), A – нечеткое множество на X.
Значениями лингвистической переменной могут быть нечеткие переменные, т.е. лингвистическая переменная находится на более высоком уровне, чем нечеткая переменная. Каждая лингвистическая переменная состоит из:
- названия;
- множества своих значений, которое также называется базовым терм-множеством T. Элементы базового терм-множества представляют собой названия нечетких переменных;
- универсального множества X;
- синтаксического правила G, по которому генерируются новые термы с применением слов естественного или формального языка;
- семантического правила P, которое каждому значению лингвистической переменной ставит в соответствие нечеткое подмножество множества X.
Рассмотрим такое нечеткое понятие как 'Цена акции'. Это и есть название лингвистической переменной. Сформируем для нее базовое терм-множество, которое будет состоять из трех нечетких переменных: 'Низкая', 'Умеренная', 'Высокая' и зададим область рассуждений в виде X=[100;200] (единиц). Последнее, что осталось сделать – построить функции принадлежности для каждого лингвистического терма из базового терм-множества T.
Существует свыше десятка типовых форм кривых для задания функций принадлежности.[2] Наибольшее распространение получили: треугольная, трапецеидальная и гауссовская функции принадлежности.
Треугольная функция (рисунок 2.2) принадлежности определяется тройкой чисел (a,b,c), и ее значение в точке x вычисляется согласно выражению:
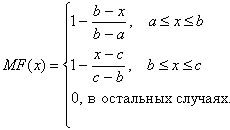 (2.1)
(2.1)
При (b-a)=(c-b) имеем случай симметричной треугольной функции принадлежности, которая может быть однозначно задана двумя параметрами из тройки (a,b,c).
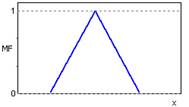
Рисунок 2.2 – Треугольная функция принадлежности
Аналогично для задания трапецеидальной функции (рисунок 2.3) принадлежности необходима четверка чисел (a,b,c,d):
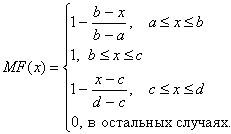 (2.2)
(2.2)
При (b-a)=(d-c) трапецеидальная функция принадлежности принимает симметричный вид.
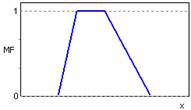
Рисунок 2.3 – Трапециидальная функция принадлежности
Функция принадлежности гауссова типа(рисунок 2.4) описывается формулой
![]() (2.3)
(2.3)
и оперирует двумя параметрами. Параметр c обозначает центр нечеткого множества, а параметр s отвечает за крутизну функции.
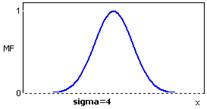
Рисунок 2.4 – Гауссовская функция принадлежности
Расширенная функция принадлежности гауссова типа(рисунок 2.5) описывается формулой
 (2.4)
(2.4)
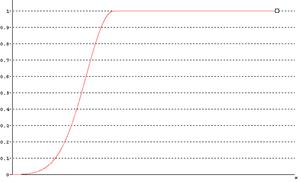
Рисунок 2.5 – Расширенная гауссовская функция принадлежности
Сигмоидальная функция принадлежности (рисунок 2.6) описывается формулой
![]() (2.5)
(2.5)
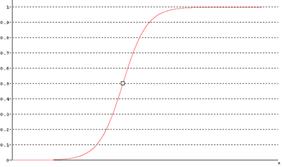
Рисунок 2.6 – Сигмоидальная функция принадлежности
Похожие работы
... в Win32 позволила реализовать так называемые многопотоковые приложения (multithread application). При этом выделяют два новых понятия — процесс (proccess) и поток (thread). Процессы в Win32 API примерно эквивалентны приложениям в Windows API. Для каждого процесса выделяются определенные системные ресурсы — адресное пространство, приоритеты и права доступа к разделяемым ресурсам и прочее, но не ...
... DriveType2.cpp. СОВЕТ Если вы хотите, чтобы эта программа полноценно работала в WinNT, следует также перехватить функцию GetDriveTypeW. Ещё одна реализация данного метода описана в статье «Перехват API-функций в Windows NT/2000/XP», автор Тихомиров В. А., публиковалась в RSDN Magazine #1 (будьте осторожны, там та же ошибка, что и у Джеффри Рихтера). ПРИМЕЧАНИЕ У этого метода есть ещё ...
... и PCCard32 (CardBus) PCMCIA. 6. Включены следующие подсистемы: DCOM, ActiveMovie v2.0 и DirectX v5.0. 7. Некоторые утилиты Windows 98 улучшены по сравнению с Windows 95. Операционная система MS Windows NT Windows NT имеет Windows-подобный графический интерфейс пользователя и предоставляет Win32 API — 32-разрядный интерфейс прикладного программирования для разработки ...
... предприятия. Для дальнейшего развития Системы необходимо рассчитать экономическую эффективность проекта. Для этого необходимо выбрать направление распространения Системы. Заказчиком системы выступало закрытое акционерное общество "Белгородский бройлер". Произведем расчет экономической эффективности проекта с точки зрения заказного проекта. Структура экономической части при создании программного ...


0 комментариев