Навигация
Проверка синтаксиса функциональной модели и вывод динамической модели
1. Проверка синтаксиса функциональной модели и вывод динамической модели.
Динамическая модель строится на основании функциональной модели и синтезируется пакетом Design/IDEF автоматически во время проверки синтаксиса функциональной модели. Для того, чтобы проверка стала возможной, необходимо разрешить эмуляцию CPN-моделей. Это делается путем установки метки CPN в окне Edit-Set Options-Methodology-Simulations. После установки метки в строке меню главного окна появляется новое меню CPN.
Для проверки синтаксиса необходимо вызвать команду "Check CPN Syntax" в данном меню и в появившемся окне указать параметры проверки. По окончании проверки появляется окно с отчетом, где указываются ошибки (если есть), а на функциональной модели появляются элементы сети Петри.
2. Краткие теоретические сведения о сетях Петри.
Сети Петри являются мощным инструментом исследования моделируемых систем благодаря их возможности описания многих классов дискретных, асинхронных, параллельных, распределенных, недетерминированных систем, благодаря наглядности представления их работы, развитому математическому и программному аппарату анализа.
Она представляет собой разновидность ориентированного графа, включающего в себя вершины двух типов: позиции и переходы. Позиции символизируют состояния и обозначаются как pi, а переходы обозначают собой действия (переходы из одного состояния в другое) и обозначаются как tj. Позиции и переходы соединены направленными дугами fk, каждая из которых имеет свой вес wk. Дуги также можно разделить на два типа: дуги, направленные от позиции к переходам, (p-t) и дуги, направленные от переходов к позициям (t-p). Исходя из этого, сеть Петри может быть формально представлена как совокупность множеств:
N = (P, T, F, W),
где P = {p1, p2… pn} - множество всех позиций (n - количество позиций),
T = {t1, t2… tm} - множество переходов (m - количество переходов),
F = (Fp-t, Ft-p) - множество дуг сети:
Fp-t = (pґt), Ft-p = (tґp) - множества дуг, ведущих соответственно от переходов к по-зициям и от позиций к переходам.
W = {w1, w2… wk} - множество весов дуг (k - количество дуг).
Каждая позиция может быть маркирована, т.е. содержать некоторое число фишек. Если обозначить числа фишек, находящихся в i-й позиции pi, как mi, то маркировка всей сети: M = {m1, m2… mn}. Тогда полное определение сети Петри, включая данные о началь-ной маркировке, можно записать в виде:
PN = (N, M0), где М0 - начальная маркировка сети.
3. Отладка динамической модели.
Если в результате проверки синтаксиса функциональной модели были обнаружены ошибки, то их список будет выведен в окне отчета. В процессе устранения ошибок удобно переходить от одной ошибки к другой с помощью команды "Next Reference"/"Previous Ref-erence" меню Select. Все ошибки показываются выделением.
4. Надписывание позиций.
Для надписывания какой-либо позиции сети Петри необходимо сначала создать метку (команда Create Label), затем ее выделить и вызвать команду "Place Name" меню CPN. После этого достаточно указать надписываемый объект.
5. Надписывание переходов.
Роль переходов сети Петри играют функциональные блоки. По умолчанию в качестве имени перехода используется название блока. Однако, имеется возможность дать ему другое имя. Надписывание перехода производится так же, как и надписывание позиции.
После того, как переход подписан в левом нижнем углу блока появляется квадрат, который подтверждает, что блок подписан.
Аналогичным образом устанавливаются для перехода защита, кодовый сегмент и задержка.
Защита запрещает переход в соответствии с условиями на переменные, указанные в выражениях смежных дуг. Для ее установки требуется создать метку, содержащую выражение для защиты, затем командой "Guard" меню CPN она привязывается к переходу.
Кодовый сегмент определяет сегмент в коде Standard ML, который выполняется в эмуляторе Design/CPN всякий раз, когда будет срабатывать переход.
Задержка определяет время, которое характеризует продолжительность срабатывания перехода.
6. Надписывание дуг.
Каждая дуга может иметь свое имя и выражение, которые задаются как присоединяемые метки.
Для указания имени дуги необходимо создать новую метку, затем вызвать команду "Place Name" меню CPN и указать на маленький невидимый квадратик, принадлежащий функциональному блоку и расположенный в месте соединения блока и дуги.
Выражение дуги характеризует мультинабор фишек, которые двигаются по дуге при любом срабатывании перехода, являющегося входным для дуги. Присоединение осуществляется аналогично вызовом пункта "Arc Expression" меню CPN.
7. Удаление и скрытие динамической модели.
Для скрытия элементов динамической модели используется команда "Hide CPN De-tail" меню CPN. Чтобы сделать элементы снова видимыми требуется команда "Show CPN Detail". Чтобы полностью удалить позиции сети Петри используется команда "Discard CPN Places". [9]
§5. Применение сетевых моделей для описания параллельных процессовПри анализе сети Петри основное внимание уделяется, как правило, трем направлениям.
Проблема достижимости. В сети Петри с начальной разметкой М0 требуется определить, достижима ли принципиально некоторая разметка М' из М0. С точки зрения исследования моделируемой системы, эта проблема интерпретируется как проблема достижимости (реализуемости) некоторого состояния системы.
Оценка живости переходов сети. Под живостью перехода понимают возможность его срабатывания в данной сети при начальной разметке М0. Анализ модели на свойство живости позволяет выявить невозможные состояния в моделируемой системе (например, неисполняемые ветви в программе).
Оценка безопасности сети. Безопасной является такая сеть Петри, в которой ни при каких условиях не может появиться более одной метки в каждой из позиций. Для исследуемой системы это означает возможность функционирования ее в стационарном режиме. На основе анализа данного свойства могут быть определены требования к буферным накопителям в системе.
Итак, достоинства сетей Петри заключаются в следующем:
позволяют моделировать ПП всех возможных типов с учетом возможных конфликтов между ними;
обладают наглядностью и обеспечивают возможность автоматизированного анализа;
позволяют переходить от одного уровня детализации описания системы к другому (за счет раскрытия/закрытия переходов).
Вместе с тем, сети Петри имеют ряд недостатков, ограничивающих их возможности. Основной из них - время срабатывания перехода считается равным нулю, что не позволяет исследовать с помощью сетей Петри временные характеристики моделируемых систем. [8]
Е - сети. В результате развития аппарата сетей Петри был разработан ряд расширений. Одно из наиболее мощных - так называемые Е-сети (evaluation - "вычисления", "оценка") - "оценочные сети". В отличие от сетей Петри, в Е-сетях:
имеются несколько типов вершин-позиций: простые позиции, позиции-очереди, разрешающие позиции;
фишки (метки) могут снабжаться набором признаков (атрибутов);
с каждым переходом может быть связана ненулевая задержка и функция преобразования атрибутов фишек;
введены дополнительные виды вершин-переходов;
в любую позицию может входить не более одной дуги и выходить также не более одной.
В связи с этим любой переход может быть описан тройкой параметров:
dj= (S,t (dj),p (dj)).
Здесь S - тип перехода, t (dj) - функция задержки, отражающая длительность срабатывания перехода, р (dj) - функция преобразования атрибутов меток. Еще одно важное отличие Е-сетей от сетей Петри состоит в том, что метки интерпретируются как транзакты, перемещающиеся по сети, а вершины-переходы трактуются как устройства, выполняющие ту или иную обработку транзактов. Следствием такого подхода является требование: ни одна вершина-позиция Е-сети не может содержать более одной метки (то есть, любая Е-сеть изначально является безопасной). Базовые переходы Е-сети описаны ниже.
Т-переход ("исполнение", "простой переход"). Его графическое представление аналогично представлению вершины-перехода сети Петри (рис.4, слева). Переход срабатывает при наличии метки во входной позиции и отсутствии ее в выходной позиции. Формально это можно записать так:
(1; 0) | - (0;1).
Т-переход позволяет отразить в модели занятость некоторого устройства (подсистемы) в течение некоторого времени, определяемого параметром t (d). F-nepexod ("разветвление"). Графическое представление приведено на рис.4 в центре. Срабатывает при тех же условиях, что и Т-переход:
С содержательной точки зрения, F-переход отображает разветвление потока информации (транзактов) в системе.
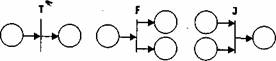
Рис.4. Графическое представление переходов Е-сети - Т-переход (слева), F-переход (в центре), J-переход (справа) J-переход ("объединение"). Графическое обозначение показано на рис.4 справа. Переход срабатывает при наличии меток в обеих входных позициях и отсутствии метки в выходной позиции: (1,1; 0) | - (0,0;1)
Он моделирует объединение потоков или наличие нескольких условий, определяющих некоторое событие.
Х-переход ("переключатель"). По сравнению с тремя предыдущими типами переходов, он содержит дополнительную управляющую ("разрешающую") позицию, которая графически обозначается обычно либо квадратиком, либо шестиугольником (рис.5, слева). Рис.5. Графическое представление переходов Е-сети, имеющих разрешающую позицию - Х-переход.
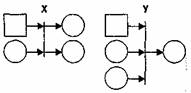
Рис.5. Графическое представление переходов Е-сети, имеющих разрешающую позицию - Х-переход (слева), Y-переход (справа)
Логика его срабатывания задается следующими соотношениями:

Х-переход изменяет направление потока информации (транзактов). В общем случае разрешающая процедура может быть сколь угодно сложной, но сущность ее работы заключается в проверке выполнения условий разветвления потока (с точки зрения программиста, разрешающая позиция аналогична условной инструкции типа if).
Y-переход ("выбор", "приоритетный выбор"). Этот переход также содержит разрешающую позицию (рис.5, справа). Логика срабатывания Y-перехода:

Y-переход отражает приоритетность одних потоков информации (транзактов) по сравнению с другими. При этом разрешающая процедура может быть определена различным образом: как операция сравнения фиксированных приоритетов меток; как функция от атрибутов меток (например, чем меньше время обслуживания, тем выше приоритет). В некотором смысле он работает аналогично инструкции выбора типа case. [12]
Еще раз подчеркнем, что в Е-сети все переходы обладают свойством безопасности. Это означает, что в выходных позициях (которые, в свою очередь, могут быть входными для следующего перехода) никогда не может быть более одной метки. Вместе с тем, в Е-сетях существуют понятия макроперехода и макропозиции, которые позволяют отображать в модели процессы накопления обслуживаемых транзактов в тех или иных узлах системы, а также расширить логические возможности Е-сетей.
Рассмотрим некоторые из них.
Макропозиция очередь представляет собой линейную композицию Т-переходов; суммарное количество выходных вершин-позиций определяет "емкость" очереди. Макропозиция генератор позволяет представлять в сети источник меток (транзактов).
Если необходимо задать закон формирования меток, то "генератор" может быть дополнен разрешающей позицией.
Поскольку в Е-сети нельзя "накапливать" метки, то вводится макропозиция поглощения (или аккумулятор).
В целях повышения компактности и наглядности Е-сети для обозначения макропозиций используют специальные символы:
Q-очередь;
G - генератор;
А - аккумулятор.
Аналогичным образом, путем композиции N однотипных переходов могут быть получены макропереходы всех типов: XN, YN, JN.
Рассмотренные особенности Е-сетей существенно расширяют их возможности для моделирования дискретных систем вообще и параллельных процессов в частности. Ниже приведен пример описания в виде Е-сети мультипрограммной вычислительной системы (Рис.6). Обработка поступающих заданий организована в ней по принципу квантования времени: каждому заданию выделяется равный отрезок (квант) процессорного времени; если задание выполнено, то оно покидает систему, если же времени оказалось недостаточно, то задание встает в очередь и ждет повторного выделения кванта времени.
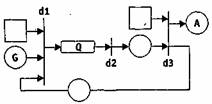
Рис.6. Пример описания вычислительной системы в виде Е-сети
На рисунке использованы следующие обозначения:
d1 - постановка задания в очередь;
d2 - выполнение задания в течение одного кванта времени;
d3 - анализ степени завершенности задания.
Помимо очевидных достоинств Е-сетей, проявленное к ним внимание объясняется еще и тем, что технология моделирования систем в виде Е-сетей весьма эффективно реализуется с помощью инструмента S1MULINK, входящего в состав пакета MATLAB. [10]
§6. Моделирование процесса обучения с помощью вложенных сетей Петри
Вложенные сети Петри (Nested Petri Nets - NPN) - один из современных инструментов моделирования и исследования параллельно работающих систем, обладающих определенной независимостью и собственной активностью. Эти черты делают привлекательным их использование при моделировании учебного процесса, проводимого группой обучаемых как в традиционном учебном процессе, так и при интерактивном компьютерном обучении. В данной работе впервые предлагается двухуровневая модель обучения, состоящая из центральной системы и набора систем-сателлитов, моделирующих индивидуальное поведение учащихся.
Интерактивное, т.е. в значительной мере самостоятельное обучение с использованием современных информационных технологий одно из важнейших направлений совершенствования системы образования, в том числе я в России. Быстрое развитие телекоммуникаций, и в особенности сети Интернет создало технологическую основу для обмена информацией между организациями и отдельными лицами, вне зависимости от их социального статуса, государственной принадлежности, географического положения, и явилось мощным стимулом развития дистанционного образования.
В настоящее время, несмотря на значительные успехи интерактивного обучения, существует немало нерешенных проблем. К ним мы в первую очередь относим разработку инженерных методов создания систем компьютерного обучения как своеобразных информационных систем с использованием современных методологий и технологий разработки, в частности, САSЕ - технологий. Кроме того, актуально создание методов априорной оценки дидактических и эксплуатационных характеристик разрабатываемых обучающих систем. Решение указанных проблем предполагает наличие моделей, адекватно описывающих все стороны процесса обучения - функциональных, информационных, динамических. Для описания динамики процесса обучения были предложены модели, основанные на формализме сетей Петри и на тесно связанной с ним теории цепей Маркова. Однако предложенные ранее модели описывали только взаимодействие отдельного учащегося с обучающей системой. В то же время в современном образовании важную роль играет умение учащихся работать в коллективе, взаимодействовать при выполнении проектов. Один из возможных путей к моделированию процессов коллективной работы учащихся связан, на наш взгляд, с применением сравнительно нового класса сетевых моделей - вложенных сетей Петри.
Данная работа посвящена изложению основных принципов моделирования распределенных систем с помощью указанного формализма. В первой части работы приведены краткие сведения по теории таких сетей. Во второй части предложена простая модель взаимодействия учащегося с обучающей системой и другими учащимися.
Вложенные сети Петри.
Рассмотрим расширение сетей Петри, которое оказывается полезным при моделирования учебного процесса. Речь идет о так называемых вложенных сетях Петри (Nested Petri Nets - NPN).
Появление указанной разновидности сетей Петри связано с желанием исследователей иметь инструмент для адекватного и удобного представления систем со сложной иерархической и мультиагентной структурой.
Вложенные сети Петри представляют собой расширение стандартного формализма сетей Петри, в котором фишки, представляющие локальные ресурсы в позициях системной сети, сами могут быть сложными объектами с сетевой структурой и моделироваться сетями Петри нижнего уровня - их мы будем называть сателлитными сетями.
Структурно такая сеть состоит из системной сети SN и набором сетей-фишек (сателлитов) ЕNi, i= 1,…, n. При этом между некоторыми переходами системной сети, и переходами сетей-фишек может быть установлена связь, разрешающая только их совместное срабатывание. Такие переходы называются помеченными.
Функционирование сетей, входящих в NPN, в значительной мере совпадает с функционированием традиционных сетей Петри. Отличие составляют механизмы синхронизации работы сетей Петри различного уровня. В связи с этим в NPN различают следующие четыре вида шагов срабатывания.
Системно-автономный шаг, который соответствует срабатыванию непомеченного перехода в системной сети;
Сателлитно-автономный шаг, который соответствует срабатыванию непомеченного перехода в сети - фишке ЕNi;
Шаг горизонтальной синхронизации, при котором одновременно срабатывают переходы в сетях - фишках ЕNi, помеченные одинаковыми метками;
Шаг вертикальной синхронизации, при котором одновременно срабатывают переходы в системной сети SN и сетях - фишках ЕNi, имеющие одинаковые метки.
Разумеется, при этом предполагается, что во всех сетях все участвующие в работе переходы являются активными, т.е. в их входных позициях имеются необходимые для срабатывания ресурсы.
Пример вложенной сети Петри рассмотрен ниже.
Модель процесса интерактивного обучения с использованием вложенных сетей Петра.
Проиллюстрируем возможности вложенных сетей Петри для получения модели процесса обучения с подсистемами различного уровня. Рассмотрим модель процесса интерактивного обучения показанная на рис.7. В этой модели каждый обучаемый моделируется одной фишкой, обозначаемой переменной var s: STUDENT, которая соответствует целочисленному коду обучаемого. При этом информация об истории прохождении курса конкретным студентом теряется после того, как процесс обучения завершен. Кроме того, в модели на рис.7 отсутствует возможность дифференцированного оценивания успешности обучения. Также не предусмотрена возможность неудачного завершения курса, поскольку число попыток изучения материала и тестирования не ограничено. И, наконец, нет возможности моделировать взаимодействие учащихся.
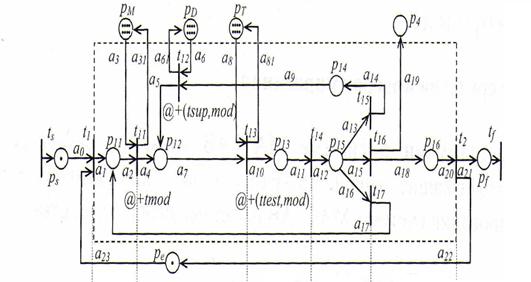
Подготовка Обучение Тестирование Оценивание Принятие решения
Рис.7. Системная сеть SN - раскрашенная сеть Петри с временным и вероятностным механизмами, моделирующая прохождение учебного курса
Функциональность системы можно повысить, если моделировать поведение каждого обучаемого с помощью отдельной сети Петри. Тогда фишка, обозначаемая переменной s, станет сетью ЕNs, где s - код обучаемого, как принято на рис.7.
При этом получится вложенная сеть Петри, которая состоит из системной сети SN (она изображена на рис.7) и набора сателлитных сетей ЕNs, (s=1,2,. .). Один из возможных вариантов сети ЕNs представлен на рис.8.
Кратко поясним работу вложенной сети. На рис.8 позиции обозначены буквами qi, i = 1,…,10. Смысл позиций q1,…,q6 совпадает со смыслом позиций p11,…,p16 на рис.7, остальные позиции относятся к оценке успешности обучения. Переходы t1,t11,…,t17 на обоих рисунках имеют один и тот же смысл. При этом черта над обозначением перехода на рис.8 означает наличие вертикальной синхронизации: одноименные переходы могут сработать только одновременно. Это означает синхронизацию следующих действий:
приход обучаемого в систему (срабатывание перехода t1), создание в системной сети SN сателлитной сети ЕNs, в виде фишки s; в свою очередь, в сателлитной сети переменная s относится к цветовому множеству STUDENT;
выбор учебного модуля и начало процесса обучения срабатывание переходов t11;
завершение процесса обучения и выбор тестов срабатывание переходов t13;
завершение процесса тестирования и переход к оцениванию - срабатывание переходов t14;
принятие решения по результатам тестирования - срабатывание переходов: t15 - изучение дополнительного материала, t16 - завершение изучения модуля, t17 - повторное изучение всего материала.
Кроме описанных событий сеть ЕNs, позволяет оценить количество баллов, набранных учащимся в процессе изучения модуля. Для этого введены дополнительные ресурсы, задаваемые цветовыми множествами:
Color BALL = integer;
Color FAILURE = Вооlеаn;
и соответствующие переменные:
var β: BALL, var γ: FAILURE.
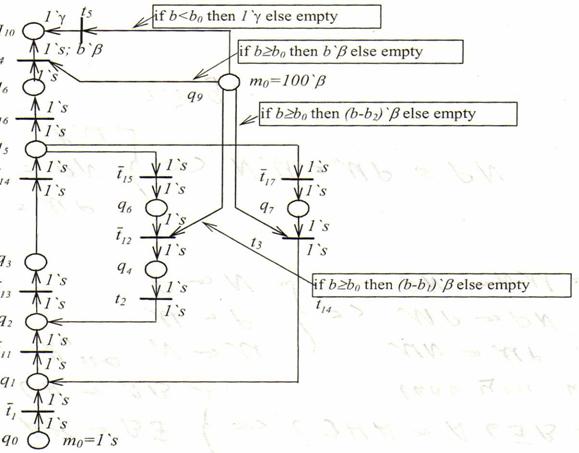
Рис.8. Вложенная сеть Еs
Переменная β означает количество баллов, набранных учащимся при выполнении модуля. Первоначально в позиции q9 находится 100 баллов, а затем при каждой неудаче маркировка этой позиции уменьшается: при необходимости изучения дополнительного материала - на b1 баллов, а при необходимости повторного изучения всего курса - на b2 баллов. При успешном завершении процесса обучения срабатывает переход t5, и в позицию с передается набранное учащимся количество баллов - число b.
Минимальное число баллов, при котором возможна положительная оценка, составляет b0 баллов. Если текущее значение величины β окажется меньше b0, то процесс обучения признается неудачным, и переменная γ принимает значение true, которое передается в позицию q10 при срабатывании перехода t5. Все остальные переходы при этом оказываются заблокированными.
В рассмотренном примере показана только вертикальная синхронизация, которая заключается в требовании одновременного срабатывания переходов в сетях SN и Еs. Возможно предусмотреть и горизонтальную синхронизацию между сетями Еs, что позволило бы моделировать совместную работу учащихся, например при выполнении коллективного проекта.
Итак, мы видим, что использование вложенных сетей Петри расширяет возможность моделирования обучающих систем и позволяет проводить ранее недоступные исследования.
Разумеется, практическое использование предложенной модели возможно только при наличии соответствующего программного обеспечения, которое в настоящий момент разрабатывается. [13]
Заключение
Итогом курсовой работы стали математические модели с использованием сетей Петри, построение динамических моделей на основе сетей Петри, применение сетевых моделей с использованием сетей Петри. Сети Петри являются эффективным инструментом дискретных процессов, в частности, функционирования станочных систем. Разработаны теории моделирования с помощью сетей Петри. В данной работе приведены примеры моделей, программа. Было рассмотрено сетевое планирование как метод управления, основанный на использовании математического аппарата теории графов и системного подхода для отображения и алгоритмизации комплексов взаимосвязанных работ, действий или мероприятий для достижения четко поставленной цели. Информацию по теме можно использовать из Интернета, а информацию по "математической части" в пособиях и учебниках по данной теме.
В ходе курсовой работы была изучена литература по теме (Интернет - источники). Было установлено, что некоторые виды сетей можно реализовать с помощью пакета MATLAB.
Список используемой литературы
1. <http://mathmod. narod.ru/> (октябрь, 2008);
2. <http://matlab. exponenta.ru/ml/book1/matlab/index_book. php> (октябрь, 2008);
3. <http://www.rgc. su/material/998/0/index. shtml > (декабрь, 2008);
4. <http://www.vismat.ru/osnovy-tehnologii-imitacionnogo-modelirovaniya/primenenie-setevyh-modeley-dlya-opisaniya-paralle> (ноябрь, 2008);
5. <http://revolution. /mathematics/00003923_0.html> (ноябрь, 2008);
6. <http://orion.netlab. cctpu.edu.ru/TPU/soft/10. htm> (декабрь, 2008);
7. <http://www.miracle.ru/pub/512/512. htm> (декабрь, 2008);
8. <http://orion.netlab. cctpu.edu.ru/TPU/soft/10. htm> (октябрь, 2008);
9. <http://www.netspetri. h17.ru/theor.html> (октябрь, 2008);
10. 10) <http://ru. wikipedia.org/wiki/%D0%A1%D0%B5%D1%82%D0%B8_%D0%9F%D0%B5%D1%82%D1%80%D0%B8> (декабрь, 2008);
11. 11) <http://www.gpss.ru/paper/ryzhikov1/9.html> (октябрь, 2008);
12. <http://www.mipt.ru/nauka/f_228ed/a_3l9ed.html> (декабрь, 2008);
13. <http://lib. krasu.ru/resources. php3? menu1=socvest&menu2=2006-4> (декабрь, 2008).
Похожие работы
... целом как сложной системы в различных условиях. Вычислительные эксперименты с математическими моделями дают исходные данные для оценки показателей эффективности объекта. Поэтому математическое моделирование как методология организации научной экспертизы крупных проблем незаменимо при проработке народнохозяйственных решений. (В первую очередь это относится к моделированию экономических систем[6]). ...
... базису, состоящему всего из одной функции. Были построены комбинационные схемы, иллюстрирующие полученные результаты. Выгода рассмотренных преобразований функций становится очевидной при их практической реализации на стандартизованных электронных микросхемах. 2 Синтез конечных автоматов 2.1 Постановка задачи Конечный автомат задан своими уравнениями переходов и ...
... дипломной работе рассматриваются математические модели и методы реализации этих двух направлений. Дипломная работа состоит из 3 глав, приложения, литературы и заключения. Глава 1. Математическое моделирование роста доходности страховых компаний §1 Общая характеристика основных фактов и понятий при моделировании деятельности страховых компаний Рассматривается страховая компания, в которой ...
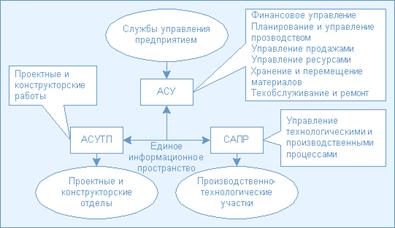
... подхода к решению задачи. Метод – систематизированная совокупность шагов, действий, которые необходимо предпринять, чтобы решить определенную задачу или достичь определенной цели. При исследовании методов автоматизации управления электронным предприятием необходимо заметить, что основным элементом управления на любом предприятии является документ. Фактором, влияющим на хождение документа внутри ...

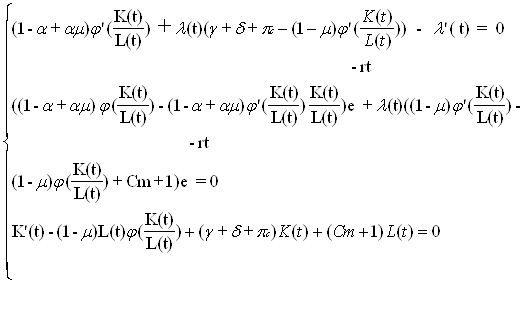

0 комментариев