Теория помехоустойчивого кодирования занимается поиском кодов, повышающих достоверность передачи информации в каналах с помехами

2. Теория помехоустойчивого кодирования занимается поиском кодов, повышающих достоверность передачи информации в каналах с помехами.

 

3. Способы представления кодов

В зависимости от применяемых методов кодирования, используют различные математические модели кодов, при этом наиболее часто применяется представление кодов в виде: кодовых матриц; кодовых деревьев; многочленов; геометрических фигур и т.д.

 

3.1 Матричное представление кодов

Используется для представления равномерных n - значных кодов. Для примитивного (полного и равномерного) кода матрица содержит n - столбцов и 2^{n -} строк, т.е. код использует все сочетания. Для помехоустойчивых (корректирующих, обнаруживающих и исправляющих ошибки) матрица содержит n - столбцов (n = k+m, где k-число информационных, а m - число проверочных разрядов) и 2^{k -} строк (где 2^{k -} число разрешенных кодовых комбинаций). При больших значениях n и k матрица будет слишком громоздкой, при этом код записывается в сокращенном виде. Матричное представление кодов используется, например, в линейных групповых кодах, кодах Хэмминга и т.д.

 

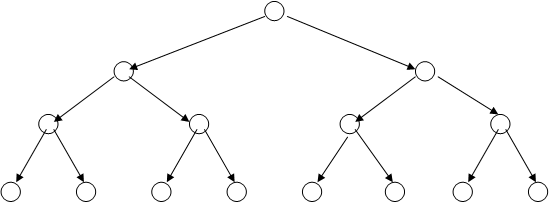
3.2 Представление кодов в виде кодовых деревьев

 

Кодовое дерево - связной граф, не содержащий циклов. Связной граф - граф, в котором для любой пары вершин существует путь, соединяющий эти вершины. Граф состоит из узлов (вершин) и ребер (ветвей), соединяющих узлы, расположенные на разных уровнях. Для построения дерева равномерного двоичного кода выбирают вершину называемую корнем дерева (истоком) и из нее проводят ребра в следующие две вершины и т.д.

Пример кодового дерева для полного кода приведен на рис.1.

1 0

1 0 1 0

1 0 1  0 1 0 1 0

111 110 101 100 011 010 001 000

Рис.1. Дерево для полного двоичного кода при n = 3

Дерево помехоустойчивого кода строится на основе дерева полного кода путем вычеркивания запрещенных кодовых комбинаций. Для дерева неравномерного кода используется взвешенный граф, при этом на ребрах дерева указываются вероятность переходов. Представление кода в виде кодового дерева используется, например, в кодах Хаффмена.

 

3.3 Представление кодов в виде многочленов

Представление кодов в виде полиномов основано на подобии (изоморфизме) пространства двоичных n - последовательностей и пространства полиномов степени не выше n - 1.

Код для любой системы счисления с основанием Х может быть представлен в виде:

 

G (x) = a_n-1 x^n-1+ a_n-2 x^n-2+... + a₁ x+ a₀ =,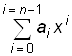

где а_i - цифры данной системы счисления (в двоичной 0 и 1);

х - символическая (фиктивная) переменная, показатель степени которой соответствует номерам разрядов двоичного числа_-

Например: Кодовая комбинация 1010110 может быть представлена в виде:

G (x) =1×x⁶+0×x⁵+1×x⁴+0×x³+1×x²+1×x¹+0×x⁰ =x⁶+x⁴+x²+x=10101

При этом операции над кодами эквивалентны операциям над многочленами. Представление кодов в виде полиномов используется например, в циклических кодах.

 

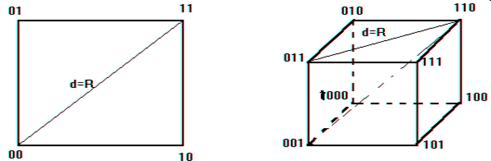
3.4 Геометрическое представление кодов

Любая комбинация n - разрядного двоичного кода может быть представлена как вершина n - мерного единичного куба, т.е. куба с длиной ребра равной 1. Для двухэлементного кода (n = 2) кодовые комбинации располагаются в вершинах квадрата. Для трехэлементного кода

(n = 3) - в вершинах единичного куба (рис.2).

В общем случае n мерный куб имеет 2ⁿ вершин, что соответствует набору кодовых комбинаций 2^n.

n = 2 n = 3

Рис.2. Геометрическая модель двоичного кода

Геометрическая интерпретация кодового расстояния. Кодовое расстояние - минимальное число ребер, которое необходимо пройти, чтобы попасть из одной кодовой комбинации в другую. Кодовое расстояние характеризует помехоустойчивость кода.

Список литературы

1.         Кловский Д.Д. Теория передачи сигналов. -М.: Связь, 1984.

2.         Кудряшов Б.Д. Теория информации. Учебник для вузов Изд-во ПИТЕР, 2008. - 320с.

3.         Рябко Б.Я., Фионов А.Н. Эффективный метод адаптивного арифметического кодирования для источников с большими алфавитами // Проблемы передачи информации. - 1999. - Т.35, Вып. - С.95 - 108.

4.         Семенюк В.В. Экономное кодирование дискретной информации. - СПб.: СПбГИТМО (ТУ), 2001

5.         Дмитриев В.И. Прикладная теория информации. М.: Высшая школа, 1989.

6.         Нефедов В.Н., Осипова В.А. Курс дискретной математики. М.: МАИ, 1992.

7.         Колесник В.Д., Полтырев Г.Ш. Курс теории информации. М.: Наука, 2006.