Класифікація криптоперетворень

3. Класифікація криптоперетворень

Найбільш загальною наукою про таємницю є криптологія. Криптологія як наука вивчає закономірності забезпечення конфіденційності, цілісності і т.д. критичної інформації в умовах інтенсивної протидії (криптоаналізу).

				Криптологія
								Криптоаналіз
	Криптографія

Криптографія – вивчає методи, алгоритми і засоби здійснення криптографічного захисту інформації.

Криптоаналіз – вивчає методи, алгоритми і засоби розкриття криптографічної системи при невідомій частині ключа.

Криптографічне перетворення інформації – здійснюється з використанням симетричних, несиметричних криптосистем. Криптографічна система називається симетричною, якщо ключ прямого перетворення збігається з ключем зворотного перетворення чи обчислюється один з іншого не вище чим з поліноміальною складністю (не більш 1 секунди).

Криптосистема (алгоритм) називається симетричною, якщо ключ прямого перетворення збігається з ключем зворотного перетворення:

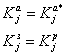(7)

Криптосистема (алгоритм) називається асиметричний, якщо ключ прямого перетворення не збігається з ключем зворотного перетворення:

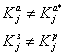(8)

або може бути обчислений один при знанні іншого не нижче ніж з субекспоненціальною складністю.

1. Для захисту інформації, як правило, використовуються криптоперетворення.

2. Стійкість перетворень забезпечується використанням ключових даних.

3. Ключові дані можна розділити на два класи відносно симетричності та асиметричності.

4. В асиметричних криптоперетвореннях один із ключів може бути відкритим.

В Європейському проекті NESSIE–2000-2003 визначено 10 видів криптоперетворень.

Симетричні – розробка блокового симетричного шифрування, потоковий шифр, автентифікація (процедура встановлення дійсності джерела, приймача повідомлень).

Несиметричні – функції гешування (обчислення криптографічних контрольних сум) односпрямованої геш (стиску з великого простору в малий), ключова геш з використанням ключа.

Направлене шифрування (виконується умова (2)).

Ідентифікація (автентифікація) - (1),(2).

Криптопротокол – рішення розподіленої задачі, багатоетапно.

4. Модель крипто аналітика

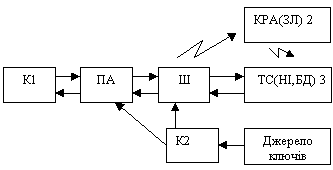Рисунок 3

Користувач К1 – джерело інформаційних повідомлень M_i, розмір джерела (кількість повідомлень) . Розмір ймовірності появлення повідомлення Р(M_i) апріорна ентропія Н(M_i) джерела інформації. З метою забезпечення цілісності і дійсності повідомлення M_i піддається криптоперетворенню – автентифікації, на виході формується M_i.

(9)

Для забезпечення конфіденційності,  повідомлення 2 піддається зашифровуванню, на виході формується С_j – криптограма.

(10)

К_j ключ (обраний із простору ключів, розмірність ) з’являється випадково, тому на виході шифратора з’являється під його дією криптограма.

С_j передається К2 через ТС по відкритому каналу, чи записується на носій інформації.

Задачі, що ставить криптоаналіз:

1) визначити яке повідомлення міститься в криптограмі;

2) відновити K_j ключ.

При криптоаналізі вважають, що криптоаналітик знає все систему (апріорну статистику, режими роботи, загальні характеристики). При імовірнісному підході криптоаналітик можде будувати модель апостеріорного ряду

 ,  (11)

Перший імовірнісний підхід до криптоаналізу: обчислюється . Недолік такого підходу в тому, що ряд  дуже великий і його практично розв’язати неможливо.

На визначеність криптоаналітиком того, яке повідомлення М_і міститься в криптограмі С_і можна задати через умовну ентропію . Таку ентропію можна обчислити як:

(12)

На початку криптоаналізу відома ентропія Н(М), після того, як ведеться криптоаналіз ентропія зменшується .

Будемо вважати, що криптоаналітик отримав від джерела інформації

(13)

Граничні ситуації:

якщо  = 0, ;

якщо , .

Реальна ситуація:

Аналізуючи криптоаналітик або рішає задачу криптоаналізу, або ні.  обчислюється за допомогою (12)

В якості оцінки стійкості, як правило, використовуються:

1)         N_k – кількість ключів, що дозволені в системі.

2)         H(k) – ентропія джерела ключів:

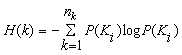, (14)

де - імовірність появи К_j ключа в системі.

3)                                                                 t_б – безпечний час (математичне сподівання часу розкриття криптосистеми із використанням конкретного методу):

, (15)

де N_k – кількість групових операцій, які повинен розглянути криптоаналітик;

 γ – потужність криптоаналітичної системи (вар/с)

К – кількість секунд у році: (с/рік)

 – імовірність розкриття.

4)         l₀- відстань єдності шифру.

Множина параметрів, за якою буде оцінена складність криптоаналізу:

(16)

В залежності від складності задачі криптоаналізу, шифри розподіляються на чотири класи:

1) безумовно стійкі або теоретично недешифруємі (відносно яких криптоаналітик ніколи не зможе виконати криптоаналіз);

2) обчислювально стійкі (в принципі розкрити можна, але не достатньо ресурсів для розкриття);

3) ймовірностійкі;

4) обчислювально нестійкі.

В безумовно та обчислювально стійких шифрах безпечний час набагато більше за цілісність інформації:

, (17)

а в обчислювально нестійких шифрах:

. (18)

5. Умови реалізації безумовно стійких криптосистем

Теорема Необхідною і достатньою умовами забезпечення безумовної стійкості є:

, (19)

тобто імовірність появи С_j на виході шифратора не повинно залежати від того, яке М_і повідомлення з’явилось на виході джерела повідомлення.

Інакше, ймовірність появлення криптограми повинно бути однаковою для всіх ключів і для всіх повідомлень. Фізично це означає, що будь-яке повідомлення може відображатись в будь-яку криптограму з однаковою ймовірністю.

Доведення: визначимо імовірність, що може обчислити криптоаналітик:

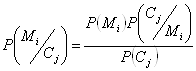. (20)

Криптоаналітик не одержить ніякої інформації відносно джерела повідомлення, якщо:

, (21)

. (22)

Умову безумовної стійкості можна вважати (20) або (21).

З виразу (22):

.

Теорему доведено.