Навигация
Обратный S-блок приведен в таблице 6
Таблица 6. Значения обратного S-блока
| 82 | 9 | 106 | 213 | 48 | 54 | 165 | 56 | 191 | 64 | 163 | 158 | 129 | 243 | 215 | 251 |
| 124 | 227 | 57 | 130 | 155 | 47 | 255 | 135 | 52 | 142 | 67 | 68 | 196 | 222 | 233 | 203 |
| 84 | 123 | 148 | 50 | 166 | 194 | 35 | 61 | 238 | 76 | 149 | 11 | 66 | 250 | 195 | 78 |
| 8 | 46 | 161 | 102 | 40 | 217 | 36 | 178 | 118 | 91 | 162 | 73 | 109 | 139 | 209 | 37 |
| 114 | 248 | 246 | 100 | 134 | 104 | 152 | 22 | 212 | 164 | 92 | 204 | 93 | 101 | 182 | 146 |
| 108 | 112 | 72 | 80 | 253 | 237 | 185 | 218 | 94 | 21 | 70 | 87 | 167 | 141 | 157 | 132 |
| 144 | 216 | 171 | 0 | 140 | 188 | 211 | 10 | 247 | 228 | 88 | 5 | 184 | 179 | 69 | 6 |
| 208 | 44 | 30 | 143 | 202 | 63 | 15 | 2 | 193 | 175 | 189 | 3 | 1 | 19 | 138 | 107 |
| 58 | 145 | 17 | 65 | 79 | 103 | 220 | 234 | 151 | 242 | 207 | 206 | 240 | 180 | 230 | 115 |
| 150 | 172 | 116 | 34 | 231 | 173 | 53 | 133 | 226 | 249 | 55 | 232 | 28 | 117 | 223 | 110 |
| 71 | 241 | 26 | 113 | 29 | 41 | 197 | 137 | 111 | 183 | 98 | 14 | 170 | 24 | 190 | 27 |
| 252 | 86 | 62 | 75 | 198 | 210 | 121 | 32 | 154 | 219 | 192 | 254 | 120 | 205 | 90 | 244 |
| 31 | 221 | 168 | 51 | 136 | 7 | 199 | 49 | 177 | 18 | 16 | 89 | 39 | 128 | 236 | 95 |
| 96 | 81 | 127 | 169 | 25 | 181 | 74 | 13 | 45 | 229 | 122 | 159 | 147 | 201 | 156 | 239 |
| 160 | 224 | 59 | 77 | 174 | 42 | 245 | 176 | 200 | 235 | 187 | 60 | 131 | 83 | 153 | 97 |
| 23 | 43 | 4 | 126 | 186 | 119 | 214 | 38 | 225 | 105 | 20 | 99 | 85 | 33 | 12 | 125 |
2.3 ПРЕОБРАЗОВАНИЕ ShiftRow
Следующий шаг раунда - перестановка байтов в блоке. Порядок байтов меняется в строке (bi,0, bi,1, bi,2,..., bi,Lb-1) структуры В в соответствии с таблицами 7-9.
Операция ShiftRow для блоков длины 128 бит (Lb = 4)
|
| ||||||||||||||||||||||||||||||||||||||||
Операция ShiftRow для блоков длины 192 бит (Lb = 6)
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Операция ShiftRow для блоков длины 256 бит (Lb = 8)
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Все нулевые строки остаются без изменений. В строках i = 1,2,3 байты циклически сдвигаются влево на cLb, i позиций: с позиции с номером j на позицию с номером j - cLb, i mod Lb, где значение cLb, i определяется по таблице 10.
Таблица 10. Размер сдвига строк в операции ShiftRow
| Lb | cLb,1 | cLb,2 | cLb,3 |
| 4 | 1 | 2 | 3 |
| 6 | 1 | 2 | 3 |
| 8 | 1 | 3 | 4 |
При обратном преобразовании позиция с номером j в строках i = 1,2,3 сдвигается на позицию с номером j + cLb, i mod Lb.
2.4 ПРЕОБРАЗОВАНИЕ MixColumnПосле того как выполнена последняя построчная перестановка, на следующем шаге каждый столбец (bi,j) блока текста, где i = 0,...,3, j = 0,...,Lb, представляется в виде полинома над полем F28 и умножается на фиксированный полином a (x) = а3x3 + а2x2 + а1x + a0скоэффициентами a0 (x) =x, a1 (x) = 1, a2 (x) = 1, a3 (x) = х + 1. Затем вычисляется остаток от деления полученного произведения на модуль М (х) = х4 + 1. Таким образом, каждый байт столбца взаимодействует со всеми остальными байтами столбца. При построковом преобразовании ShiftRow на каждом раунде байты взаимодействуют друг с другом в других комбинациях. То есть эти две операции дают сильное перемешивание.
Этот шаг можно свести к умножению на матрицу:

Умножение на '02' (соответственно на х) мы уже реализовали в виде функции xtime (см. таблицу 3). Умножение на '03' (соответственно на х + 1) тоже сделано по аналогии.
Для обращения преобразования MixColumn умножаем каждый столбец (bi,j) блока текста на полином г (х) = r3х3 + r2х2 + r1х + r0 с коэффициентами r0 (х) =х3 + х2 + х, r1 (х) = х3 + 1, r2 (х) = х3 + х2 + 1, r3 (х) = х3 + х + 1 и приводим результат по модулю М (х) = х4 + 1. Соответствующая матрица имеет вид:

На последнем шаге цикла раундовый ключ складывается по модулю 2 с блоком текста:
![]()
Зашифрование по алгоритму Rijndael реализуется в виде следующего псевдокода. Аргументы обрабатываются как указатели на поля байтов или четырехбайтовых слов. Интерпретация полей, переменных и функций дана в таблицах 11-13.
Таблица 11
Интерпретация переменных
| Переменные | Интерпретация |
| Nk | Длина Lk секретного ключа пользователя в четырехбайтовых словах |
| Nb | Длина Lb блока в четырехбайтовых словах |
| Nr | Число раундов Lrв соответствии с таблицами выше |
Таблица 12
Интерпретация полей
| Переменные | Размер в байтах | Интерпретация |
| CipherKey | 4*Nk | Секретный ключ пользователя |
| ExpandedKey | 4*Nb* (Nr+1) | Поле четырехбайтовых слов под развертку ключа |
| Rcon | é4*Nb* (Nr+1) /Nkù | Поле четырехбайтовых слов под константы c (j) = (rc (j), 0, 0, 0) |
| State | 4*Nb | Поле ввода открытого текста и вывода зашифрованного текста |
| RoundKey | 4*Nb | Раундовый ключ, фрагмент ExpandedKey |
Таблица 13
Интерпретация функций
| Функция | Интерпретация |
| KeyExpansion | Генерация раундового ключа |
| RotByte | Сдвиг четырехбайтового слова влево на 1 байт: (abcd) ® (bcda) |
| ByteSub | Подстановка в S-блоке всех байтов поля |
| Round | Обычный раунд |
| FinalRound | Последний раунд без преобразования MixColumn |
| ShiftRow | Преобразование ShiftRow |
| MixColumn | Преобразование MixColumn |
| AddRoundKey | Сложение с ключом раунда |
Генерация ключа при Lk < 8:
KeyExpansion (byte CipherKey, word ExpandedKey)
{
for (i = 0; i < Nk; i++)
ExpandedKey [i] = (CipherKey [4*i], CipherKey [4*i + 1], CipherKey [4*i + 2], CipherKey [4*i + 3]);
for (i = Nk; i<Nb* (Nr+1); i++)
{
temp = ExpandedKey [i - 1] ; if (i% Nk == 0)
temp = ByteSub (RotByte (temp)) ^Rcon [i/Nk] ; ExpandedKeyp] = ExpandedKey [i - Nk] ^temp;
}
}
Генерация ключа при Lk = 8:
KeyExpansion (byte CipherKey, word ExpandedKey)
{
for (i = 0; i < Nk; i++)
ExpandedKey [i] = (CipherKey [4*i], CipherKey [4*i + 1], CipherKey [4*i + 2], CipherKey [4*i + 3]);
for (i = Nk; i < Nb * (Nr + 1); i++)
{
temp = ExpandedKey [i - 1] ; if (i% Nk == 0)
temp = ByteSub (RotByte (temp)) ^Rcon [i/Nk] ; else if (i% Nk == 4)
temp = ByteSub (temp); ExpandedKey [i] = ExpandedKey [i - Nk] ^temp;
}
}
Раундовые функции:
Round (word State, word RoundKey)
{
ByteSub (State);
ShiftRow (State); MixColumn (State); AddRoundKey (State, RoundKey)
FinalRound (word State, word RoundKey) {
ByteSub (State);
ShiftRow (State);
AddRoundKey (State, RoundKey)
}
Полная процедура зашифрования блока текста:
Rijndael (byte State, byte CipherKey)
{
KeyExpansion (CipherKey, ExpandedKey);
AddRoundKey (State, ExpandedKey);
for (i = 1; i < Nr; i++)
Round (State, ExpandedKey + Nb*i);
FinalRound (State, ExpandedKey + Nb*Nr);
}
Раундовый ключ можно заготовить и вне функции Rijndael, a вместо ключа пользователя CipherKey использовать развертку ключей ExpandedKey. Преимущества такого варианта очевидны, когда для зашифрования текста длиной более одного блока нужно несколько раз вызывать функцию Rijndael с одним и тем же ключом пользователя.
Rijndael (byte State, byte ExpandedKey)
{
AddRoundKey (State, ExpandedKey);
for (i = 1; i < Nr; i++) Round (State, ExpandedKey + Nb*i);
FinalRound (State, ExpandedKey + Nb*Nr);
}
Для 32-разрядных процессоров раундовое преобразование лучше вычислять заранее и хранить результаты в виде таблиц. Заменяя операции перестановки и умножения на матрицу обращением к таблице, мы значительно сокращаем время работы как при зашифровании, так и (как будет видно позже) при расшифровании. С помощью таблиц вида

каждая из которых содержит по 256 четырехбайтовых слов (здесь w = 0,...,255; S (w) - S-блок подстановки), преобразование блока ![]() j = 0,..., Lb - 1, можно быстро выполнить как
j = 0,..., Lb - 1, можно быстро выполнить как
![]() ,
,
где ![]() (см. ShiftRow) и
(см. ShiftRow) и ![]() - j-й столбец раундового ключа.
- j-й столбец раундового ключа.
На последнем раунде преобразование MixColumn не выполняется, поэтому результат получается как
![]()
Конечно, можно воспользоваться таблицей из 256 четырехбайтовых слов, тогда
![]()
где r (a,b,c,d) = (d,a,b, с) - циклический сдвиг вправо на один байт.д.ля приложений с ограниченной памятью этот вариант чрезвычайно удобен, немного увеличится лишь время вычислений, необходимое для выполнения трех сдвигов.
2.7 РАСШИФРОВАНИЕПри расшифровании алгоритмом Rijndael процесс зашифрования выполняется в обратном порядке с обратными преобразованиями. Вот эти обратные функции:
InvFinalRound (word State, word RoundKey)
{
AddRoundKey (State, RoundKey);
InvShiftRow (State);
InvByteSub (State);
}
InvRound (word State, word RoundKey)
{
AddRoundKey (State, RoundKey);
InvMixColumn (State);
InvShiftRow (State);
InvByteSub (State);
}
Полная процедура расшифрования выглядит следующим образом:
InvRijndael (byte State, byte CipherKey)
{
KeyExpansion (CipherKey, ExpandedKey);
InvFinalRound (State, ExpandedKey + Nb*Nr);
for (i = Nr - 1; i > 0; i--)
InvRound (State, ExpandedKey + Nb*i);
AddRoundKey (State, ExpandedKey);
}
Алгебраическая структура алгоритма Rijndael позволяет упорядочить преобразования зашифрования так, что и для них можно будет использовать таблицы. Заметим, что подстановка S и преобразование ShiftRow коммутируют, поэтому внутри одного раунда их можно поменять местами. Благодаря свойству гомоморфизма ![]() линейных преобразований, операции InvMixColumn и сложение с раундовым ключом можно тоже поменять местами. В пределах одного раунда это выглядит так:
линейных преобразований, операции InvMixColumn и сложение с раундовым ключом можно тоже поменять местами. В пределах одного раунда это выглядит так:
InvFinalRound (word State, word RoundKey)
{
AddRoundKey (State, RoundKey);
InvByteSub (State);
InvShiftRow (State);
}
InvRound (word State, word RoundKey)
{
InvMixColumn (State);
AddRoundKey (State, InvMixColumn (RoundKey));
InvByteSub (State);
InvShiftRow (State);
}
Если порядок функций не менять, то их можно переопределить:
AddRoundKey (State, RoundKey);
InvRound (word State, word RoundKey)
{
InvByteSub (State);
InvShiftRow (State);
InvMixColumn (State);
AddRoundKey (State, InvMixColumn (RoundKey));
}
InvFinalRound (word State, word RoundKey)
{
InvByteSub (State);
InvShiftRow (State);
AddRoundKey (State, RoundKey);
}
Отсюда получаем структуру, аналогичную зашифрованию. Из соображений эффективности в процедуре lnvRound () отложим применение функции InvMixColumn к раундовому ключу до вычисления развертки, в которой первый и последний раундовые ключи из InvMixColumn оставим без изменений. "Обратные" раундовые ключи генерируются процедурой
InvKeyExpansion (byte CipherKey, word InvEpandedKey)
{
KeyExpansion (CipherKey, InvExpandedKey);
for (i = 1; i < Nr; i++)
InvMixColumn (InvExpandedKey + Nb*i);
}
Теперь полная процедура расшифрования выглядит так:
InvRijndael (byte State, byte CipherKey)
{
InvKeyExpansion (CipherKey, InvExpandedKey);
AddRoundKey (State, InvExpandedKey + Nb*Nr);
for (i = Nr-1; i>0; i--)
InvRound (State, InvExpandedKey + Nb*i);
InvFinalRound (State, InvExpandedKey);
}
По аналогии с зашифрованием можно и для расшифрования составить таблицы предвычислений. С помощью следующих преобразований:
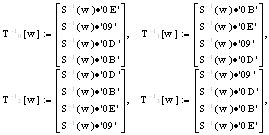
(где w = 0,...,255; S-1 (w) - обратный S-блок подстановки) получаем результат обратного раундового преобразования блока ![]() j = 0,..., Lb - 1:
j = 0,..., Lb - 1:
![]() ,
,
где ![]() и
и ![]() - j-й столбец "обратного" раундового ключа.
- j-й столбец "обратного" раундового ключа.
Здесь на последнем раунде тоже не выполняется преобразование MixColumn, и результатом последнего раунда будет
![]() ,
,
где j = 0,…,Lb -1.
Для экономии памяти для расшифрования также можно составить таблицу всего из 256 четырехбайтовых слов, в которой
![]() ,
,
где r (а,b,c,d) = (d,a,b, с) - циклический сдвиг вправо на один байт.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. М. Вельшенбах. Криптография на Си и С++ в действии. М.: ТРИУМФ, 2004.
2. М. Яхтсмен. Теория и практика информационной безопасности. Под редакцией Зегжды П.Д. 1996.
3. Методы и средства защиты компьютерной информации. Методические указания к лабораторным работам для студентов специальности 220100 - Вычислительные машины, комплексы, системы и сети и направления 552800 - Информатика и вычислительная техника Сост.С. С. Соколов.
Похожие работы
... оборудования. Существуют программно-аппаратные средства обеспечивающее блокировку доступа к файлу с секретной информацией а также уничтожение той программы, которая обеспечивает несанкционированный запрос к данному файлу Криптографические методы защиты данных Криптографические методы защиты данных — это методы защиты данных с помощью криптографического преобразования, под которым ...
... оптимальный момент для возбуждения дела, а также определить характер и последовательность первоначальных следственных действий, организационных и иных мероприятий. Успех расследования преступления в сфере компьютерной информации во многом обеспечивают: быстрота и решительность действий следователя и оперативного сотрудника в самые первые часы производства по делу; организованное взаимодействие с ...
... техники: машинными носителями: аппаратурой и приспособлениями он располагал: где: на какие средства их приобрел и где хранил?" [6] 3? РАССЛЕДОВАНИЕ ПРЕСТУПЛЕНИЙ В СФЕРЕ КОМПЬЮТЕРНОЙ ИНФОРМАЦИИ? 3?1? Расследование неправомерного доступа к компьютерной информации Согласно ст? 272 УК ответственность за деяние наступает при условии: если неправомерный доступ к компьютерной информации ...
... 1997 г., восполнили существенный пробел в защите одного из важнейших продуктов человеческой деятельности, впервые выделив в рамках IX раздела самостоятельную главу, именуемую “Преступления в сфере компьютерной информации”. Главу открывает ст. 272 УК РФ, предусматривающая ответственность за неправомерный доступ к охраняемой законом компьютерной информации, т. е. информации на машинном носителе в ...
0 комментариев