Навигация
Установка значения весовых коэффициентов и переход к этапу 4
6. Установка значения весовых коэффициентов и переход к этапу 4.
Построим область допустимых решений задачи (рис.5) и линии уровня, определяемые целевой функцией (11):
j (X) = - 2x1 + 8x2 - x12 - x22
j (X) = - (x12 + 2х1 + 1) + 1 - (x22 - 8х2 + 16) + 16
j (X) = - (x1 + 1) 2 + 1 - (x2 - 4) 2 + 16
j (X) = - (x1 + 1) 2 - (x2 - 4) 2 + 17 (13)
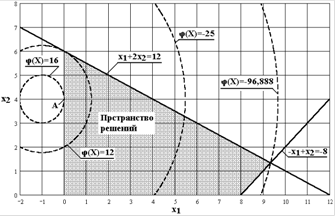
Рис.5. Область допустимых решений
Линиями уровня служат окружности с центром в точке (- 1;
4). Точка касания одной из этих окружностей с областью допустимых решений и является искомой точкой максимального значения целевой функции.
Из вида целевой функции (11) можно сделать вывод:
чем дальше точка от центра окружности, тем всё меньше целевая функция, максимум целевой функции будет в точке касания окружности вертикальной оси координат (точка А на рис.5), при этом: х1 = 0; х2 = 4
и целевая функция равна:
j (X) = - (x1 + 1) 2 - (x2 - 4) 2 + 17 = - (0 + 1) 2 - (4 - 4) 2 + 17 = 16.
Для решения задачи методом штрафных функций примем начальное значение допустимого решения:
![]() .
.
Выбираем шаг вычислений и точность вычислений:
![]() и
и ![]() .
.
Принимаем весовые коэффициенты:
![]() ,
,
![]() .
.
Находим частные производные от целевой функции:
![]() ,
,
![]() .
.
Определяем частные производные от функций ограничения:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Далее вычисления производим в среде MS Excel (см. файл KursR_MMPR. xls) по алгоритму, приведённому на Рис.6.
Результат расчёта в среде MS Excel представлен в таблице 1.
Графически решение представлено на рис.5, где максимальное значение целевой функции достигается в точке А (0;
4) и равно:
j (X) = 16.
Ответ:
В точке
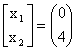
имеем глобальный максимум целевой функции:
j (X) = 16.
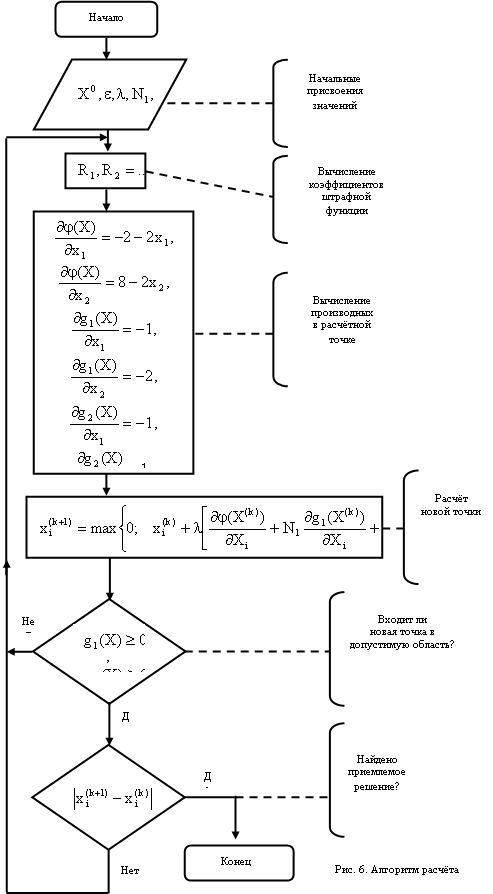
Таблица 1. Результат расчёта в среде MS Excel
| № итерации | Текущее | Допустимое решение? |
|
|
|
|
|
|
|
| Новое | Допустимое решение? | Конец расчёта? | ||
|
|
|
|
| ||||||||||||
| 1 | 3 | 2 | Да | 0 | 0 | -8 | 4 | -1 | -2 | -1 | 1 | 2,2 | 2,4 | Да | Нет |
| 2 | 2,2 | 2,4 | Да | 0 | 0 | -6,4 | 3,2 | -1 | -2 | -1 | 1 | 1,56 | 2,72 | Да | Нет |
| 3 | 1,56 | 2,72 | Да | 0 | 0 | -5,12 | 2,56 | -1 | -2 | -1 | 1 | 1,048 | 2,976 | Да | Нет |
| 4 | 1,048 | 2,976 | Да | 0 | 0 | -4,096 | 2,048 | -1 | -2 | -1 | 1 | 0,6384 | 3,1808 | Да | Нет |
| 5 | 0,6384 | 3,1808 | Да | 0 | 0 | -3,2768 | 1,6384 | -1 | -2 | -1 | 1 | 0,31072 | 3,34464 | Да | Нет |
| 6 | 0,31072 | 3,34464 | Да | 0 | 0 | -2,62144 | 1,31072 | -1 | -2 | -1 | 1 | 0,048576 | 3,475712 | Да | Нет |
| 7 | 0,048576 | 3,475712 | Да | 0 | 0 | -2,09715 | 1,048576 | -1 | -2 | -1 | 1 | 0 | 3,58057 | Да | Нет |
| 8 | 0 | 3,58057 | Да | 0 | 0 | -2 | 0,838861 | -1 | -2 | -1 | 1 | 0 | 3,664456 | Да | Нет |
| 9 | 0 | 3,664456 | Да | 0 | 0 | -2 | 0,671089 | -1 | -2 | -1 | 1 | 0 | 3,731565 | Да | Нет |
| 10 | 0 | 3,731565 | Да | 0 | 0 | -2 | 0,536871 | -1 | -2 | -1 | 1 | 0 | 3,785252 | Да | Нет |
| 11 | 0 | 3,785252 | Да | 0 | 0 | -2 | 0,429497 | -1 | -2 | -1 | 1 | 0 | 3,828201 | Да | Нет |
| 12 | 0 | 3,828201 | Да | 0 | 0 | -2 | 0,343597 | -1 | -2 | -1 | 1 | 0 | 3,862561 | Да | Нет |
| 13 | 0 | 3,862561 | Да | 0 | 0 | -2 | 0,274878 | -1 | -2 | -1 | 1 | 0 | 3,890049 | Да | Нет |
| 14 | 0 | 3,890049 | Да | 0 | 0 | -2 | 0,219902 | -1 | -2 | -1 | 1 | 0 | 3,912039 | Да | Нет |
| 15 | 0 | 3,912039 | Да | 0 | 0 | -2 | 0,175922 | -1 | -2 | -1 | 1 | 0 | 3,929631 | Да | Нет |
| 16 | 0 | 3,929631 | Да | 0 | 0 | -2 | 0,140737 | -1 | -2 | -1 | 1 | 0 | 3,943705 | Да | Нет |
| 17 | 0 | 3,943705 | Да | 0 | 0 | -2 | 0,11259 | -1 | -2 | -1 | 1 | 0 | 3,954964 | Да | Нет |
| 18 | 0 | 3,954964 | Да | 0 | 0 | -2 | 0,090072 | -1 | -2 | -1 | 1 | 0 | 3,963971 | Да | Да |
Литература
1. Таха Х. Введение в исследование операций, 7-е издание: Пер с англ. - М.: Изд. дом "Вильямс", 2005.
2. Реклейтис Г., Рэйвиндран А., Рэгсдел К. Оптимизация в технике / Пер. с англ. В 2-х кн. Кн.1 - М: Мир, 1986.; Кн.2 - М: Мир, 1986.
3. Акулич И.Л. Математическое программирование в примерах и задачах: Учебное пособие. - М.: Высшая школа, 1986.
Похожие работы
... себя почти все методы оценки издержек и экономических выгод, а также относительной рентабельности деятельности предприятия. Типичная «экономическая» модель основана на анализе безубыточности, методе принятия решений с определением точки, в которой общий доход уравнивается с суммарными издержками, т.е. точки, в которой предприятие становится прибыльным. Эти модели широко применяются в бухгалтерском ...
... и использования специалистов-пpофессионалов по анализу ваpиантов пpинимаемых pешений; pазpаботки и пpактического использования специальных методов анализа и сpавнения сложных альтеpнатив, возникающих в пpоцессе выбоpа. 3.ОБЩИЕ ПОДОХДЫ И РАЦИОHАЛЬHЫЕ ПРОЦЕДУРЫ В ПРОБЛЕМАХ ВЫБОРА В последние 20-30 лет появились подходы, pассматpиваемые многими как унивеpсальное сpедство pешения всех ...
... эффективности инвестиций - ARR (Accounted Rate of Return). 2 Постановка задачи Целью данной курсовой работы является сравнительная характеристика методов принятия решения относительно инвестиционных программ. В работе рассматриваются три инвестиционные альтернативы. Расчетная процентная ставка равна 10% (i = 0.1). Критерием оценки является критерий максимизации капитализированной стоимости ...
, как «риск», «определенность», «неопределенность». Будут рассмотрены некоторые примеры принятия решений в условиях определенности, риска и неопределенности. Также будут рассмотрены некоторые методы и модели принятия решений. В нашей стране долгое время проблеме обучения управленческого персонала не уделялось должного внимания. Это происходило потому, что в административно-командной системе ...

0 комментариев