Моделирование информацийных потоков

МІНІСТЕРСТВО ОСВІТИ ТА НАУКИ УКРАЇНИ КИЇВСЬКА ДЕРЖАВНА АКАДЕМІЯ ВОДНОГО ТРАНСПОРТУ імені гетьмана Петра-Конашевича Сагайдачного КОНТРОЛЬНА РОБОТА З ДИСЦИПЛІНИ “ Моделювання інформаційних потоків ”

студента 5 курсу

заочного відділення спеціальності

“Менеджмент організацій”

К И Ї В - 2 0 0 6

1. Сортировка вставками

Пусть надо упорядочить N элементов R1, R2…Rn.

Назовем их записями, а всю совокупность N назовем файлом. Каждая запись Rj имеет свой ключ Kj, который и управляет процессом сортировки. Помимо ключа, запись может содержать дополнительную «сопутствующую информацию», которая не влияет на сортировку, но всегда остается в этой записи.

Отношение порядка « < » на множестве ключей т.о., чтобы для всех 3-х значений ключей а, в, с выполнялись следующие условия:

1)    справедливо одно и только одно из соотношений: а< b, a=b, b<a (закон Трихотомии);

2)    если а< b и b<с, то а<с (закон Транзит-ти).

Эти 2 свойства определяют математическое понятие линейного упорядочения, которое называют еще совершенным упорядочением. Любое множество с отношением « < », удовлетворяемых свойствам 1) и 2), поддается сортировке большинством методом сортировки, который мы будем рассматривать, хотя некоторые из них годятся только для числовых и буквенных ключей с обычным отношением порядка.

Задача сортировки - найти такую перестановку записей p(1), p(2), p(n) после К ключи расположились бы в неубывающем порядке:

Kp(1)<Kp(2)<...<Kp(n)

Сортировка называется устойчивой, если она удовлетворяет дополнительному условию, что записи с одинаковыми ключами остаются в прежнего порядке, то есть:

Р(i)<Р(j), если Kp(i)=Kp(j) и i<j

Обычно сортировку подразделяют на 2 класса:

•     внутреннюю, если записи, которые сортируются, находятся в операционной памяти;

•     внешнюю, если некоторые из записей, которые сортируются, находятся во вспомогательной памяти.

Ограничим наше рассмотрение лишь внутренними сортировками. Алгоритмы сортировки можно подразделить на несколько групп:

A. Сортировка вставками. Элементы просматриваются по одному, и каждый новый
элемент вставляется в подходящее место среди ранее упорядоченных элементов.

B. Обменная сортировка. Если два элемента расположены не по порядку, то они
меняются местами. Этот процесс повторяется до тех пор, пока элементы не будут упорядочены.

C. Сортировка посредством выбора. Сначала выделяется наименьший (или, может быть,
наибольший) элемент и каким-либо- образом отделяется от остальных, затем выбирается
наименьший (наибольший) из оставшихся и так далее.

Д. Сортировка подсчетом. Каждый элемент сравнивается со всеми остальными, окончательное положение элемента определяется подсчетом числа наименьших ключей.

Е. Специальная сортировка, которая хороша для нескольких элементов, но не поддается простому обобщению на случай большего числа элементов.

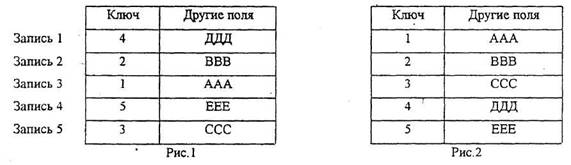
Сортировка выполняется или над самими записями, или над указателями некоторой вспомогательной таблицы, например, рассматриваем рис.1, на котором представлен файл с 5 записями. Если этот файл отсортировать в возрастающем порядке по указанному числовому ключу, то результирующий файл будет таким, как показано на рис.2. В этом случае были отсортированы и сами записи.

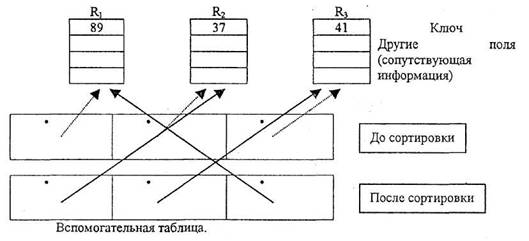
Если записи и/или ключи занимают несколько слов памяти, то часто лучше составить новую таблицу адресов (ссылок), которые указывают на записи и работают с этими адресами, не перемещая громоздкие записи. Такой метод называется сортировкой таблицы адресов.

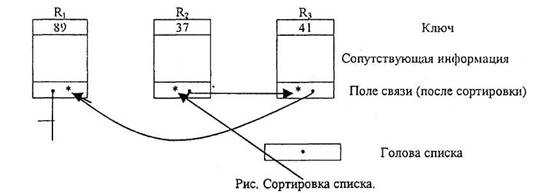
Если ключи короткие, а сопутствующая информация в записях велика, то для повышения скорости ключи можно вынести в таблицу адресов; это называется сортировкой ключей. Другие схемы сортировки используют вспомогательное поле связи, которое включается в каждую запись. Связи обрабатываются т.о., что в результате все записи оказываются связанными в линейный список, в котором каждая связь указывает на следующую по порядку запись. Это называется сортировкой списка.

Достаточно хороший алгоритм затрачивает на сортировку N записей время порядка NlogN; при этом требуется около log N «проходов» по данным.

При N--»oo время работает на N (log)² , если все ключи различны, так как и размеры ключей увеличиваются с ростом N, но практически N всегда остается ограниченным.

Сортировка вставками.

Простые вставки. Пусть 1 < j < N и записи R1,..., Rj-1 уже размещены так, что К1 < К₂ < ... Kj1

Будем сравнивать по очереди Kj с Kj-1 Kj-2_> ... до тех пор, пока не обнаружим, что запись Rj следует вставить в R1 и R1+i; тогда подвинем записи Ri+1, ..., Rj-1 на одно место вверх и поместим новую запись в позицию i+1. Удобно совмещать операции сравнения и перемещения, перемежая их друг с другом. Поскольку запись Rj как бы «проникает на положенный ей уровень», этот способ часто называют просеиванием или погружением.

Алгоритм (Сортировка простыми вставками). Записи R₁...,R_N переразмещаются на том же месте; после завершения сортировки их ключи будут упорядочены: К1 < ... < K_N.

Шаг 1 [Цикл по j]. Выполнить шаги 2-5 при j=2,3,...,N и после этого завершить алгоритм.

Шаг 2 [Установить i, К, R]. Установить i=j-l, K=Kj, R=Rj. (В последующих шагах мы попытаемся вставить запись R в нужное место, сравнивая К с Кi при убывающих значениях i).

Шаг 3 Сравнить К, K1. Если К > Ki, то перейти к шагу 5 (Мы нашли искомое место для записи R).

Сортировка простыми вставками.

98 12 13 7 3 21 99 128

j=2 K₂=

i=l K=12 R=R₂

R₂=R1 i=0

12 98 13 7 3 21 99 128

j=3

i=2 K=K₃=13 R=R₃ R₃=R₂ i=2

12 13 98 7 3 2199 128

j=4

i=3 K=K4=7 R=R4 R4=R₃ i=3

12 13 7 98

j=2

i=l K=K₂=13 R=R₂

12 13 7 98

j=3

i=2 K=K₃=7 R=R₃ R₃=R₂ i=2

12 7 13 98

j=4

i=3 K=K4=98 R=R4

12 7 13 98

j=2

i=l K=K₂=7 R=R₂ R₂=R1 i=0

7 12 13 98

j=3

i=2 K=K₃=13 R=R₃

7 12 13 98

j=4

i=3 K=K4=98 R=R4

7 12 13 98

10 просмотров.

Шаг 4 [Переместить Ri, уменьшить i]. Установить Ri+1=Ri, i =i-l. Если i>0, то вернуться к шагу 3. (Если i=0, то К - наименьший из рассмотренных до сих пор ключей, а значит, запись R должна занять первую позицию).

Шаг 5 [R на место Ri+1]. Установить Rj+1= R