Министерство науки и образования Украины
Харьковский Национальный Университет им. В.Н.Каразина
Факультет компьютерных наук
Кафедра моделирования систем и технологий
Моделирование логнормального распределения
Курсовая работа по дисциплине
«Компьютерное моделирование стохастических процессов»
Исполнитель *************
студент ****
Руководитель
Ст. преп. ************
Харьков 2007
План
1. Введение
2. Логнормальное распределение
3. Применение логнормального распределения
4. Постановка задачи
5. Реализация поставленной задачи
6. Инструкция пользователю
7. Описание программного модуля
8. Заключение
9. Список используемой литературы
10. Общие данные логнормального распределения
Введение
Данная работа была создана с целью промоделировать логнормальное распределение. Проект представляет собой программный продукт, который генерирует случайные величины распределенные по вышеуказанному закону, отображает теоретическую плотностью распределения и плотность полученную в результате эксперимента. Также считается мат. ожидание и дисперсия теоретически и экспериментально.
Логнормальное распределение
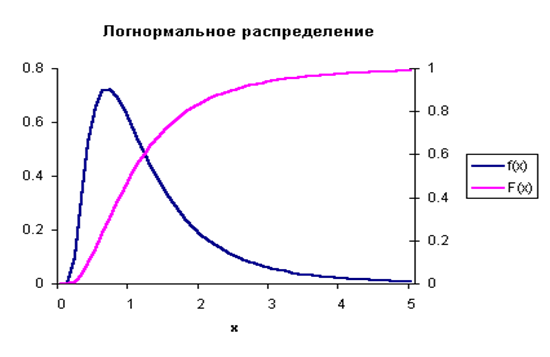
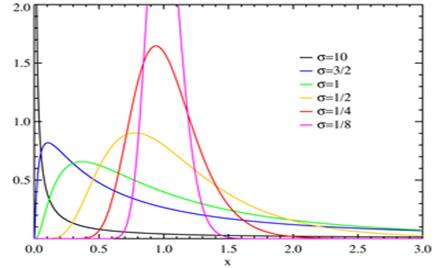
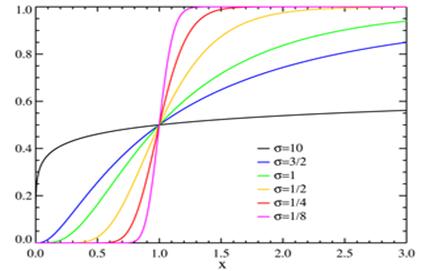
Случайная величина X имеет логнормальное распределение с параметрами μ, σ, если X = exp(Y), где Y имеет нормальное распределение с параметрами μ, σ. Случайная величина с логнормальным распределением является непрерывной, и принимает только положительные значения. Графики плотности (привязан к левой вертикальной оси ординат) и функции (привязан к правой оси ординат) логнормального распределения с параметрами μ = 0, σ = 0.7 приведен на следующем рисунке.
Характеристики
В следующей таблице приведены формулы для вычисления характеристик логнормального распределения.
Плотность распределения 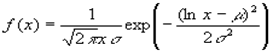
Функция распределения* ![]()
Математическое ожидание ![]()
Стандартное отклонение ![]()
Дисперсия ![]()
Асимметрия ![]()
Мода ![]()
* Функция логнормального распределения F через элементарные функции не выражается. Для приближенного вычисления функции этого распределения с параметрами μ, σ можно воспользоваться формулой F(x) = Φμ,σ(ln x), где Φμ,σ - функция нормального распределения с параметрами μ, σ.
Моделирование
Моделирование значений случайной величины с логнормальным распределением (с параметрами μ, σ) проводится по формуле X = exp(Y), где Y имеет нормальное распределение с теми же параметрами..
Применение логнормального распределения
В статистике так называемое логнормальное распределение применяется в том случае, когда начинает изменяться цена актива в будущем – а это случайный процесс, который в принципе должен описываться нормальным распределением. В то же время для целей вероятностной оценки стоимости актива в теории пользуются не нормальным, а логнормальным распределением. Это обусловлено следующими причинами. Во-первых, нормальное распределение симметрично относительно ее центральной оси и может иметь как положительные, так и отрицательные значения; однако цена актива не может быть отрицательной. Во-вторых, нормальное распределение говорит о равной вероятности для значений переменной отклониться вверх или вниз. В то же время на практике, например, имеет место инфляция, которая оказывает давление на цены в сторону их повышения, а также сама временная сущность денег: стоимость денег сегодня меньше, чем стоимость денег вчера, но больше, чем стоимость денег завтра. Кривая логнормального распределения всегда положительна и имеет правостороннюю скошенность (асимметрично), т.е. она указывает на большую вероятность цены отклониться вверх. Поэтому если, допустим, цена актива составляет 50 долл., то кривая логнормального распределения свидетельствует о том, что опцион пут с ценой исполнения 45 долл. должен стоить меньше опциона колл с ценой исполнения 55 долл., в то время как в соответствии с нормальным распределением они должны были бы иметь одинаковую цену. Хотя нельзя надеяться, что приведенные исходные предположения в точности выполняются во всех реальных рыночных ситуациях, тем не менее принято считать, что логнормальное распределение достаточно хорошо как первое приближение в случае активов, которыми торгуют на конкурентных рынках аукционного типа для длинных рассматриваемых периодов.
Постановка задачиБыла поставлена задача промоделировать логнормального распределения, вывести график плотности распределения, полученный при помощи аналитических расчетов, и график, промоделированный с помощью стохастического метода. Посчитать математическое ожидание и дисперсию аналитическим и стохастическим способами и занести полученные результаты в таблицу (SrtingGrid).
Реализация поставленной задачи
Для решения поставленной я использовал среду программирования Delphi 7.
Сначала были сделаны расчеты по формулам которые описывались выше для того, чтобы отобразить график плотности логнормального распределения при помощи аналитических расчетов.
Для того, чтобы получить график плотности распределения на основе стохастических преобразований, был выбран метод Неймана.
Также нужно было посчитать математическое ожидание и дисперсию и ввести полученные результаты на экран. Формулы которых представлены ниже
| Математическое ожидание |
|
| Дисперсия |
|
var
Form1: TForm1;
kk:Int64;
flag:boolean;
implementation
Плотность распределения
function TForm1.PL(x:double):double; //--density of distribution
begin
if x<>0 then
result := exp(-(ln(x)-mu)*(ln(x)-mu)/(2*sigma*sigma))/(x*sigma*Sqrt(2*Pi))
else
result := 0;
end;
function TForm1.LogNorm() : double; //--for a method of Neumann
var
y : real;
x : double;
begin
repeat
x := a+random*(b-a);
f := PL(x);
y := fmax*random;
until y<f;
result := x;
end;
procedure TForm1.Clear; //------------clear array---------
const M=50;
var j : integer;
begin
for j:=0 to (M-1) do
begin
gist[j] := 0;
end;
end;
procedure TForm1.Panel1Click(Sender: TObject);
var
x, r, sr, h1, h2, Ob,g1,g2, chi2_N, chi2_12, chi2_if, sum, Z : double;
p, y, Mat, Mat2, Disp : real;
M, j : integer;
N, i, u : longint;
begin
flag:=false;
Gauge1.Progress:=0;
//-------**All fields must be filled!**---------
if (E1.Text='') or (E2.Text='') or (E3.Text='') or (E4.Text='') or
(E5.Text='') then
begin
with Application do
begin
NormalizeTopMosts;
MessageBox('All of fields must be filled!', 'Error', MB_OK);
RestoreTopMosts;
end;
exit;
end;
//----------**initialization**--------------
T := GetTime;
Clear;
Chart1.Series[0].Clear;
Chart1.Series[1].Clear;
Chart1.Series[2].Clear;
sigma := StrToFloat(E1.Text);
mu := StrToFloat(E2.Text);
a := StrToFloat(E3.Text);
b := StrToFloat(E4.Text);
kk:=StrToint64(E5.Text);
if kk>2000000000 then
begin
Showmessage ('Очень большое число, введите меньшее');
exit;
end;
N := StrToInt(E5.Text);
g1:=100/N;
g2:=0;
Randomize;
M := 50;
//---------------**theoretical method**------------------
for i:=1 to 100 do
begin
if (i mod 10) =0 then application.ProcessMessages;
x := a+i*(b-a)/100;
//p := PL(x);
if x<>0 then
p := exp(-(ln(x)-mu)*(ln(x)-mu)/(2*sigma*sigma))/(x*sigma*Sqrt(2*Pi))
else
p := 0;
Chart1.Series[0].AddXY(x, p);
end; //---theoretical
//***********************************************************
Метод Неймана
//---------------**method of Neumann**------------------------
fmax :=Chart1.Series[0].MaxYValue;
{for i:=1 to N do
begin
if (i mod 10) =0 then application.ProcessMessages;
x := a+i*(b-a)/N;
f := PL(x);
if (f>fmax)then
fmax := f;
end;} //max
//------------------------------
Clear;
chi2_N:=0;
Mat:=0;
Mat2:=0;
Disp:=0;
i:=0;
Clear;
chi2_if := 0;
while true do
begin
if (i mod 10) =0 then application.ProcessMessages;
inc(i);
x := LogNorm();
Mat := Mat+x; //expectation
Mat2 := Mat2 +sqr(x);
if (x>b) or (x<a) then
continue;
u := trunc((x-a)/((b-a)/M));
gist[u] := gist[u]+1;
h1 := random;
h2 := random;
Ob := sqrt(-2*ln(h1))*cos(2*Pi*h2);
Ob := mu+Ob*sigma;
x := exp(Ob);
if (x>b) or (x<a) then
continue;
u := trunc((x-a)/((b-a)/M));
gist1[u] := gist1[u]+1;
g2:=g2+g1;
Gauge1.Progress:=trunc(g2)+1;
if i>N then break;
if flag=true then
begin
N:=i;
break;
end;
end;
Mat := Mat/N;
Mat2 := Mat2/N;
Disp := Mat2 - sqr(Mat);
for j:=0 to (M-1) do //------histogram
begin
sum := (Power(N*PL(a+(b-a)/M*(j+0.5))*(b-a)/M-gist[j], 2))/
(N*PL(a+(b-a)/M*(j+0.5))*(b-a)/M);
chi2_N := chi2_N+sum;
Chart1.Series[1].AddXY((a+(j+0.5)*(b-a)/M), gist[j]/N*M/(b-a));
end;
E6.Text := FloatToStrF(chi2_N, fffixed, 4, 4);//--chi-square for a Neumann
//****************************************************************
Метод обратной функции
//--------------**method of inverse function**-----------------
Clear;
chi2_if := 0;
{for i:=1 to N do
begin
h1 := random;
h2 := random;
Ob := sqrt(-2*ln(h1))*cos(2*Pi*h2);
Ob := mu+Ob*sigma;
x := exp(Ob);
if (x>b) or (x<a) then
continue;
u := trunc((x-a)/((b-a)/M));
gist[u] := gist[u]+1;
end;}
for j:=0 to (M-1) do //------histogram
begin
sum := (Power(N*PL(a+(b-a)/M*(j+0.5))*(b-a)/M-gist1[j], 2))/
(N*PL(a+(b-a)/M*(j+0.5))*(b-a)/M);
chi2_if := chi2_if+sum;
Chart1.Series[2].AddXY((a+(j+0.5)*(b-a)/M), gist1[j]/N*M/(b-a));
gist1[j]:=0;
end;
E8.Text := FloatToStrF(chi2_if, fffixed, 4, 4); //chi-sq for a inverse function
E10.Text := FloatToStr(exp(mu+sqr(sigma)/2)); //--expectation (teor)
E11.Text := FloatToStr(Mat); //--expectation (experim)
E12.Text := FloatToStr((exp(sqr(sigma))-1)*exp(2*mu+sqr(sigma)));
E13.Text := FloatToStr(Disp);
D := GetTime;
Z := MilliSecondSpan(D, T);
e5.Text:=IntTostr(N);
Edit1.Text := FloatToStrF(Z, fffixed, 6, 6);
//*****************************************************************
end;
procedure TForm1.Panel7Click(Sender: TObject);
begin
Close;
end;
procedure TForm1.E1KeyPress(Sender: TObject; var Key: Char);
begin
if (key='-')
then begin
if Pos ('-', (Sender as TEdit).Text)=0 then Begin (Sender as TEdit).SelStart:=0; key:='-'; end
else key:=#0;
end;
if Sender is TEdit then
begin
if Not((Key in ['0'..'9'])or (Key=Chr(vk_Back))
or (Key=DecimalSeparator) or (Key='-')) then
Key:=#0
else
begin
if Key = DecimalSeparator then
if Pos(DecimalSeparator,(Sender as TEdit).Text)>0 then
Key:=#0;
end;
end;
end;
procedure TForm1.Aboutme1Click(Sender: TObject);
begin
AboutBox.Show;
end;
procedure TForm1.Timer1Timer(Sender: TObject);
begin
Panel19.Caption := TimeToStr(Time);
end;
procedure TForm1.E1KeyDown(Sender: TObject; var Key: Word;
Shift: TShiftState);
begin
if (ssShift in Shift)then
key:=0;
end;
procedure TForm1.Panel20Click(Sender: TObject);
begin
flag:=true;
end;
end.
Инструкция пользователюПри запуске программы перед пользователем открывается форма, на которой есть поля ввода параметров, поля вывода посчитанных значений, поле для вывода графика и кнопки, при нажатии на которые происходит то или иное событие.
Справа в разделе "Теоретически пользователь может ввести значение sigma и mu, те значения которые он считает нужными; a и b это интервал в пределах которого меняется график. И значение N – (количество єксперементов) – в зависемости от того сколько раз мы будем проводить єксперемент . В зависимости от выбора данных параметров пользователь может получить различные формы графика плотности вероятности.
В разделе "Критерий согласия" выводятся значения оценки Хи-квадрат для двух указанных методов. Ниже вывод математического ожидания и дисперсии, посчитанных теоретически и экспериментально.
Справа внизу формы выводится системное время и время выполнения расчётов в миллисекундах.
При нажатии на кнопку «Вывести графики и вычислить» слева выводятся график плотности логнормального распределения (построенный теоретически), гистограммы распределения случайной величины по логнормальному закону, смоделированные при помощи метода Неймана и метода обратной функции.
При нажатии на кнопку «Стоп» программа прекращаются свою работу и начинает считывать значения которые обработались до определенного момента и записует значения в поля.
При нажатии на кнопку «2D/3D» пользователь может наблюдать изменение графика из 2D в 3D и наоборот.
При нажатии на кнопку «Выход» программа будет завершена.
В закладке «About» пользователь может узнать о создателях данного программного продукта и краткое описание программного продукта.
Описание программного модуля.
Программа состоит из одного окна, на котором расположены все элементы управления. Справа формы находятся поля для ввода исходных данных.
В центре формы размещена кнопка «Вывести графики и вычислить», нажатие на которую запускает генератор случайных величин. На графике появляются две кривые описывающие функцию плотности логнормального распределения. Красным цветом изображена теоретическая кривая, а синим (метод обратной функции) и зеленым (метод Неймана) – полученная в результате эксперимента. Справа в полях отображаются значения математического ожидания и дисперсии..
Заключение
В моей работе я рассмотрел логнормальное распределение, мы получили графики плотности распределения и функции распределения, и связи с другими распределениями.
В результате работы был создан программный продукт в среде Delphi 7, где мы можем посмотреть как моделируется логнормальное распределение, выводятся графики плотности распределения при помощи аналитических расчетов и стохастических преобразований. А также вычисляется мат. ожидание и дисперсия, стохастическим и аналитическим способами.
Список используемой литературы
1. http://en.wikipedia.org
2. Шеффе Г. Дисперсионный анализ. - М.: Физматгиз, 1980. - 628 с.
3. «Delphi 2005: «Секреты программирования»», Михаил Фленов.
| Общие данные логнормальное распределение | |
| Плотность вероятности | |
| Функция распределения | |
| Параметры |
|
| Носитель |
|
| Плотность вероятности |
|
| Функция распределения |
|
| Математическое ожидание |
|
| Медиана | eμ |
| Мода |
|
| Дисперсия |
|
| Коэффициент асимметрии |
|
| Коэффициент эксцесса |
|
| Информационная энтропия |
|
Логнорма́льное распределе́ние в теории вероятностей - это двухпараметрическое семейство абсолютно непрерывных распределений. Если случайная величина имеет логнормальное распределение, то её логарифм имеет нормальное распределение.
Определение
Пусть распределение случайной величины X задаётся плотностью вероятности, имеющей вид:
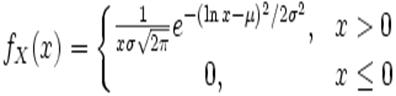 ,
,
где ![]() . Тогда говорят, что X имеет логнормальное распределение с параметрами μ и σ. Пишут: X˜LogN(μ,σ2).
. Тогда говорят, что X имеет логнормальное распределение с параметрами μ и σ. Пишут: X˜LogN(μ,σ2).
Формула для k-го момента логнормальной случайной величины X имеет вид:
![\mathbb{E}\left[X^k\right] = e^{k\mu + \frac{k^2\sigma^2}{2}},\; k \in \mathbb{N},](/images/referats/a44/132046/26.jpeg)
откуда в частности:
![]() ,
,
![\mathrm{D}[X] =\left(e^{\sigma^2}-1\right) e^{2\mu + \sigma^2}](/images/referats/a44/132046/28.jpeg) .
.
· Если ![]() - независимые логнормальные случайные величины, такие что
- независимые логнормальные случайные величины, такие что ![]() , то их произведение также логнормально:
, то их произведение также логнормально:
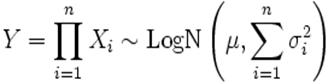 .
.
· Если X˜LogN(μ,σ2), то
Y = lnX˜N(μ,σ2).
Похожие работы
... . Под величиной риска принято понимать вероятность наступления того или иного нежелательного события, где под последним понимается событие, неблагоприятное для чистой текущей стоимости фирмы. К сожалению, к понятию финансового риска в полной мере применимо высказывание маршала Фоша о военном искусстве: сущность его довольно проста, но, к несчастью, его сложно претворить в жизнь. Обычно различают ...
... 66 ± 6 27 8 Заполнение жилищ 132 10 – 340 74 ± 6 34 9 Заполнение ям 43 20 – 141 51 ± 6 17 10 Вмещающие породы 180 7 – 209 25 ± 2 12 Таблица 1. Статистические характеристики магнитных свойств археологических объектов Значения стандарта s количественно характеризуют степень дисперсии (рассеяния) исследуемых параметров, которая по ряду объектов оказалась довольно высокой, что ...
... телегу впереди лошади – такая наука никуда не годится. Если рыночные прибыли подчиняются нормальному распределению, то имеется возможность развивать гипотезу и следствия из нее. В теории рынков капитала предположения о нормальности распределений и конечной дисперсии, так же как и основанные на них модели развивались вопреки эмпирической очевидности, которая всегда вступала в противоречие с ...
... сократилось на 15%. Относительно малое по сравнению с реально ощущаемым показанное снижение уровня жизни свидетельствует, на наш взгляд, прежде всего о том, что домашние хозяйства населения, адаптируясь к трудным условиям экономики выживания, сумели найти дополнительные трудовые и хозяйственные ресурсы для поддержания падающего уровня потребления. Правда, официальные данные не всегда согласуются с ...
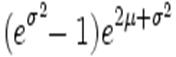
![\exp\left(-\left.\left[\frac{\ln(x)-\mu}{\sigma}\right]^2\right/2\right) \left/ \left(x\sigma\sqrt{2\pi}\right) \right.](/images/referats/a44/132046/16.jpeg)
![\frac{1}{2}+\frac{1}{2} \mathrm{Erf}\left[\frac{\ln(x)-\mu}{\sigma\sqrt{2}}\right]](/images/referats/a44/132046/17.jpeg)
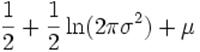
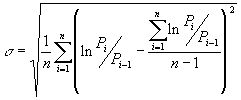
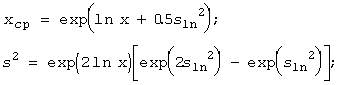


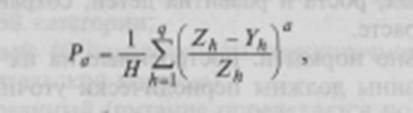
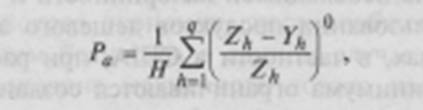
0 комментариев