Навигация
МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ
2. МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ
2.1 Описание модели АЦП
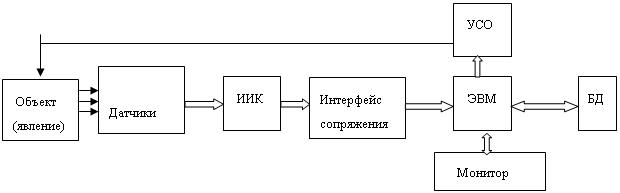
Одной из важнейших задач, решаемых автоматизированными системами, является сбор и обработка данных, поступающих от первичных преобразователей (датчиков), установленных на объектах автоматизации. Эти данные рассматривают как временные ряды.
Временной ряд - это множество наблюдений, генерируемых последовательно во времени. В зависимости от того, как изменяется время: непрерывно или дискретно, различают временные ряды непрерывные и дискретные.
Современные автоматизированные системы обрабатывают данные с помощью компьютеров, поэтому все данные, которые поступают в виде аналоговых сигналов, преобразуются в цифровую форму.
При исследовании процесса аналого-цифрового преобразования будут рассматриваться следующие временные ряды:
Х(t) - исходная физическая величина (непрерывный ряд);
х(t) - выходной сигнал датчика в вольтах, соответствующий функции Х(t) (непрерывный ряд);
С(t) - выход х(t) датчика, переведенный в непрерывные отсчёты (непрерывный ряд);
С(iT) - выход х(t) датчика, переведенный в непрерывные отсчёты, выполненные в дискретные моменты времени с периодом Т (дискретный ряд);
с(i) - выход х(t) датчика, переведенный в округленные отсчёты, полученные после операции квантования (дискретный временной ряд);
е(i) - погрешность, равная С(iT) - с(i).
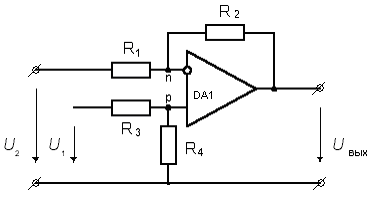
Фиктивный временной ряд С(t) введен здесь только для удобства. Как временной ряд С(t), так и ряд с(i) измеряются в одних единицах - отсчётах. Временной ряд С(t) есть просто результат линейного преобразования функции х(t) вида:
|
| (2.1) |
Например, если динамический диапазон изменения значений временного ряда х(t) на входе АЦП лежит в пределах от -5В до + 5В и ему соответствует интервал изменения значений временного ряда С(t) от 0 до 1023 на выходе (АЦП имеет 10 разрядов), то А = 102.3 (отсч/В) и В = 511.5 (отсч/В).
2.2 Спектральный анализ на основе преобразования Фурье
Дискретное преобразование Фурье (финитное) определяется следующим соотношением:
|
| (2.2) |
где X(k) - значение (комплексное) дискретного преобразования Фурье, определенное в частоте с номером k;
x(i) - значение (вещественное) исходного временного ряда, определенное в момент времени с номером i;
T - период дискретизации;
N - количество отсчетов (длина) временного ряда.
Дискретное преобразование Фурье связывает спектральную характеристику (комплексный спектр) X(k), определенную в дискретных значениях частоты (с номером k), с дискретными значениями временного ряда (сигнала) x(i), определенными в дискретные моменты времени (с номером i).
Точность представления спектральной характеристики определяется разрешением по частоте:
|
| (2.3) |
Обратное дискретное преобразование Фурье определяется следующим соотношением:
|
| (2.4) |
Из сравнения формул (2.2) и (2.4) следует, что они отличаются знаком показателя экспоненты, множителем перед знаком суммы, а также переменной суммирования. Это позволяет строить единые программы для прямого и обратного преобразований Фурье.
Применяя формулу Эйлера, выражение (2.2) можно привести к виду:
|
| (2.5) |
где
|
| (2.6) |
Оценивание спектральной плотности мощности (СПМ) с помощью дискретного преобразования Фурье осуществляется по формуле:
|
| (2.7) |
где X(k) - дискретное преобразование Фурье (спектральная характеристика) временного ряда ![]() , соответствующего процессу x(t), обладающего свойством эргодичности;
, соответствующего процессу x(t), обладающего свойством эргодичности;
T - период дискретизации процесса x(t);
N - длина временного ряда.
Черта в правой части формулы (2.7) означает операцию осреднения. Применение формулы (2.7) без операции осреднения приводит к получению "грубой" оценки СПМ. Формула (2.6) позволяет вычислить оценку СПМ посредством статистического осреднения модуля спектральной характеристики совокупности данных, поделенного на длину записи данных. Статистическое осреднение необходимо здесь потому, что ординаты спектральной характеристики являются случайными величинами, изменяющимися для каждой используемой реализации случайного временного ряда ![]() .
.
Операция осреднения уменьшает статистическую изменчивость, или повышает статистическую устойчивость. В спектральном анализе случайных временных рядов на статистическую устойчивость влияют два параметра - разрешение по частоте ![]() и длина записи
и длина записи ![]() .
.
Можно показать, что оценки ПСМ приближенно имеют распределение ![]() с n степенями свободы, где
с n степенями свободы, где ![]() . Более того, для достаточно больших n, например,
. Более того, для достаточно больших n, например, ![]() , распределение
, распределение ![]() аппроксимируется гауссовским (нормальным) распределением. В этом случае нормированное стандартное отклонение (стандартное отклонение, связанное с оцениваемой величиной, т.е. процентная ошибка, или, в статистической терминологии, "коэффициент разброса") определяется соотношением:
аппроксимируется гауссовским (нормальным) распределением. В этом случае нормированное стандартное отклонение (стандартное отклонение, связанное с оцениваемой величиной, т.е. процентная ошибка, или, в статистической терминологии, "коэффициент разброса") определяется соотношением:
|
| (2.8) |
Величину ![]() называют стандартной ошибкой. Если
называют стандартной ошибкой. Если ![]() , то
, то
![]() .
.
Результат означает, что вычисление оценки СПМ с использованием полной длины временного ряда имеет стандартную ошибку, равную 100%.
Если отрезок ![]() поделить на m участков, то в этом случае:
поделить на m участков, то в этом случае:
|
| (2.9) |
Подставляя полученный результат в (2.7), найдем:
|
| (2.10) |
Таким образом, для повышения точности оценивания СПМ необходимо исходный временной ряд длины N разбить на m участков длины Nу, вычислить для каждого i-го участка ![]() по формуле (1), а затем найти осредненную оценку по формуле:
по формуле (1), а затем найти осредненную оценку по формуле:
|
| (2.11) |
Следует иметь в виду, что разрешение по частоте в рассмотренном случае определяется из соотношения ![]() . Число степеней свободы для найденной оценки СПМ можно найти следующим образом:
. Число степеней свободы для найденной оценки СПМ можно найти следующим образом:
|
| (2.12) |
Следовательно, для повышения степеней свободы и, соответственно, статистической устойчивости оценок СПМ необходимо увеличивать число участков для осреднения.
Повышение числа степеней свободы можно достичь другим способом - осреднением по частотам.
Сглаженная оценка:
|
| (2.13) |
полученная осреднением ![]() - соседних оценок спектральной характеристики, имеет распределение
- соседних оценок спектральной характеристики, имеет распределение ![]() с числом степеней свободы, равным примерно 2l. Это следует из теории о сложении величин, имеющих распределение
с числом степеней свободы, равным примерно 2l. Это следует из теории о сложении величин, имеющих распределение ![]() .
.
Следует отметить, что разрешение по частоте в данном случае определится из соотношения:
|
| (2.14) |
Поскольку операция осреднения линейная, оценку СПМ можно найти, комбинируя осреднение по участкам с осреднением по частотам. При этом сначала выполняется осреднение по участкам, а затем - по частотам. При осреднении по m участкам с последующим осреднением ![]() соседних спектральных оценок в итоге получаются оценки, число степеней свободы которых равно
соседних спектральных оценок в итоге получаются оценки, число степеней свободы которых равно ![]() . Разрешение в этом случае равно
. Разрешение в этом случае равно ![]() .
.
Похожие работы
... ФУНКЦИИ 4.3 ТЕСТИРОВАНИЕ РАЗРАБОТАННОГО ПО 5 РУКОВОДСТВО ПОЛЬЗОВАТЕЛЯ ЗАКЛЮЧЕНИЕ БИБЛИОГРАФИЯ ПРИЛОЖЕНИЯ 1 ВВЕДЕНИЕ Целью курсового проекта является разработка технического и программного обеспечения автоматизированной системы научных исследований (АСНИ). АСНИ предназначена для спектрального анализа данных, поступающих от первичных преобразователей физических величин, характеризующих ...
... , доступная с нескольких сотен терминалов, расставленных по всей больнице или даже за ее пределами, на дому у врачей или кабинетах частнопрактикующих специалистов. 2.2 Недостатки Автоматизированные системы ведения истории болезни имеют и некоторые недостатки. Они требуют больших начальных вложений по сравнению с бумажными эквивалентами из-за высокой стоимости компьютеров, программного обеспечения ...
... чем перейти непосредственно к разработке пользовательского интерфейса (ПИ), определим основные требования, предъявляемые к разработке интерфейса пользователя. Разработка пользовательского интерфейса (ПИ) ведется параллельно разработке архитектуры Автоматизированной Системы Управления документооборотом и разработке баз данных в целом и в основном предшествует её имплементации. Процесс разработки ...
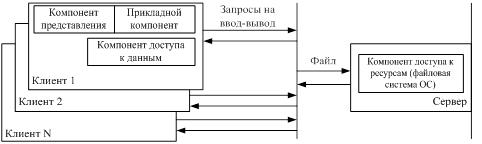
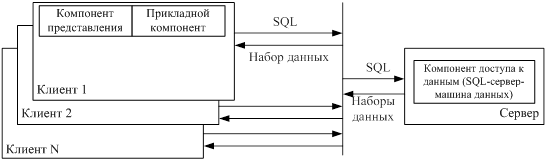
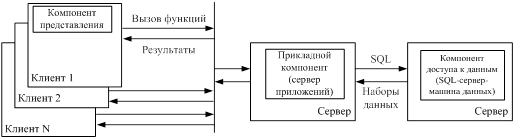
... называемые правила бизнеса) реализуются прикладными программами на клиентских установках (RDA-модель) или на сервере приложений (AS-модель). 2. Автоматизированные системы сбора, хранения и анализа информации Автоматизированные информационные системы (АИС) относятся к классу сложных систем, как правило, не столько в связи с большой физической размерностью, сколько в связи с многозначностью ...

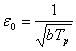
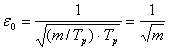
0 комментариев