Навигация
1.1.1. Сущность задачи
Оптимизация сетевого графика заключается в следующем: требуется при определенном количестве рабочих определить минимальное критическое время выпуска конечной продукции. В результате оптимальной расстановки трудовых ресурсов.
Задается общее количество этих самых ресурсов, в нашем случае – рабочих, занятых на рассматриваемом комплексе работ, а вместо продолжительности работ задаются по каждой работе необходимое число изделий подлежащих обработке.
Производительность труда всех рабочих одинакова. Продолжительность каждой работы обратно пропорциональна количеству рабочих, занятых на этой работе.
Важнейшие способы сокращения времени затрачиваемого на выполнения комплексов работ заключаются в следующем:
1) Прежде всего производится пересмотр топологии сети, т.е. изменения состава последовательности выполнения или взаимосвязи между работами. Такой пересмотр топологии сети возможен в том случае, когда для одних и тех же работ могут быть применены различные способы их выполнения или может быть изменена последовательность выполнения работ, в частности заменена последовательность параллельностью при выполнении отдельных работ.
В определенных случаях может обнаруживаться нецелесообразное использование ресурсов на многочисленных параллельных работах. Если параллельные работы выполняются рабочими одной специальности и квалификации при использовании определенных типов машин и механизмов, то целесообразно сделать так, чтобы те из работ, которые не лежат на критическом пути (и, следовательно, имеют резервы времени), выполнялись бы последовательно. Тогда часть ресурсов можно использовать для ускорения критических работ.
Используется также возможность более детального членения работ с тем, чтобы ускорить начало каких-либо критических работ.
2) Другим способом сокращения критического пути является переход от нормальных продолжительностей работ, находящихся на критическом пути, к минимально возможным, в первую очередь за счет перемещения ресурсов с работ, находящихся на некритических путях.
Перемещение ресурсов с некритических работ на критические должно, разумеется, производиться в разумных пределах, с тем, чтобы некритические работы сами не стали критическими.
3) В отдельных случаях для ускорения выполнения критических работ могут привлекаться дополнительные ресурсы со стороны.
Проведя тем или иным способом сокращение продолжительности работ на критическом пути, снова выполняют обработку сетевого графика, чтобы выявить достаточность принятых мер, а также узнать, не появились ли новые критические пути. Если новый вариант сети также не обеспечивает соблюдения директивных сроков выполнения всего комплекса работ, то вся процедура повторяется снова до тех пор, пока не будет получен удовлетворительный результат. Для сокращения количества пересчетов сетевого графика и его показателей проводят мероприятия по одновременному сокращению работ не только на критическом, но и на околокритических (т.е. близких к критическому) путях. Многократные пересчеты сетевого графика не являются обременительными и не занимают много времени и затрат труда специалистов, если все эти изменения осуществляются по специально разработанной документации и если все операции по перерасчету сетевого графика проводятся на ПЭВМ.
В отдельных случаях, особенно при жестких ограничениях в ресурсах, окончательным результатом расчетов по оптимизации сетевого графика может явиться обоснованное доказательство невозможности уложиться в заданный срок без устранения этих ограничений или пересмотра заданных технико-экономических характеристик. Это положение рассматривается соответствующими инстанциями, имеющими право решать указанные вопросы.
После того как определена продолжительность всего комплекса работ, осуществляется привязка всей сети к календарной шкале времени. В результате создается директивный документ – план-график проведения работ. В нем указываются даты начала и окончания каждой работы, а также величины резервов времени.
Директивный план-график рассылается ответственным исполнителям, после чего начинается выполнение комплекса работ в соответствии с разработанным графиком.
Однако нередко возникает необходимость, прежде чем приступить к работам, проверить распределение ресурсов по календарным срокам выполнения работ. Дело в том, что, определяя продолжительность выполнения той или иной работы, включенной в сетевой график, мы исходили из фиксированного количества ресурсов, выделенного для ее выполнения. Правда, в момент составления сетевого графика еще не бывают известны точные календарные сроки выполнения работ. Это выясняется лишь позже, после расчета основных временных показателей сетевого графика. Выделяя для каждой работы определенное количество ресурсов, мы могли предполагать их достаточность, исходя из наших возможностей. Однако не всегда учитываются совпадения сроков выполнения работ, при проведении которых используются одни и те же ресурсы. В результате может оказаться, что на ту или иную календарную дату потребуется ресурсов больше, нежели мы располагаем. Вот это и требуется проверить, прежде чем приступать к выполнению планируемого комплекса работ. Поэтому необходимо быть уверенным, что ограниченные, как правило, ресурсы позволят выполнить намечаемые работы.
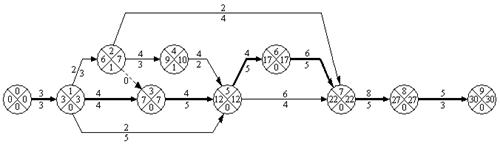
Продолжительность всего комплекса работ равна продолжительности критического пути. Анализ сетевого графика позволяет выделить те работы от которого она действительно зависит. Их число как правило, не велико по сравнению с общим количеством работ.
При обычных методах планирования комплекса работ для сокращения общего срока разработки не редко стремятся уменьшить продолжительность всех или большинства работ. Такой подход как правило, надает соответствующего эффекта, так как требует дополнительных затрат и незначительно сокращает продолжительность выполнения всего комплекса работ.
Важнейшим способом сокращения критического пути является использование определенной части ресурсов, для ускорения критических работ.
1.1.2. Математическая модель задачи
Для того чтобы выполнить оптимизацию сетевого графика, необходимо рассчитать и определить:
1. Необходимое число ресурсов для каждой работы:
A = B / Cгде A - необходимое число ресурсов;
B - объем работ;
C – производительность.
2. Продолжительности работ:
D = A / Fгде D – продолжительность работы;
A – необходимое число ресурсов;
F – число ресурсов.
3. Ранние сроки наступления событий:
tр (j) = max {tр (i) + t (ij)}, i<j, tр (0) = 0
где i, j – номера событий;
tр (i, j) – ранний срок наступления (i, j) события;
t (ij) – срок выполнения работы (i-j);
i<j – событие i предшествует j.
4. Поздние сроки наступления событий:
tп (i) = min {tп (j) - t (i,j)}, i<j
где i, j – номера событий;
tп (i, j) – поздний срок наступления (i, j) события;
t (ij) – срок выполнения работы (ij);
5. Полный резерв времени для каждой работы:
Rп(i,j)= tп(j) - tр(i) - t (i,j)
где i, j – номера событий;
tп (j) – поздний срок наступления события j;
tр (i) – ранний срок наступления события i;
t (ij) – срок выполнения работы (i-j).
6. События, лежащие на критическом пути. Такие события имеют равные ранние и поздние сроки наступления.
7. Критические работы. То есть работы, у которых начальное и конечное события критические.
8. Критический путь. Рассчитывается как сумма продолжительностей критических работ.
Далее проводится непосредственно оптимизация сетевого графика, т.е. в целях сокращения продолжительности критического пути программа предлагает пользователю перераспределить ресурсы с работ, находящихся на некритических путях, на выполнение работ, не имеющих резервов времени
Похожие работы
... в данной курсовой работе. В данном курсовом проекте рассматриваются цель: определить минимальную стоимость комплекса производственных работ при заданной продолжительности его выполнения и других указанных условиях. 1. ПОСТРОЕНИЕ СЕТЕВОГО ГРАФИКА Сетевой график - экономико-компьютерная модель, отражающая комплекс работ (операций) и событий, связанных с реализацией некоторого проекта ( ...
... на самом графике и табличный метод. В них полностью используются формулы аналитического метода. Методические указания по расчёту и оптимизации параметров сетевого графика приводятся по ходу решения задач. Расчёта и оптимизации сетевого графика Разработать план выполнения ОКР по созданию нового образца телевизора в виде сетевого графика на основе перечня работ и трудоёмкости их выполнения, ...
... работы, принадлежащие критическому пути, и тем самым уровнять длительности этих путей, для обеспечения выполнения критерия оптимальности (1.1). 2Теоретические основы сетевого планирования Прежде, чем преступать к обоснованию рациональных методик поиска особых путей сетевого графика, необходимо напомнить, что вообще собой представляет сетевой график, и какими основными параметрами он характеризу ...
... , тем ближе данный путь к критическому и наоборот и чем меньше коэффициент напряженности, тем большими резервами обладает данный путь [1]. Далее проводится анализ сетевого графика [2]. При этом определяется вероятность P наступления завершающего события в заданный срок. Для этого с помощью таблицы [3] определяется значение функции Лапласа Ф(Х): (6.12) ...




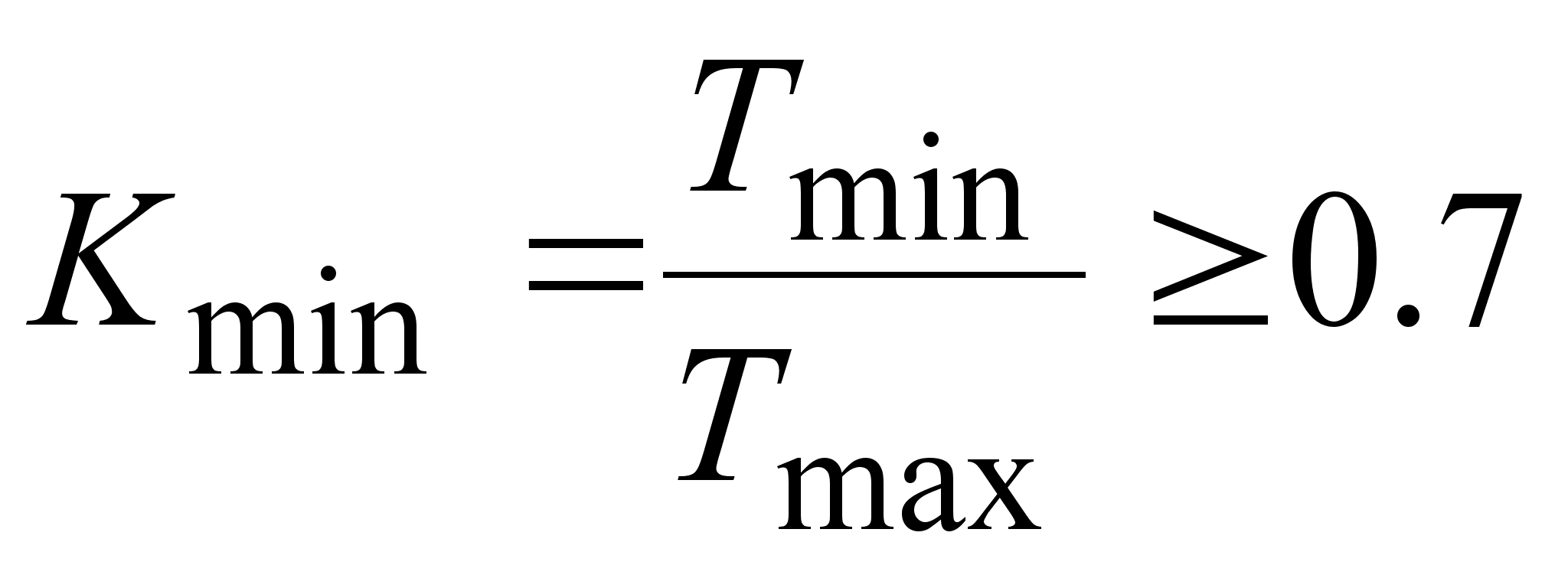

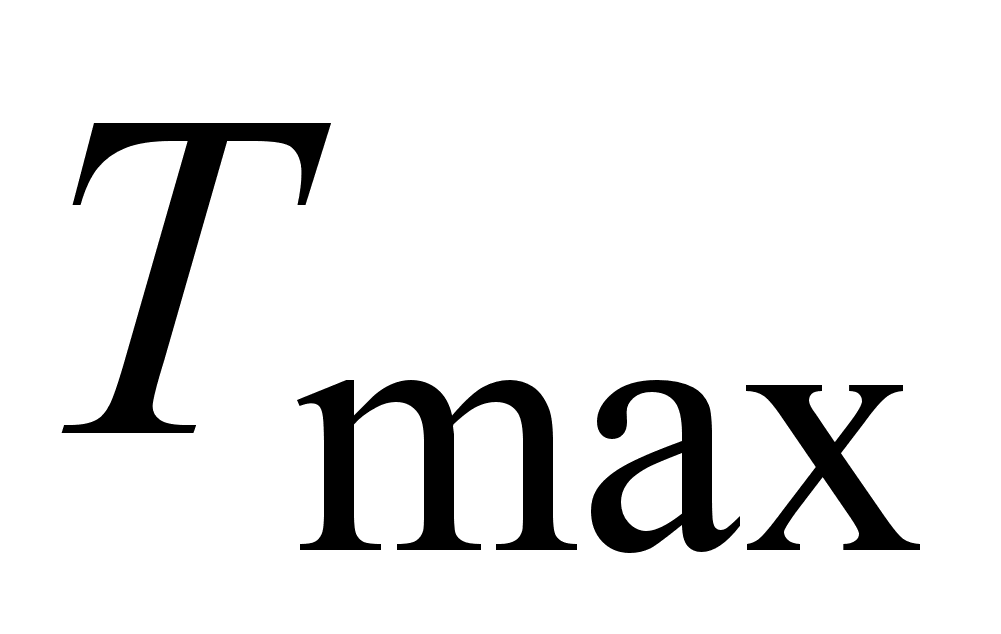
0 комментариев