Содержание
1. Анализ исходных данных и разработка ТЗ
1.1 Основание и назначение разработки
1.2 Постановка задачи в предметной области, разработка математической модели
1.3 Выбор и обоснование алгоритма решения задачи
1.4 Требования к функциональным характеристикам программы
2. Руководство пользователя
2.1 Назначение программы
2.1.1 Минимальные требования к составу и параметрам технических средств IBM совместимый персональный компьютер с CPU, начиная с 486 и выше
2.2 Минимальные требования к информационной и программной совместимости
2.3 Интерфейс пользователя
3 Руководство программиста
3.1 Функциональная схема
3.2 Тестовый пример
Используемая литература
1. Анализ исходных данных и разработка ТЗ 1.1 Основание и назначение разработки
Было получено задание, написать программу на языке программирования Visual Prolog, который был дан в качестве исходных данных. Программа на тему “Маршрутизация", а именно, поиск оптимального пути на маршрутном такси в Нижнем Новгороде. Назначение разработки - это изучение языка программирования Prolog. Эта программа должна быть полезной для навигации по нашему городу.
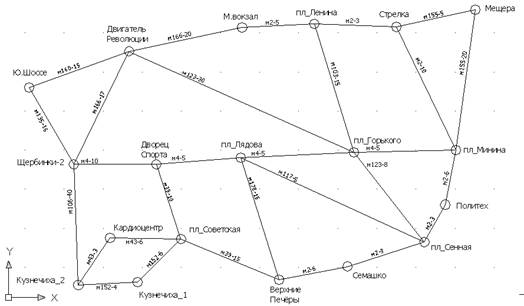
1.2 Постановка задачи в предметной области, разработка математической моделиСуть моей задачи заключается в отыскании оптимального пути от одной остановки до другой по Нижнему Новгороду на маршрутном такси. Исходя из того, что маршрутов в городе порядка пятидесяти, а остановки, я думаю что, исчисляются сотнями, то размерность задачи можно считать средней. При решении полным перебором, может возникнуть проблема, а именно, время отыскания пути может занять неопределённое время. Поэтому полный перебор здесь не подойдёт. Далее я выбрал геометрическую интерпретацию.
|
Набор понятий:
участок - определяет параметры ветки, в которые входит: начальная остановка, координаты её, следующая остановка, координаты её, номер маршрутного такси, на котором можно добраться от этих остановок, а также время прохождения.
участок (остановка1, х1, у1, остановка2, х2, у2, маршрутка, время).
принадлежит и принадлежит_симв - предикаты определяют принадлежность элемента списку, только в первом предикате список целочисленный, а во втором - строковый.
принадлежит (элемент, список).
min, max - возвращают соответственно минимальное и максимальное значения из двух.
min (первое, второе, минимальное).
max (первое, второе, максимальное).
коридор - принимает две остановки как входные данные и заполняет два списка, один по горизонтали (Х), а другой по вертикали (У). Эти два списка будут определять диапазон ветвей, которые будут участвовать в решении, а остальные просто-напросто отбрасываться, опираясь на то, что они все равно не дадут оптимального решения.
коридор (остановка1, остановка2, списокХ, списокУ).
добавить_в_диапазон - это предикат непосредственно заполняет список из целых цифр, лежащих в диапазоне от минимального до максимального значений с шагом равным единице.
добавить_в_дипазон (минимальное, максимальное, список).
мин_сумма1, мин_сумма2 - в совокупности определяют минимальный элемент в списке.
мин_сумма (минимальный, список).
путь - в общем-то, этот предикат самый основной. С помощью него происходит отыскание пути от остановки1 до остановки2 и суммы времени, которое необходимо затратить на преодоление данного пути.
список - список остановок. путь - список остановок и номеров маршрутных таски.
start -предикат, запускающий программу. Ему пользователь передаёт два значения (две остановки), а он возвращает путь и время. В ответе путь как переменная будет содержать не только остановки, но и маршрутные такси (их номера).
start (остановка1, остановка2).
В качестве математической модели я выбрал ненаправленный граф, у которого 19 вершин и 29 дуг. Где вершины графа - это остановки, а ветви - участки маршрутки, которые она может проехать не останавливаясь. Аббревиатура, например, м4-10 означает, номер маршрутного такси “4", время прохождения между вершинами десять минут. Как было сказано раньше полный перебор здесь не подходит, поэтому я определил понятие “коридор", который определяет диапазон дуг. (Суть “коридора" описывается ниже в алгоритмах). Граф, конечно, может и не только неориентированным, но и смешанным, т.е. маршрутка может проезжать по ветви только в одном направлении, а возвращаться по иной ветви. Мой граф имеет циклы, смежные вершины, а не только перекрёстки.
1.3 Выбор и обоснование алгоритма решения задачи
В моём случае граф представляется как сеть маршрутов маршрутных такси в Нижнем Новгороде. Вершины графа представляют собой остановки, а ветви их соединяют соответственно с определённой стоимостью. За стоимость я принял время прохождения маршрутного такси по ветви. Сеть, конечно же, предполагается очень густая. Моя цель на данном этапе - это определить наиболее оптимальный алгоритм поиска пути в нашем графе. Оптимальным он должен как с точки зрения процедуры поиска пути, так и сточки зрения результата, т.е. надо найти некую “золотую середину". Критерий оптимальности пути я выбрал время прохождения маршрутки, которое должно быть соответственно минимальным. Перейдём к поиску алгоритма.
1. Суть алгоритма, который мне пришёл на ум первым заключается в следующем: сначала поиск производится всех путей, а за тем в найденных путях по критерию наименьшей стоимости отбирается самый дешёвый. Стоимость складывается из цен каждой ветви. В таком алгоритме есть большой минус. Если граф будет состоять из большого числа ветвей, а в моём случае предполагается что город большой, значит и граф должен быть гутой, то поиск необходимого пути может занять неопределённое количество времени и в некоторых случаях персональный компьютер может просто зависнуть. Я считаю, что этот алгоритм оптимален сточки зрения результата. Потому что по этому алгоритму проверяются всевозможные пути. Но в таком случае он не оптимален с точки зрения процедуры поиска самого пути.
Значит, поиск оптимального пути должен производится не по всевозможным путям, а по путям, которые входят в некоторое подмножество. Отсюда следует следующий алгоритм.
2. По данному алгоритму вся карта делится на квадраты:
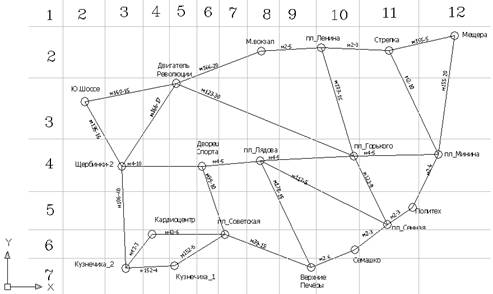
Каждый квадрат имеет пару координат. А в каждый квадрат могут попадать остановки, которые будут иметь координаты. В таком случае можно попробовать построить “коридор” от начальной остановки до конечной остановки. Этот “коридор” будет состоять из пары диапазонов: по вертикали и горизонтали. Диапазоны будут определяться из введённых пользователем данных: начальной и конечной остановок, которые в свою очередь имеют координаты. Теперь в полученном “коридоре" будет производиться поиск оптимального пути по предыдущему алгоритму. Недостаток этого алгоритма заключается в следующем: “коридор", который мы сформировали, может не иметь ветвей, и в таком случае решения мы не получим. Поэтому не стоит делать коридор узким. Наверное, стоит его сделать искусственно шире, т.е. расширить диапазоны. Конечно вероятность получить ответ увеличивается, но остается вероятность также не получить оптимального результата или не получить ответа вообще. Достоинство этого алгоритма перед предыдущим заключается в том, что поиск производится по ограниченному “коридором” - числу ветвей. Он оптимален с точки зрения процедуры поиска пути. В отличие от первого алгоритма мы можем, получит здесь путь по стоимости дороже, так как перебор ветвей ограничен.
3. Еще один алгоритм. Сохраним систему координат и понятие из предыдущего алгоритма. Будем двигаться от начальной остановки к конечной остановке, выбирая ветвь наименьшей цены. Этот алгоритм ещё называется градиентным. В таком алгоритме есть недостаток: полученный путь может получиться далеко не оптимальным.
4. Модифицируя предыдущий алгоритм: поиск пути от конечной остановки к начальной остановке. То есть берётся конечная остановка и ищется ветвь, примыкающая к ней с наименьшей ценой.
5. Сохраняем стратегию второго алгоритма и добавляем ограничение на прохождение по ветви в обратном направлении. Тем самым мы отбрасываем не нужные нам решения.
Для решения поставленной задачи я выбрал пятый алгоритм. Я считаю, что этот алгоритм в своём функционале имеет “золотую середину". Так как процедура поиска пути получается не очень объёмная, потому что ограничено количество ветвей “коридором", и происходит выбор пути из некоторого подмножества, а не сразу по некоторой эвристике. Объём этого подмножества, конечно, зависит не от объёма базы данных, а от того, на сколько удалены начальная и конечная остановки.
1.4 Требования к функциональным характеристикам программыПрограмма должна выполнять следующие функции:
Ввод исходных данных
Решение задачи - нахождение оптимального пути
Вывод найденного решения
2. Руководство пользователя 2.1 Назначение программы
Программа предназначена для поиска оптимального пути в Нижнем Новгороде на маршрутном такси. Или поиск пути в графе, где вершины графа - это остановки, а ветви - участки пути маршрутного такси. С помощью этой программы можно отыскать путь за минимальное время проезда от одной остановки до заданной. Результатом программы является список остановок и номеров маршрутных такси, которые расположены между остановками, и сумма времени. Из списка будет видно, что делать пользователю, а именно, пересаживаться на другое маршрутное такси или ехать дальше.
2.1.1 Минимальные требования к составу и параметрам технических средств IBM совместимый персональный компьютер с CPU, начиная с 486 и выше10Kb свободного пространства на HDD (для исходника)
15Mb RAM
Монитор
Клавиатура
2.2 Минимальные требования к информационной и программной совместимостиWindows 9х/NT/2000/ME (Visual Prolog 5.2 требует ОС типа Windows)
Visual Prolog 5.2
Поддержка операционной системой национальных шрифтов (кириллица)
2.3 Интерфейс пользователя
Для получения решения пользователь должен ввести запрос в формате: start (остановка1, остановка2). Где остановка1 - начальная остановка, а остановка2 - конечная. Результат решения:
Путь: ["остановка1","мi","остановкаQ",...,"мj"," остановка 2"]
Сумма_времени=Kyes
Так же результата решения может и не быть: “no", если нет таких пути, остановок, введённых в запрос пользователем. Поэтому требование к входным данным такое: остановки, введённые в запрос должны быть базе фактов.
Если пользователь захотел добавить ветвь, то ему необходимо добавить в базу фактов ещё один или два, один из которых обеспечивает не направленность ветки в формате:
участок (остановка1, х1, у1, остановка2, х2, у2, номер_маршрутки, время).
(участок (остановка2, х2, у2, остановка1, х1, у1, номер_маршрутки, время)) Для закрытии какой-нибудь линии необходимо сделать обратное J.
Для добавления новой остановки между двумя соединенными остановками надо отредактировать один факта и добавить новый и плюс два факта, описывающие обратные участки для всё той же не направленности веток и графа в целом:
участок (остановка1, х1, у1, остановкаNew, хN, уN, номер_маршрутки, время1).
NEW-участок (остановкаNew, хN, уN, остановка2, х2, у2, номер_маршрутки, время2).
(участок (остановкаNew, хN, уN, остановка1ew, х1, у1, номер_маршрутки, время1).
NEW-участок (остановка2, х2, у2, остановкаNew, хN, уN, номер_маршрутки, время2))
Для добавления новой остановки, не врезающейся в ветвь надо добавить факты, описывающие соединения этой остановки с другими.
3. Руководство программиста
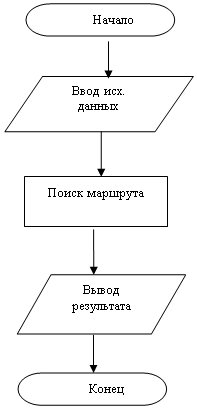 |
3.1 Функциональная схема
Логические модели. Блок-схемы алгоритма.
а) принадлежит (Х, [Х|_]).
принадлежит (Х, [_|Хвост]): - принадлежит (Х, Хвост).
см. Братко И. Программирование на языке Пролог для искусственного интеллекта.
б) max (X,Y,X): - X>Y.
max (X,Y,Y): - X<=Y.
min (X,Y,X): - X<Y.
min (X,Y,Y): - X>=Y.
см. Братко И. Программирование на языке Пролог для искусственного интеллекта.
в) мин_сумма1 (_, []).
мин_сумма1 (М, [Х|Список]): - М<=Х, мин_сумма1 (М, Список).
мин_сумма2 (М, [Х|Список]): - мин_сумма1 (М, Список),!;
мин_сумма2 (М, Список).
В данном случае конкретизирован Cписок, необходимо найти М. Присваиваем М значение первого элемента и сравниваем с остольными элементами списка. Если М является минимумом, то искомое значение найдено, отсечение не позволяет перейти ко второму условию этого правила. Иначе сравниваем с значения второго элемента списка с оставшимися. Цикл прекращается, если очередное значение М является минимальным.
г) коридор (Нач, Кон, СписокХ, СписокУ): -
участок (Нач, Х1, У1,_,_,_,_,_),!,
участок (_,_,_, Кон, Х2, У2,_,_),!,
min (Х1, Х2, МИН1),
max (Х1, Х2, МАКС1),
добавить_в_дипазон (МИН1, МАКС1, СписокХ),
min (У1, У2, МИН2),
max (У1, У2, МАКС2),
добавить_в_дипазон (МИН2, МАКС2, СписокУ).
Определяет координаты начальной и конечной остановки, минимальное и максимальное значения среди Х1, Х2 и У1, У2, затем уходит на правило, описанное в пункте д). Отсечение (зелёное) позволяет находить первое единсвенное решение, а остальные отбрасываютя, из-за идентичности.
д) добавить_в_дипазон (А, В, []): - А=В+1.
добавить_в_дипазон (А, В, [А|Список]): - А<=В, А1=А+1,добавить_в_дипазон (А1, В, Список).
А - минимальное значение, а В - максимальное. Список - дискретный набор целых чисел от А до В включительно с шагом в единицу. Пока А не равно В+1, А увеличивается на единицу и добавляется в голову Списка. Хвост в списке остаётся пустым.
е) путь (С, С,_, [С],_,_,0).
Путь с любой остановки в туже занимает время равное нолю, а список пути имеет только один элемент - начальная остановка. Так же этот предикат служит “заглушкой” для следующего правила, т.е. путь, найден, когда следующая остановка равна конечной. Конечная остановка добавляется в переменную Путь в виде списка. Время затраченное на прохождение ветви из конечной в начальную равняется нолю.
участок (Нач, След, Х2, У2, М, Время),
not (принадлежит_симв (След, Список)),
принадлежит (Х2, СписокХ),
принадлежит (У2, СписокУ), путь (След, Кон, [След|Список], Путь, СписокХ, СписокУ, Сумма1),
Сумма=Сумма1+Время.
Ветвь существует, если:
существует участок с первой начальной (последующей) остановкой и существующей следующей;
следующая остановка не принадлежит списку из предшествующих её остановок;
координаты следующей остановки принадлежат соответственным спискам, которые определяют “коридор".
Общая схема поиска пути (правило stsrt)
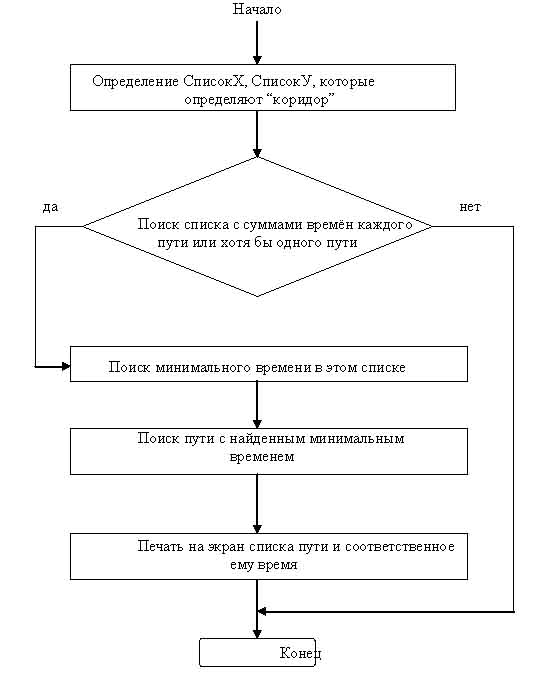
Блок-схема поиска отдельного пути (правило путь)
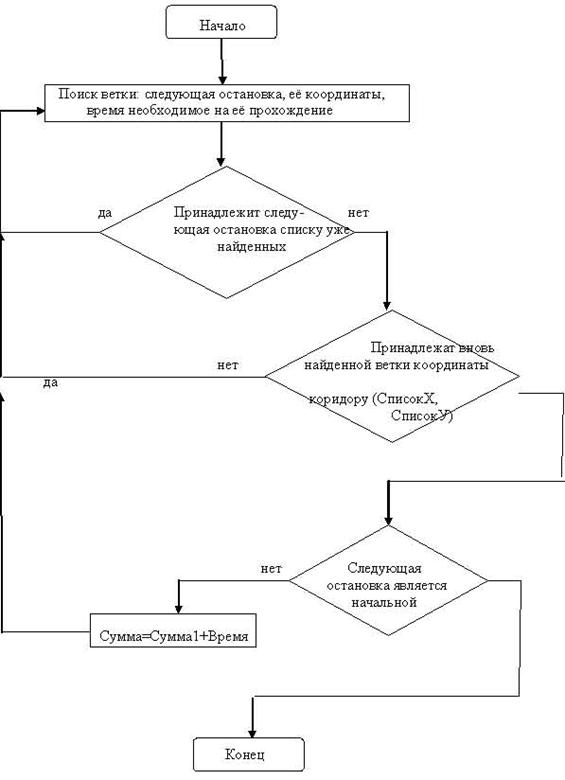
3.2 Тестовый пример
Выполним запросы:
а) start (кузнечиха_2, пл_сенная).
Решение:
Путь:
["кузнечиха_2","м43","кардиоцентр","м43","пл_советская","м39","в_печеры","м2","семашко","м2","пл_сенная"]
Сумма_времени=33yes
В решении используются факты, принадлежащие базе фактов, - факт24,26,21,31,34, также все факты и правила расположенные ниже базы фактов, кроме факта 60, который определяет путь, состоящий из одной остановки. Если, например, убрать факт21, то данного решения не будет, может, будет иное решение или решения вообще не будет. Проверив, я убедился, что решения нет. Убрав какое-нибудь из правил, вся программа “рухнет".
б) start (кузнечиха_2, кузнечиха_2).
Решение:
Путь: ["кузнечиха_2"]
Сумма_времени=0Yes
При решении затрагиваются: стартовое правило12 и факт 60, который и определяет это решение. Если его заремить, то решения не будет найдено.
в) Также ответ на запрос может быть “no" см. п.2.5
Используемая литература
1. Братко И. Программирование на языке Пролог для искусственного интеллекта: Пер. с англ. - М.: Мир, 1990. - 560 с., ил.
2. СТП 1-У-НГТУ-98 “Проекты (работы) дипломные и курсовые. Общие требования к оформлению пояснительных записок и чертежей"
Похожие работы
... 6) + 1 =(509 mod 6) + 1 = 5 + 1=6; Алгоритм на графах: поиск кратчайшего пути. 3) (Y mod 5) + 1 =(509 mod 5) +1 =4 + 1 = 5; Алгоритм сортировки: сортировка-шейкер. 2 АЛГОРИТМ СОРТИРОВКИ: СОРТИРОВКА ШЕЙКЕР 2.1 Математическое описание задачи Сортировка – это перестановка элементов некоторого множества в заданном порядке при некоторой упорядочивающей функцию. Сортировка используется для ...
... работы, принадлежащие критическому пути, и тем самым уровнять длительности этих путей, для обеспечения выполнения критерия оптимальности (1.1). 2Теоретические основы сетевого планирования Прежде, чем преступать к обоснованию рациональных методик поиска особых путей сетевого графика, необходимо напомнить, что вообще собой представляет сетевой график, и какими основными параметрами он характеризу ...
... не повторяются. Простой путь – путь, в котором дуги не повторяются. Маршрут – последовательность ребер, составляющих, как и путь, цепочку. Длина пути взвешенного графа определяется как сумма весов – его дуг. Если граф не взвешен, то можно считать веса дуг равными 1. Кратчайшим путем между выделенной парой вершин хн и хк называется путь, имеющий наименьшую длину среди всех возможных путей между ...
змы по-прежнему превосходили электронные, нам придётся поискать способ объединить компьютеры и человеческий мозг, либо попытаться искусственным путём усовершенствовать собственные гены. (Подробнее об этом рассказывается здесь) Впрочем, такие проекты пока остаются фантастикой. До их реализации пока ещё очень далеко, а пока главным предназначением устройств, подобных созданной в Мюнхене нейросхеме, ...
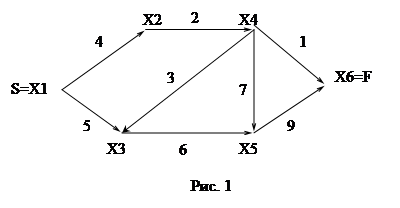
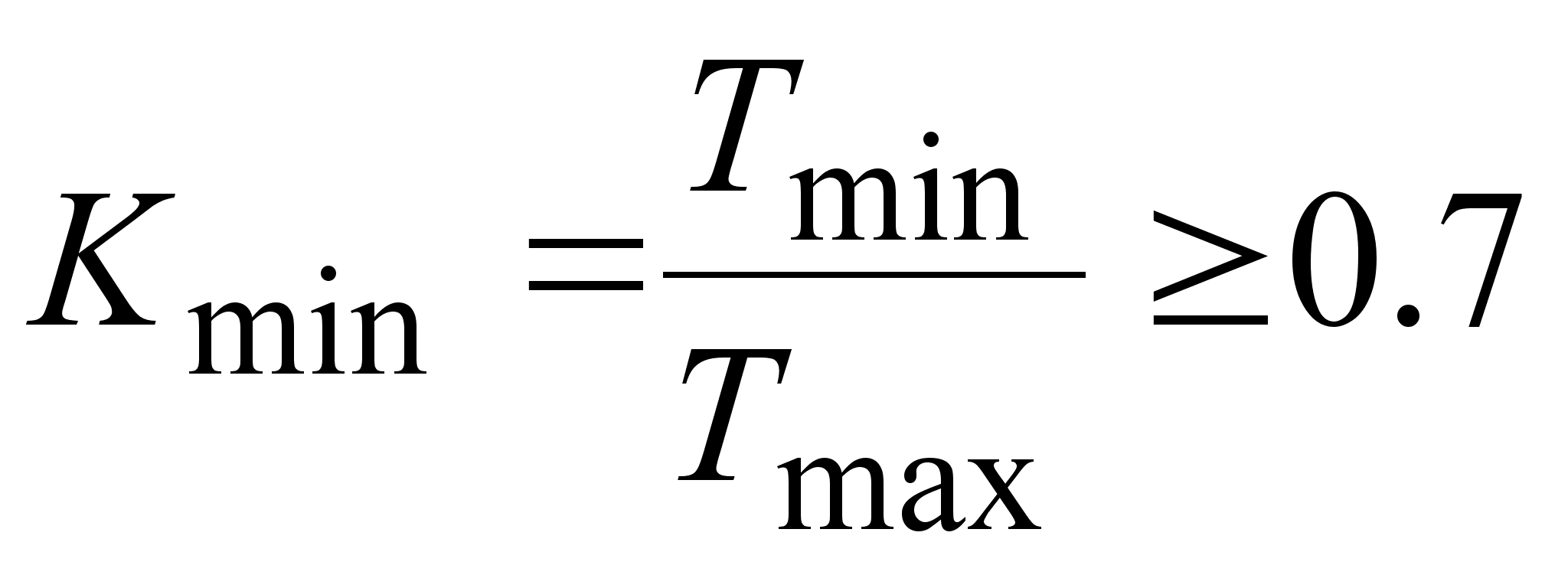

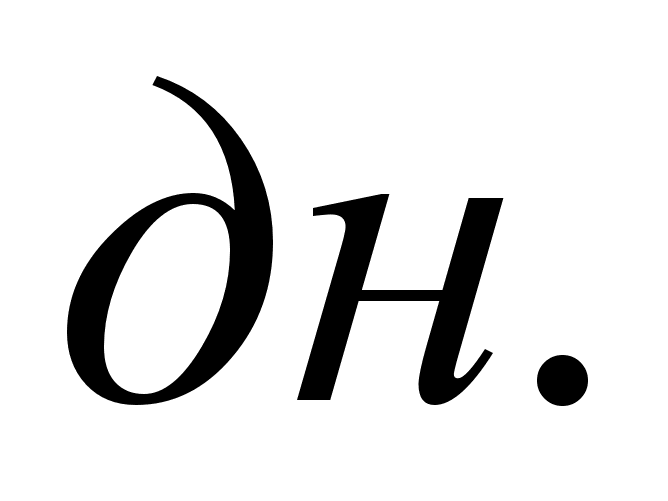
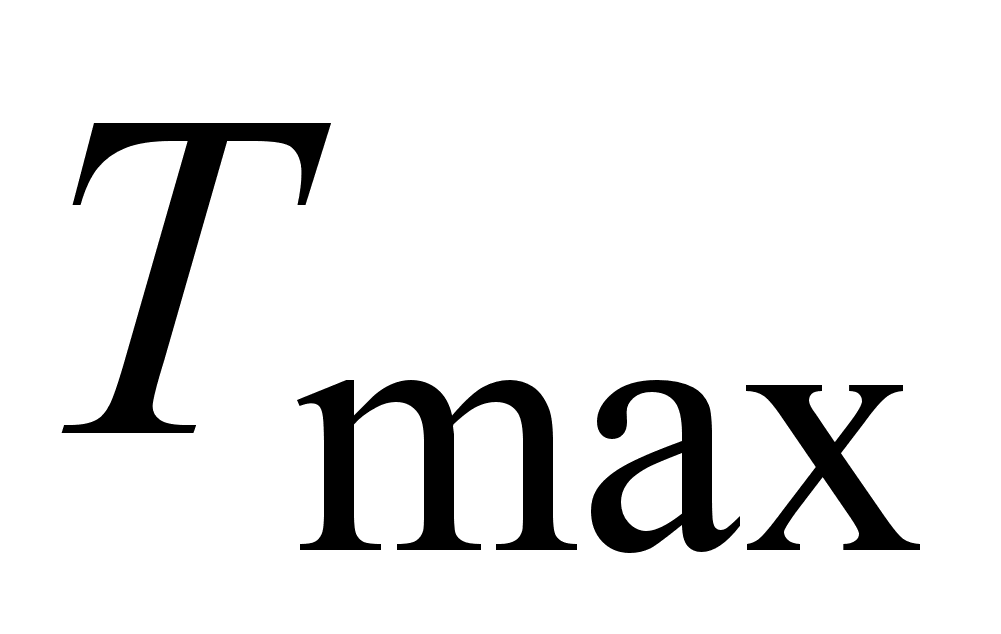
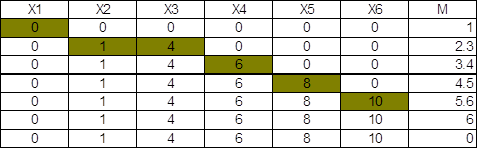


0 комментариев