Навигация
Представление знаний при помощи логики предикатов
4. Представление знаний при помощи логики предикатов
Логика предикатов базируется на логике высказываний, причем высказывание – это предложение, принимающее только два значения:
истина или ложь.
Например, у нас есть высказывания: «цена высокая», «цена низкая», «в отделе работает 15 человек». Из них можно получить:
Цена высокая или низкая.
Цена высокая и в отделе работает 15 человек.
Если Цена не высокая, то Цена низкая.
И наоборот, любое высказывание может быть разделено на несколько высказываний при помощи выделенных слов-связок.
Элементарные высказывания можно рассматривать как переменные, принимающие значения истина или ложь.
Обозначим элементарные высказывания символами А и В, а для обозначения выделенных слов-связок применим следующие символы:
ù – «не», Ú – «или», Ù – «и», É – «если».
Например, есть высказывание «Сидоров – бухгалтер».
Разобьем данное предложение на части – Сидоров (субъект), бухгалтер (свойства субъекта):
бухгалтер (Сидоров).
Или «Василий – начальник Петра»: тут два субъекта, и отношение между ними «.... – начальник .....», получаем:
начальник (Василий, Петр).
Вместо имен можно подставить переменные х, у, z, тогда:
бухгалтер (х),
начальник (у, z).
Рассмотрим предложение: У каждого бухгалтера есть начальник. Для формального представления этого предложения необходимо использовать конструкции вида:
«существует такой х, что ...», «для любого х ....».
Введенные допущения называются кванторами общности и существования:
"х( ),$у( ).
Тогда предложение можно записать: "х$у(бухгалтер(х) É начальник(х,у)).
Важна последовательность постановки кванторов: если переменим местами: $у"х (бухгалтер(х) É начальник(х,у)),
то это будет обозначать:
У всех бухгалтеров общий начальник.
Все принятые выше допущения образуют математический аппарат, алгебру предикатов.
Введем понятие предиката.
Функцию ![]() от буквенных переменных
от буквенных переменных ![]() , принимающую логические значения y (0 или 1), назовем n-местным предикатом или просто предикатом. Любой конечный предикат можно задать с помощью таблицы его значений, где каждому набору значений аргументов
, принимающую логические значения y (0 или 1), назовем n-местным предикатом или просто предикатом. Любой конечный предикат можно задать с помощью таблицы его значений, где каждому набору значений аргументов ![]() ставится в соответствие значение предиката у.
ставится в соответствие значение предиката у.
Алгебра предикатов характеризуется алфавитом букв А, состоящим из k различных символов ![]() и алфавитом переменных b, состоящим из n различных символов
и алфавитом переменных b, состоящим из n различных символов ![]() .
.
Для построения любой формулы будем пользоваться символами:
– буквами – ![]()
– переменными – ![]()
– знаками дизъюнкции – ‘Ú ’ и конъюнкции – ‘Ù’;
– скобками – ‘(’ и ‘)’;
– логическими константами – ‘0’ и ‘1’.
Под любой формулой алгебры конечных предикатов будем понимать:
а) формула может быть символом ‘0’ или ‘1’;
б) все выражения вида ai(xj), где индекс i изменяется от 1 до k, а индекс j – от 1 до n, также считаем формулами;
в) если выражения А и В являются формулами, то выражение ![]() (логическое сложение А и В) будет представлять из себя формулу.
(логическое сложение А и В) будет представлять из себя формулу.
г) если выражения А и В – формулы, то выражение ![]() (логическое умножение А и В) – называем формулой.
(логическое умножение А и В) – называем формулой.
Рассмотрим тождества алгебры предикатов:
Законы идемпотентности:
![]() ,
, ![]() .
.
Законы коммутативности:
![]() ,
, ![]()
Законы ассоциативности:
![]() ,
,
![]()
Законы элиминации (или поглощения):
![]() ,
,
![]()
Законы дистрибутивности:
A (BÚC) º AB Ú AC,
A Ú BC º (AÚB) (AÚC).
Тождества для констант:
![]() ,
, ![]() .
.
![]() ,
, ![]() .
.
Тождества для констант с отрицанием:
![]()
![]()
Закон двойного отрицания:
![]()
Закон исключенного третьего:
![]()
Закон противоречия:
![]()
Когда мы рассматривали пример:
Если цена не высокая, то цена низкая, то мы обратили внимание на связку: Если ...., то...., которую обозначили значком É.
Эта операция называется импликацией, и определяется как:
А É В º ù А Ú В,
где А и В – произвольные формулы алгебры предикатов,
º – операция, обозначающая тождественное равенство правой и левой части.
Читается так: «А влечет В», где А – посылка, В – заключение.
Рассмотрим свойства импликации:
1. Рефлективность импликации: ![]() .
.
2. Транзитивность импликации: ![]() .
.
Докажем данное тождество:
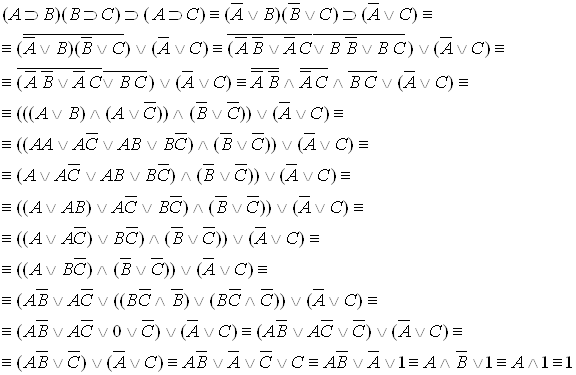
3. Свойства логических констант для импликации
![]() ,
, ![]() .
.
![]()
![]() .
.
4.Закон дедукции:
![]() .
.
5. Закон контрапозиции:
![]()
6. Закон импортации:
![]() .
.
7. Закон экспортации:
![]() .
.
8. Закон приведения к абсурду:
![]() .
.
9. Законы дистрибутивности:
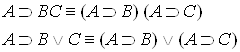 .
.
Похожие работы
... представлением двух основных парадигм научного знания: когнитивной лингвистики и функционально-прагматической лингвистики. Эти парадигмы функционируют путем конфигурации в исследовательской ситуации различных знаний. Во второй главе «Дискурс в предметной области “Горные экосистемы”» приведены основные характеристики научного дискурса, терминов и терминосистем; построена когнитивная модель ...
... разработка теоретического и практического материала для обеспечения доступного изучения соответствующих разделов по дисциплине Инженерия Знаний, а именно: представления знаний об объектах, представлении и использовании знаний об отношении между объектами, а также организации обобщенной информации на основе использования мультииерархической таксономической структуры. Практические разработки данного ...
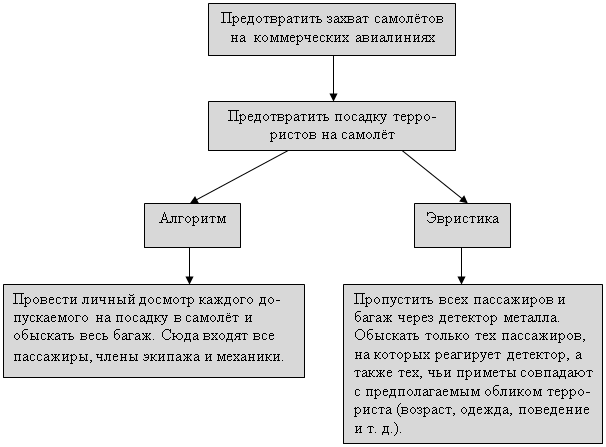
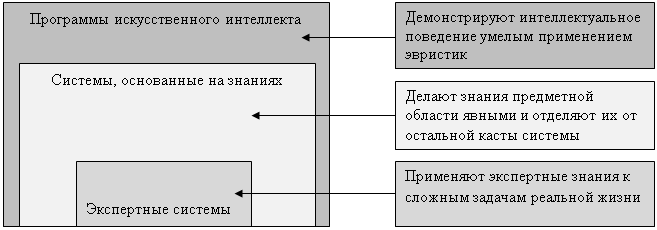
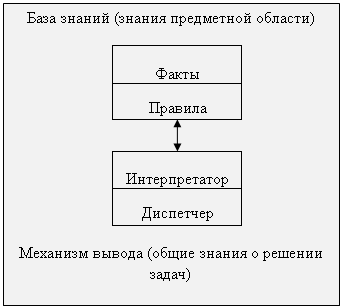
... в экспертной системе с необходимостью должны быть сложными либо в смысле сложности каждого правила, либо в смысле их обилия. Экспертные системы, как правило, работают с предметными областями реального мира, а не с тем, что специалисты в области искусственного интеллекта называют игрушечными предметными областями. В предметной области реального мира тот, кто решает задачу, применяет фактическую ...
... учитывать происходящие изменения. Поэтому ФС как модели представления знаний используются в тех предметных областях, которые хорошо локализуются и мало зависят от внешних факторов 2.3 Представление знаний в виде правил Такой способ является наиболее понятным и популярным методом формального представления знаний. Правила обеспечивают формальный способ представления рекомендаций, знаний или ...





0 комментариев