Навигация
Выражения для непрерывных функций Радемахера
10099
знаков
2
таблицы
17
изображений
1. Выражения для непрерывных функций Радемахера
![]()
![]()
![]()
![]()
![]()
![]()
2. Матрица для системы дискретных функций Радемахера при N = 5.
| Rad(0,t) | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Rad(1,t) | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 |
| Rad(2,t) | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 |
| Rad(3,t) | 1 | 1 | 1 | 1 | -1 | -1 | -1 | -1 | 1 | 1 | 1 | 1 | -1 | -1 | -1 | -1 | 1 | 1 | 1 | 1 | -1 | -1 | -1 | -1 | 1 | 1 | 1 | 1 | -1 | -1 | -1 | -1 |
| Rad(4,t) | 1 | 1 | -1 | -1 | 1 | 1 | -1 | -1 | 1 | 1 | -1 | -1 | 1 | 1 | -1 | -1 | 1 | 1 | -1 | -1 | 1 | 1 | -1 | -1 | 1 | 1 | -1 | -1 | 1 | 1 | -1 | -1 |
| Rad(5,t) | 1 | -1 | 1 | -1 | 1 | -1 | 1 | -1 | 1 | -1 | 1 | -1 | 1 | -1 | 1 | -1 | 1 | -1 | 1 | -1 | 1 | -1 | 1 | -1 | 1 | -1 | 1 | -1 | 1 | -1 | 1 | -1 |
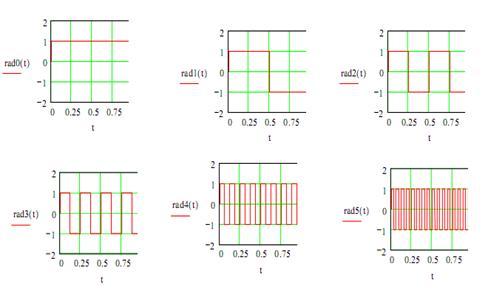
3. Графики функций от ![]() до
до ![]() .
.
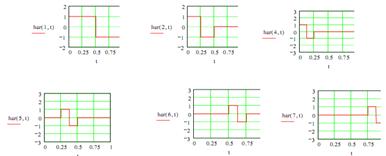
4. Выражение для нормированных функций Хаара.
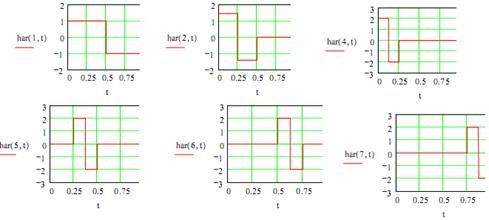
5. Графики нормированных функций от ![]() до
до ![]() .
.
6. Графики ненормированных функций от ![]() до
до ![]() .
.
 Выполнение работы
Выполнение работы 1. Используя преобразование Хаара рассчитаем амплитудный и фазовый спектр заданного сигнала
А. Используем нормированные функции Хаара.

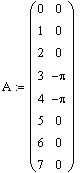
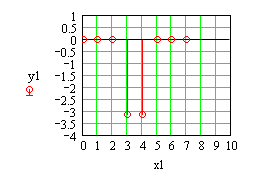
Б. Используем ненормированные функции Хаара
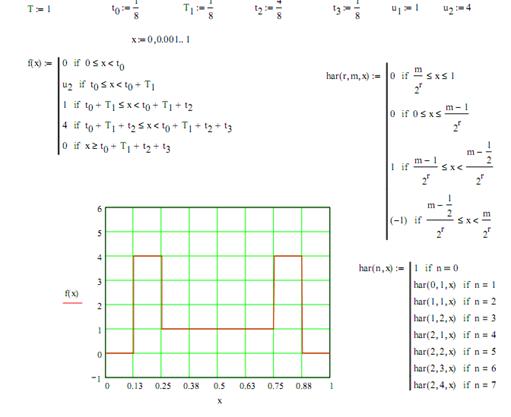
2. Синтезируем заданный сигнал и построим графики для обоих случаев
А. Используем нормированные функции Хаара
|
|
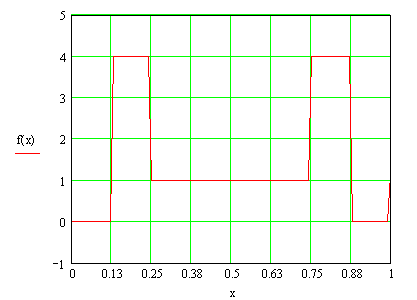
Б. Используем ненормированные функции Хаара


Выводы по работе
В данной лабораторной работе мы изучили особенности кусочно-линейных ортогональных функций Радемахера и Харра. Получили выражения для непрерывных функций Харра и Радемахера, построили графики этих функций. Построили матрицу для системы дискретных функций Радемахера при N = 5. Для функций Харра задали и построили графики нормированных и ненормированных функций. Получили практические навыки расчета спектров сложных сигналов, используя преобразование Хаара, найдя амплитудный и фазовый спектры заданного сигнала. После синтезирования сигналов, в случае нормированных функций Харра, получили исходный сигнал только после перехода на нормированное время. Это объясняется погрешностью программных расчетов. В случае же нормированных функций, заданный сигнал получить не удалось из-за, опять же, программных погрешностей вычисления.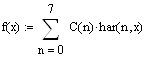
0 комментариев