Задача №1
Написать программу для вычисления значения выражения:
2
![]() 1+
1+
3+ 4
![]()
![]() 6
6
5+
7+x
при различных значениях х.
Предусмотреть программную обработку значений х, при которых выражение не существует.
Решение
1. Анализ введенных с клавиатуры исходных данных
2. Условие, при котором х > 0
3. Повторение предыдущей операции для каждой функции
4. Выведение условия для выхода
5. Вывод результатов
program Project1;
{$APPTYPE CONSOLE}
uses
SysUtils;
var
x,y,n:real;
begin
repeat
writeln('enter x');
readln(x);
if (x+7)=0 then writeln('resheniy net') else
if (5+6/(7+x))=0 then writeln('resheniy net') else
if (3+4/(5+6/(7+x)))=0 then writeln('resheniy net')
else
y:=1+2/(3+4/(5+6/(7+x)));
writeln('y=',y:1:10);
writeln('dly vuhoda nagmite 0, esli net to 1');
readln(n);
if n=0 then break
until false
end.
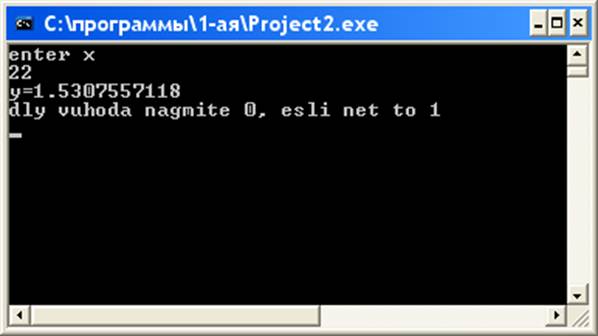
Рис. 1. Результаты работы программы для задачи 1
Задача №2
Шахматная доска содержит 8х8 клеток. Горизонтали и вертикали обозначаются цифрами 1-8. Написать программу, проверяющую, можно ли с первой заданной клетки попасть на вторую одним ходом черного слона.
Решение
1. Анализ введенных с клавиатуры исходных данных для первой клетки
2. Условие для а1 > 8 или в1 > 8.
3. Анализ введенных с клавиатуры исходных данных для второй клетки
4. Условие для abs (а2-а1).
5. Выведение условия для выхода
6. Вывод результатов
Для решения задачи введем координаты первой клетки, притом, что они должны быть меньше восьми; затем координаты второй клетки (они также должны быть меньше восьми). Если разность координат первой клетки равна разности координат второй клетки, то значит с первой клетки можно попасть на вторую одним ходом черного слона, если координаты не равны , то нельзя. Запишем результат.
program Project2;
{$APPTYPE CONSOLE}
uses
SysUtils;
var
a1,a2,b1,b2:integer;
c:real;
begin
repeat
writeln('Enter koordinati 1-oy kletki ot 1 do 8');
readln(a1,b1);
if (a1>8) or (b1>8) then writeln('Nelsya enter eto chislo, enter other');
writeln('Enter koordinati 2-oy kletki ot 1 do 8');
readln(a2,b2);
if abs(a2-a1)=abs(b2-b1) then writeln('mogno') else writeln('nelsya');
readln;
writeln('dly vuhoda nagmite 0, esli prodolgit to 1');
readln(c);
if c=0 then break;
until false
end.
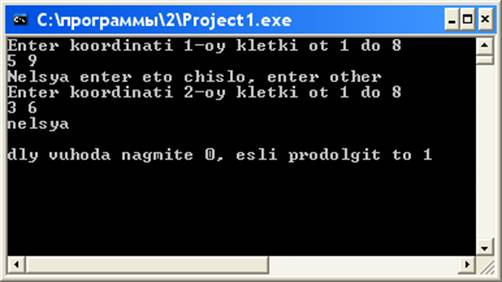
Рис.2. Результаты рабаты программы для задачи 2
Задача №3
Татьяна Ларина, читая очередной французский роман, подсчитала сумму номеров прочитанных страниц. Написать программу, определяющую номер последней прочитанной страницы.
Решение
1. Анализ введенных с клавиатуры исходных данных
2. Решение с помощью арифметической прогрессии
3. Выведение условия для выхода
4. Вывод результатов
program Project2;
{$APPTYPE CONSOLE}
uses
SysUtils;
var
sum,i,n:integer;
begin
write('enter n:');
readln(n);
i:=0;
repeat
inc(i);
sum:=sum+i;
until sum>=n;
writeln('otvet',i);
readln(i);
end.
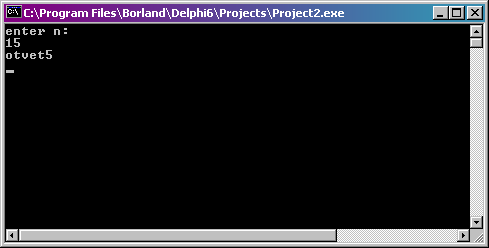
Рис. 3. Результаты работы программы для задачи 3
Задача №4
Найти все двузначные числа, сумма цифр которых не меняется при умножении на 2,3,4,5,6,7,8,9.
Решение
Для написания этой программы воспользуемся функцией sumc (умножение I на любое однозначное число ). Для проверки кратности удобно использовать операцию mod, позволяющую определить остаток при делении целых чисел. Так как числа двузначные, то цикл будет от 10 до 99.
program Project4;
//uses SysUtils;
var
sum, i : integer;
function sumc(val : integer) : integer;
var
x: integer;
begin
x:= 0;
repeat
x := x + val mod 10;
val := val div 10;
until val = 0;
sumc := x;
end;
begin
for i := 10 to 99 do
begin
sum := sumc(i);
if sumc(i*2) = sum then writeln('2: ', i);
if sumc(i*3) = sum then writeln('3: ', i);
if sumc(i*4) = sum then writeln('4: ', i);
if sumc(i*5) = sum then writeln('5: ', i);
if sumc(i*6) = sum then writeln('6: ', i);
if sumc(i*7) = sum then writeln('7: ', i);
if sumc(i*8) = sum then writeln('8: ', i);
if sumc(i*9) = sum then writeln('9: ', i);
ReadLn;
end.
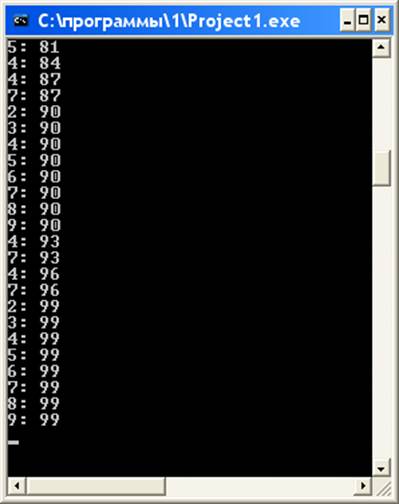
Рис. 4. Результаты работы программы для задачи 4
Задача №5
Одномерный массив, содержащий N элементов, состоит из нулей, единиц и двоек, расположенных в произвольном порядке (заполнение массива-случайным образом). Преобразовать массив так, чтобы вначале расположились все двойки, затем все нули и, наконец, все единицы.
Решение
program Project5;
//uses SysUtils;
const
n = 20;
var
arr : array [1..n] of byte;
tmp, i, j, k : byte;
begin
randomize;
for i := 1 to n do arr[i] := random(3);
for i := 1 to n do
for j := i to n do
if arr[i] < arr[j] then
begin
tmp := arr[i];
arr[i] := arr[j];
arr[j] := tmp;
end;
for i := 1 to n do if arr[i] = 1 then
begin
k :=i;
break;
end;
for i := k to n do
for j := i to n do
if arr[i] > arr[j] then
begin
tmp := arr[i];
arr[i] := arr[j];
arr[j] := tmp;
end;
for i := 1 to n do write(arr[i],' ');
ReadLn;
end.
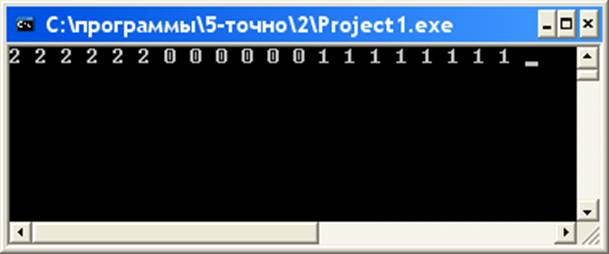
Рис. 5. Результаты работы программы для задачи 5
Задача №6
Задана матрица расстояний между городами. Написать программу, указывающую все города, расстояния от которых до других городов не больше А.
Решение
program Project6;
//uses SysUtils;
const
a = 20;
var
arr : array [1..5, 1..5] of byte;
i, j : byte;
begin
randomize;
for i := 1 to 5 do
for j := 1 to 5 do arr[i, j] := 0;
for i := 2 to 5 do
for j := 1 to i-1 do arr[i, j] := random(50)+1;
for i := 1 to 5 do
for j := 1 to 5 do if (arr[i, j] <= a) and (arr[i, j]<>0) then writeln(i, ' ', j, ' ', arr[i, j]);
ReadLn;
end.
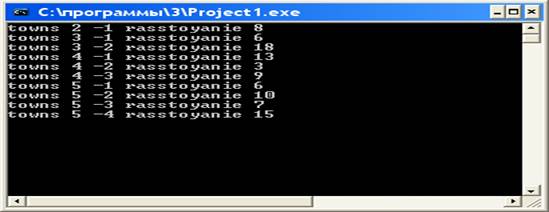
Рис. 6. Результаты работы программы для задачи 6
Задача №7
Удалить ведущие и конечные пробелы в строке.
Решение
1. Анализ введенных с клавиатуры исходных данных
2. Применение функции trim
3. Выведение условия для выхода
4. Вывод результатов
Для решения этой задачи используем строковый тип данных. Для удаления пробелов воспользуемся функцией trim(удаляет все ведущие и конечные пробелы). Запишем результат.
program Project7;
{$APPTYPE CONSOLE}
uses
SysUtils;
var
s:string;Index, Count:integer;
n:real;
begin
repeat
s:=('enter stroku s klaviaturi');
readln(s);
s:=trim(s);
writeln(s);
write('dly vuhoda nagmite 0, esli prodolgit to 1');
readln(n);
if n=0 then break
until false
end.
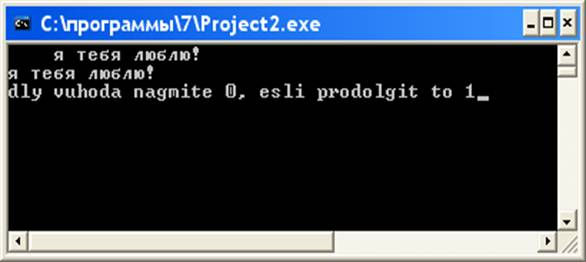
Рис.7. Результаты работы программы для задачи 7
Задача №8
Написать программу для удаления всех строк двумерного массива с отрицательными элементами.
Решение
Для решения задачи используем функцию haveotr, а также процедуру delete(удаляет из строки символы, начиная с позиции Index). Отметим, что haveotr=ложь, но если массив от 1 до 5 < 0, то в этом случае haveotr=правда.
program Project8;
//uses SysUtils;
var
arr : array [1..5, 1..5] of integer;
i, j : byte;
function haveotr(n : byte) : boolean;
begin
haveotr := false;
for j := 1 to 5 do if arr[n, j] < 0 then haveotr := true;
end;
procedure del(n : byte);
begin
for j := 1 to 5 do arr[n, j] ;
end;
begin
repeat
randomize;
for i := 1 to 5 do
for j := 1 to 5 do arr[i, j] := random(5)-1;
for i := 1 to 5 do
if haveotr(i) then del(i);
until false
end.
Задача №9
Даны два непустых множества прописных и строчных букв. Написать программу, которая выводит перечисленные множества в алфавитном порядке.
Решение
Для решения задачи вводим два непустых множества (случайным образом вдвоём буквы).N – число постоянное и равно 20. Вычисляем с помощью to length. Записываем результат.
program Project9;
//uses SysUtils;
const
n = 20;
var
tmp : char;
pr , st : string;
i, j : byte;
a:real;
begin
repeat
writeln('enter st');
readln(st);
for i := 1 to length(st) do
for j := i to length(st) do
if st[i] > st[j] then
begin
tmp := st[i];
st[i] := st[j];
st[j] := tmp;
end;
writeln('enter pr');
readln(pr);
for i := 1 to length(pr) do
for j := i to length(pr) do
if pr[i] > pr[j] then
begin
tmp := pr[i];
pr[i] := pr[j];
pr[j] := tmp;
end;
writeln(st);
writeln(pr);
write('dly vuhoda nagmite 0, esli prodolgit to 1');
readln(a);
if a=0 then break
until false
end.
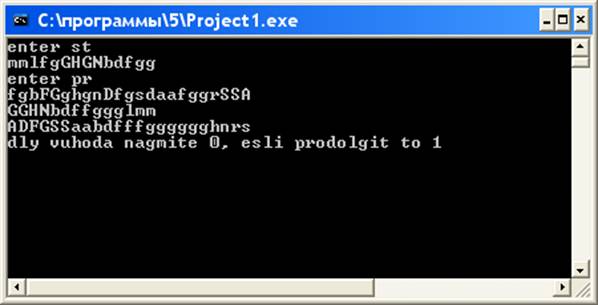
Рис. 9. Результаты работы программы для задачи 9
Задача №10
В файле целых чисел заменить все четные натуральные числа их квадратами.
Решение
program Project1;
//uses SysUtils;
var
n, i, tmp : integer;
Fin, Fout : text;
begin
assignfile(Fin, 'in.txt');
ReSet(Fin);
assignfile(Fout, 'out.txt');
ReWrite(Fout);
readln(fin, n);
for i := 1 to n do
begin
read(fin, tmp);
if tmp mod 2 = 0 then write(fout, tmp*tmp, ' ')
else write(fout, tmp, ' ');
end;
closeFile(Fin);
closeFile(Fout);
end.
Похожие работы
... области (если допустимая область ограничена и не пуста); 3. ограниченность целевой функции в допустимой области является необходимым и достаточным условием разрешимости задачи. Гл 2 Решение задач линейного программирования графическим способом на ЭВМ 2.1 Описание работы программы Программа написана с использованием собственных функций и процедур и трех стандартных модулей System, Crt и ...
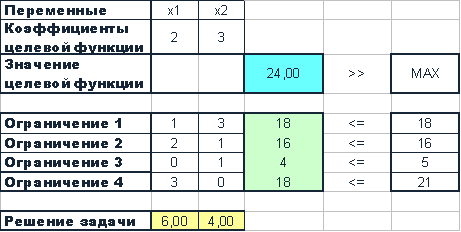
... от продажи одной единицы продукции и расход сырья на ее производство, надо составить оптимальный производственны план, дающий максимальную прибыль. В работе мы решим эту задачу классическим симплекс методом, средствами Excel и графическим методом. Глава 1. Решение задачи классическим симплекс методом Коэффициенты целевой функции Переменные целевой функции Задача при ограничениях ...
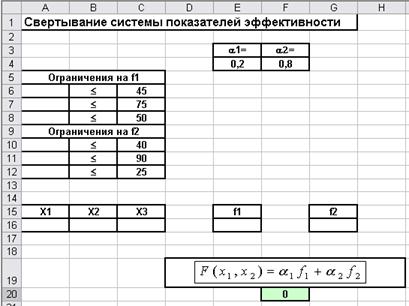
... эффективность: , где - прибыль (полезный эффект), - затраты. Этот метод часто называют методом “затраты – эффект”. Перейдем к рассмотрению информационных технологий решения ряда задач векторной оптимизации. В процессе рассмотрения мы ограничимся наиболее широко используемыми методами. Для решения задач будем использовать процессор электронных таблиц Excel, способный достаточно просто и ...
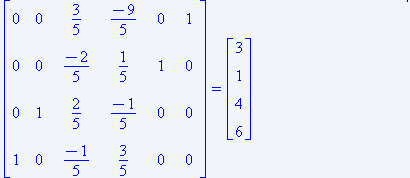
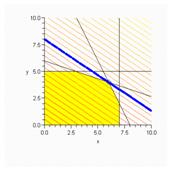
... . 1.3. Построение ограничений и градиента целевой функции : 1.4. Область допустимых решений – отрезок AB. 1.5. Точка А – оптимальная. Координаты т. А: ; ; . 2. Решение задачи линейного программирования симплекс-методом. Прямая задача. Задачу линейного программирования для любой вершины в компактной форме можно представить в виде: Для получения используем алгоритм, приведённый в ...




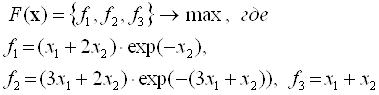
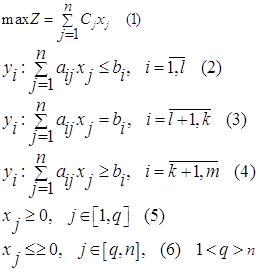
0 комментариев