Навигация
ОСОБЕННОСТИ РАБОТЫ В СРЕДЕ
3 ОСОБЕННОСТИ РАБОТЫ В СРЕДЕ
При написании программы использовалась среда Microsoft Visual C++ 6.0. Данная среда позволяет писать приложения на языке C++.
В ходе написания программы все операторы и служебные слова языка С++ выделяются другим цветом, чтобы отличать их от переменных, заданных программистом. Среда Microsoft Visual C++ 6.0 содержит встроенный компилятор.
Окно программы разделено на несколько частей. Вверху находится стандартная панель – Standart, с которой можно сохранить исходный текст программы на диск, открыть новый документ, скопировать или вставить текст, отменить последнее действие, или найти текст. Слева находятся панели Object TreeView и Object Inspector, на которых показаны объекты, которые используются в данной программе, и их свойства. В центре окна программы расположен текстовый редактор, в котором следует писать программу. Внизу – панель Output, в которой показывается сообщения, если в программе содержатся ошибки – компилятор сообщает вид ошибки и строку, в которой она допущена, достаточно сделать двойной клик левой клавишей мыши на описании ошибки в Output, чтобы переместиться на строку, содержащую ошибки.
Программа создана в консольном режиме – в режиме, не имеющем графического интерфейса.
4 ПРОГРАММНАЯ РЕАЛИЗАЦИЯ
4.1 Описание алгоритма и структуры программы
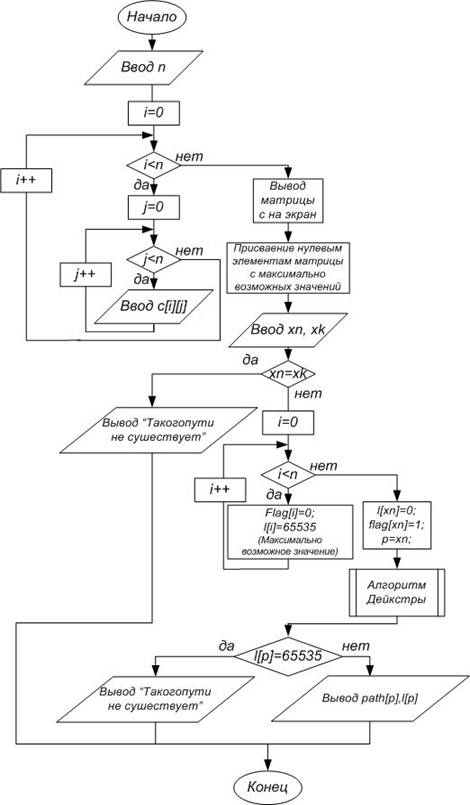
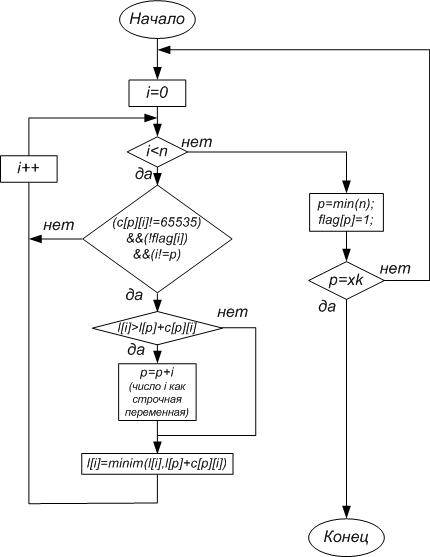
Рис. 4.1.1
Программа выводит минимальный путь между двумя указанными вершинами в графе и его длину.
При запуске программы на экран выводится запрос о вводе весов рёбер исследуемого графа. Данные, введённые пользователем, отображаются в виде матрицы смежности, в которой не существующие рёбра обозначаются нулями. После указанным рёбрам присваивается значение 65535, которое принимается за бесконечность.
Следующим этапом выполнения программы является запрос о вводе номеров вершин, между которыми необходимо узнать путь. В случае, если начальная и конечная вершины совпадают, отображается соответствующее сообщение и работа программы завершается. В противном случае выполняется непосредственно алгоритм Дейкстры, схема которого приведена в приложении В.
Результатом программы является вывод на экран вершин, через которые проходит минимальный путь, а также вывод длины маршрута. Если пути между заданными точками не существует – выводится соответствующее сообщение.
4.2 Описание использованных программных средств
Таблица 4.2.1–Описание переменных
| Переменная | Тип | Описание |
| n | int | Количество точек (вершин) грифа |
| i,j | int | Счётчики |
| p | int | Номер кратчайшего пути и наименьшей длины пути |
| xn | int | Номер начальной точки (вершины) |
| xk | int | Номер конечной точки (вершины) |
| flag[11] | int | Массив, i-й элемент которого имеет значение 0, когда i-й путь и расстояние временные, и принимает значение 1, когда i-й путь и расстояние становятся постоянными |
| c[11][11] | word (unsigned int) | Массив i-j элемент которого содержит расстояние между i-й и j-й точками (вершинами) Замечание: 1. с[i][i]=¥ 2. c[i][j]=c[j][i] |
| s[80] | char | Строчная переменная, которая содержит промежуточные значения пути |
| path[80][11] | char | Массив строк, который содержит пути Замечание: После прохождения обработки по алгоритму Дейкстры p-й элемент массива содержит кратчайший путь. |
| l[11] | word (unsigned int) | Массив, который содержит длины путей (path) Замечание: После прохождения обработки по алгоритму Дейкстры p-й элемент массива содержит длину кратчайшего пути. |
Кроме стандартных функций из библиотек iostream.h, string.h, stdio.h, conio.h были использованы также следующие функции.
· word minim(word x, word y) – функция, которая возвращает минимальное из x и y.
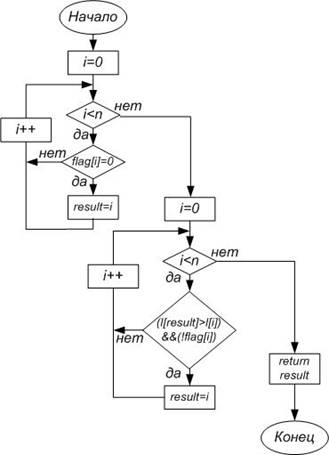
Рис. 4.2.1
· int min(int n) – функция, которая возвращает номер элемента массива l[i] минимальной «неотмеченной» длиной пути(flag[i]=0).
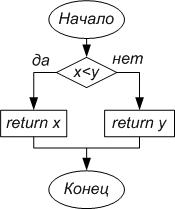
Рис. 4.2.2
5 ИНСТРУКЦИЯ ПОЛЬЗОВАТЕЛЯ
При запуске программы на экране появится окно с инструкциями. Выполняйте эти инструкции, а именно:
1. Введите количество вершин исследуемого графа.
2. Введите веса рёбер (положительное число). В программе расстояния от хi до xi+1 и xi+1 до хi считаются равными, а расстояния от хi до хi – не существующими. Если ребра между указанными вершинами не существует, введите 0 (ноль).
На экран выводится матрица смежности, отображающая введённую информацию.
3. Введите номер вершины, от которой начинается искомый путь.
4. Введите номер вершины, в которой путь заканчивается.
5. Чтоб завершить работу программы после получения результата нажмите Enter.
ЗАКЛЮЧЕНИЕ
Таким образом, в процессе создания данного проекта разработана программа, реализующая алгоритм Дейкстры в Microsoft Visual C++ 6.0. Её недостатком является примитивный пользовательский интерфейс. Это связано с тем, что программа работает в консольном режиме, не добавляющем к сложности языка сложность программного оконного интерфейса
Также были углублены знания, полученные в процессе выполнения лабораторных работ по предмету «Программирование».
ПЕРЕЧЕНЬ ССЫЛОК
1. Бондарев В.М. Программирование на С++.–Х: «Компания СМИТ», 2004
2. Страуструп Бьярн Язык программирования С++(2 ч).–«К:ДиаСофт», 1993
3. Хаханов В.И., Чумаченко С.В. Дискретная математика (теоретическое и практическое содержание курса).–Кафедра АПВТ, 2002
4. Алгоритм Дейкстры
5. Конспект лекций.
Приложение А
Текст программы
#include<iostream.h>
#include<string.h>
#include<stdio.h>
#include<stdlib.h>
#include<conio.h>
#define word unsigned int
int i, j, n, p, xn, xk;
int flag[11];
word c[11][11], l[11];
char s[80], path[80][11];
int min(int n)
{
int i, result;
for(i=0;i<n;i++)
if(!(flag[i])) result=i;
for(i=0;i<n;i++)
if((l[result]>l[i])&&(!flag[i])) result=i;
return result;
}
word minim(word x, word y)
{
if(x<y) return x;
return y;
}
void main()
{
cout<<"Vvedite kolichestvo tochek: ";
cin>>n;
for(i=0;i<n;i++)
for(j=0;j<n;j++) c[i][j]=0;
for(i=0;i<n;i++)
for(j=i+1;j<n;j++)
{
cout<<"Vvedite rasstoyanie ot x"<<i+1<<" do x"<<j+1<<": ";
cin>>c[i][j];
}
cout<<" ";
for(i=0;i<n;i++) cout<<" X"<<i+1;
cout<<endl<<endl;
for(i=0;i<n;i++)
{
printf("X%d",i+1);
for(j=0;j<n;j++)
{
printf("%6d",c[i][j]);
c[j][i]=c[i][j];
}
printf("\n\n");
}
for(i=0;i<n;i++)
for(j=0;j<n;j++)
if(c[i][j]==0) c[i][j]=65535; //бесконечность
cout<<"Vvedite nachalnuy tochku: ";
cin>>xn;
cout<<"Vvedite konechnuy tochku: ";
cin>>xk;
xk--;
xn--;
if(xn==xk)
{
cout<<"Nachalnaya I konechnaya tochki sovpadayt."<<endl;
getch();
return;
}
for(i=0;i<n;i++)
{
flag[i]=0;
l[i]=65535;
}
l[xn]=0;
flag[xn]=1;
p=xn;
itoa(xn+1,s,10);
for(i=1;i<=n;i++)
{
strcpy(path[i],"X");
strcat(path[i],s);
}
do
{
for(i=0;i<n;i++)
if((c[p][i]!=65535)&&(!flag[i])&&(i!=p))
{
if(l[i]>l[p]+c[p][i])
{
itoa(i+1,s,10);
strcpy(path[i+1],path[p+1]);
strcat(path[i+1],"-X");
strcat(path[i+1],s);
}
l[i]=minim(l[i],l[p]+c[p][i]);
}
p=min(n);
flag[p]=1;
}
while(p!=xk);
if(l[p]!=65535)
{
cout<<"Put: "<<path[p+1]<<endl;
cout<<"Dlina puti: "<<l[p]<<endl;
}
else
cout<<"takogo puti ne syshestvuet!"<<endl;
getch();
}
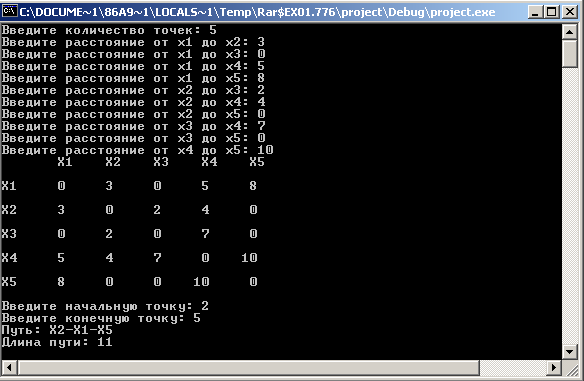
Приложение Б
Результат
Приложение В
Схема программной реализации алгоритма Дейкстры
Похожие работы
... подход к разработке эффективного алгоритма для решения любой задачи – изучить ее сущность. Довольно часто задачу можно сформулировать на языке теории множеств, относящейся к фундаментальным разделам математики. В этом случае алгоритм ее решения можно изложить в терминах основных операций над множествами. К таким задачам относятся и задачи информационного поиска, в которых решаются проблемы, ...
... образом. Пусть G=(V,E) in «D. Тогда множество вершин F(G) in «G совпадает с V, а множество дуг F(G) определяется применением следующих операций на E: a) удаляются все петли из Е; б) (v,w) заменяются на [v,w] для всех (v,w) in E. Тогда F(G) является графом, СВЯЗАННЫМ с орграфом G. Для орграфов понятие связности является более содержательным, чем для графов. Различают три важных типа связности ...
... же порты ввода-вывода или линии запроса прерывания. С такими проблемами, как конфликты различных частей аппаратуры, приходится иметь дело в основном именно операционным системам. Наконец, в-восьмых, при разработке операционных систем часто учитывается необходимость совместимости с предыдущей версией операционной системы. Система может иметь множество ограничений на длину слов, имена файлов и т. ...
0 комментариев