Навигация
Проект программного модуля для нахождения корня уравнения
Содержание
Введение. 2
1. Постановка задачи. 3
1.1 Математическая модель задачи. 3
1.2 Входные данные. 6
1.3 Выходные данные. 6
1.4 Обработка ошибок. 6
2 Проектирование программного модуля. 8
2.1 Структурная диаграмма программного модуля. 8
2.2 Разработка схемы программного модуля и её описание. 9
2.3 Разработка пользовательского интерфейса. 10
3 Реализация программного модуля. 12
3.1 Код программы.. 12
4 Тестирование программного модуля. 18
Заключение. 19
Список использованных источников. 21
Введение
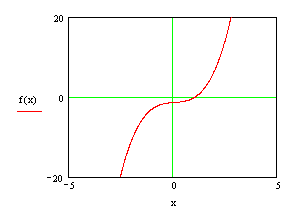
Целью данной курсовой работы является разработка программного модуля для нахождения методом хорд корня уравнения x3 - x - 0.3 = 0 с точностью до 0,001. Для разработки используется табличный процессор Excel и язык программирования Visual Basic for Application.
1. Постановка задачи
1.1 Математическая модель задачи
Рассматриваемый метод так же, как и метод деления отрезка пополам, предназначен для уточнения корня на интервале [a, b], на концах которого левая часть уравнения f(x) = 0 принимает разные знаки. Значение начала интервала а вводится с клавиатуры. Для определения значения конца интервала b, на котором функция меняет знак, при заданном значении начала отрезка а используют следующий итерационный алгоритм:
Задают начальное значение
х = a + h.
Здесь h – это заданный шаг изменения х.
Вычислить значения f(a) и f(x).
Если f(a) и f(x) имеют разные знаки, то принять b = x и прекратить вычисления, иначе принять
x = x + h
и перейти к шагу 2.
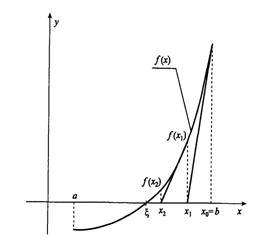
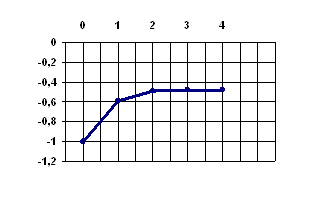
Очередное приближение теперь в отличие от метода деления отрезка пополам берем не в середине отрезка, а в точке х1, где пересекает ось абсцисс прямая линия, проведенная через точки f(a) и f(b) (рисунок 1).
В качестве нового интервала для продолжения итерационного процесса выбираем тот из двух [a, x1] или [x1, b], на концах которого функция f(x) принимает значения с разными знаками. Заканчиваем процесс уточнения корня, когда расстояние между очередными приближениями станет меньше заданной точности e
|xn – xn-1| < e
или когда значения функции f(x) попадут в область шума (рисунок 1), т. е.
|f(xn)| < e1.
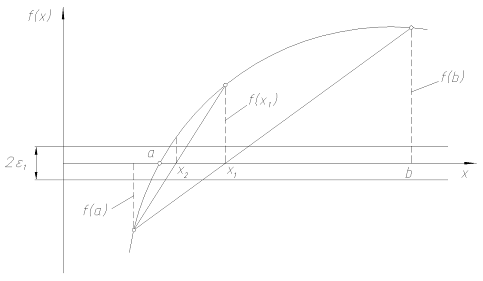
Рисунок 1. Метод хорд.
Уравнение прямой линии, проходящей через точки fa = f(a) и fb = f(b), запишем в общем виде
y(x) = kx + c .
Коэффициенты k и c уравнения этой прямой определим из условий
fa = ka + c ,
fb = kb + c .
Вычитая левые и правые части последних соотношений, получим
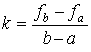 ,
,
c = fa – ka .
Точку пересечения прямой y(x) с осью абсцисс получим, приравнивая y(x) нулю
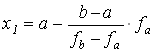 (1)
(1)
или
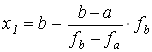 .(2)
.(2)
При заданной точности e метод состоит из таких шагов:
Вычислить f(a) и f(b) .
Вычислить x1 по формуле (1) или по формуле (2).
Если f(x1) = 0, то принять в качестве решения значение x1, вывести его и прекратить вычисления, иначе перейти к шагу 4.
Если f(x1) и f(a) имеют одинаковые знаки, то заменить a на x1.
Если f(x1) и f(b) имеют одинаковые знаки, то заменить b на x1.
Если |b - a| £ e (e - заданная погрешность вычислений) или |f(x1)| < e1 (e1 – заданное значение шума), то принять в качестве решения последнее значение x1, вывести его и прекратить вычисления, в противном случае перейти к шагу 2.
1.2 Входные данные
Входными данными являются:
Начало отрезка;
Конец отрезка;
Требования к входным данным:
Предусмотреть проверку на допустимость исходных данных и повторение ввода при ошибочных данных;
Ввод исходных данных осуществлять в поля ввода формы.
1.3 Выходные данные
Выходными данными являются:
Таблица вычислений;
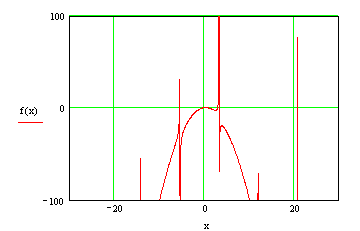
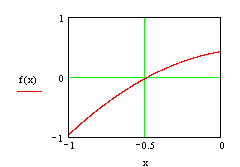
График функции.
Требования к выходным данным:
Все выходные данные выводятся на форму;
Ко всем выходным данным должен быть запрещен доступ со стороны пользователя.
1.4 Обработка ошибок
В данной программе реализован следующий способ контроля ввода:
Сначала проверяется, является ли набираемый символ либо цифрой, либо запятой;
Если не является, то набор символа игнорируется;
Если набираемый символ является цифрой, то он вводится в поле ввода;
Если набираемый символ является запятой, то проверяется, является ли
она первой вводимой запятой. Если ранее запятые не вводились, то она вводится в поле ввода. В противном случае ввод запятой игнорируется.
Данный способ контроля ввода реализован с помощью функции KeyPress.
Однако пользователь может не ввести в поле ввода данные. В этом случае выдается следующее сообщение:

Рисунок 2. Сообщение об ошибке.
Если пользователь ввел начало отрезка больше, чем конец отрезка, то в этом случае выдается следующее сообщение:
Рисунок 3. Сообщение об ошибке.
Похожие работы
... 3. Для функционирования программы необходима операционная система MS DOS 3.30 и выше или полностью совместимой с ней. Исходный текст программы написан на языке программирования высокого уровня Турбо Паскаль версии 7.0 фирмы Borland для DOS и WINDOWS с применением библиотеки Turbo Vision и содержится в файле notebook.pas в форме пригодной к использованию его как текстового документа в среде ДОС, и ...
... 35437 x4=0.58554 5 x1=1.3179137 x2=-1.59467 x3=0.35371 x4=0.58462 6 x1=1.3181515 x2=-1.59506 x3=0.35455 x4=0.58557 5. Сравнительный анализ различных методов численного дифференцирования и интегрирования 5.1 Методы численного дифференцирования 5.1.1 Описание метода Предположим, что в окрестности точки xiфункция F (x) дифференцируема достаточное число раз. ...
... файл kursach.ехе. Для функционирования программы необходим персональный компьютер с установленной операционной системой MS-DOS 3.30 и выше или полностью совместимой с ней. Исходный текст программы написан на языке программирования высокого уровня С++ фирмы Borland версии 3.1 для DOS и WINDOWS и содержится в файле kursach.срр в форме пригодной к использованию его как текстового документа в ...
... данных по сети. ЗАКЛЮЧЕНИЕ В рамках данного дипломного проектирования перед студентом Малышевым А.А. была поставлена задача: на основе алгоритма RSA для шифрования блоков данных, построить алгоритм и реализовать программный продукт для шифрования потоков данных. В результате выполнения дипломного проектирования был составлен принципиальный алгоритм для решения поставленной задачи. Далее он был ...
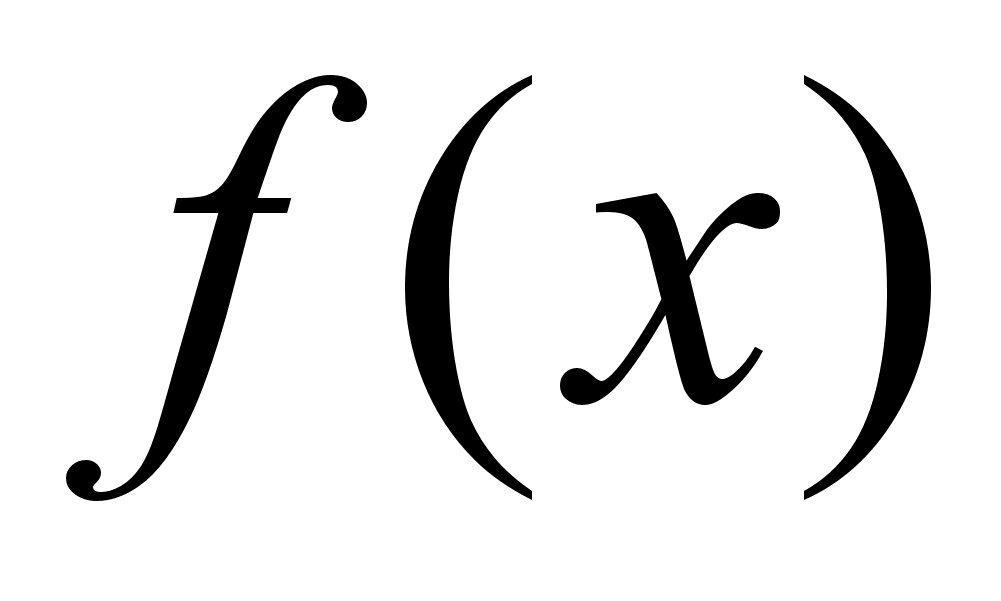
0 комментариев