Навигация
Використовуючи функцію Find;
1 Використовуючи функцію Find;
2. матричним способом і використовуючи функцію lsolve. Зрівняти результати.
Система лінійних рівнянь

Рішення засобами MS Excel
Для рішення рівнянь необхідно таблицю з вихідними даними та розрахувати по формулам.

Рисунок 2.1 – Система рівнянь в MS Excel
Правильність рішення системи рівняння можна простежити, якщо включити режим відображення формул.
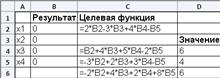
Рисунок 2.2 - Дані в режимі відображення формул

Рисунок 2.3 - Вікно пошуку рішень
При натисканні клавіші "Виконати" на екрані з'являється вікно «Результати пошуку рішення»
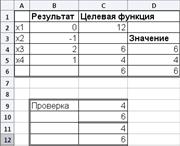
Рисунок 2.4 - Результат рішення та перевірка
Результат: х1=0, х2=-1; хЗ=2; х4=1
Рішення рівнянь за допомогою MathCAD
Рішення даної системи рівняння можна знайти за допомогою розв'язуваного блоку Given…Find.

Рисунок 2.5. Рішення рівнянь в MathCAD
Результат: x1=1, x2=1, x3=1, x4=1
2.2 Завдання 1.2Варіант 29
Перетворити модель, задану у виді системи нелінійних рівнянь до виду f 1(x) = y і f 2 (y)= x. Побудувати їхні графіки і визначити початкове наближення рішення. Вирішити систему нелінійних рівнянь.

Необхідно знайти інтервали значень функції для x та y таким образом:
Інтервал значень y:
-cos(x+2)+y=1.8
cos(x+2) = y-1.8
-1≤y-1.8≤1
0.8≤y≥2.8
Інтервал значень x:
cos(y-2)+x=0.3
cos(y-2)=0.3-x
-1≤0.3-x≤1
-1.3≤-x≤0.7
-0.7≤x≤1.3
Рішення засобами Excel.
Дану систему рівнянь можливо вирішити використовуючи команду «Пошук рішення».

Рисунок 2.6 - Дані в режимі відображення формул
Вікно «Пошук рішення» необхідно заповнити наступним чином:
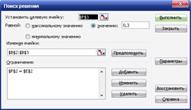
Рисунок 2.7 – Вікно пошуку рішень
Після виконання команди «Пошук рішення» ми побачимо результат обчислень:
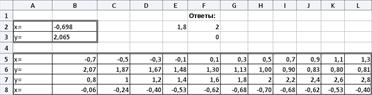
Рисунок 2.8 – Вікно з рішеннями
Виходячи із отриманих даних необхідно побудувати графік функції:
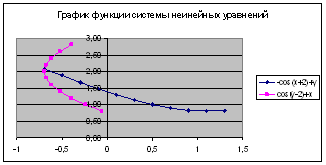
Рисунок 2.9 – Графік функції системи нелінійних рівнянь
Результат: x= -0.698, y= 2.065
Рішення засобами MathCAD
Рішення даної системи рівняння можна знайти за допомогою розв'язуваного блоку Given...Find.
З використанням функції Find знаходимо точне рішення системи рівнянь.
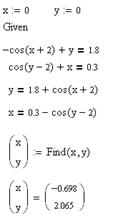
Рисунок 2.10 – Рішення системи нелінійних рівнянь

Рисунок 2.11 – Перевірка рішення системи нелінійних рівнянь
Результат: x= -0.698; y= 2.065
2.3 Завдання 2.1
Задача А. Вирішити задачу проектування конусоподібного фільтра.
З круглої заготівлі (r = 2) фільтрованого паперу вирізають сектор з кутом θ, потім з іншого роблять фільтр у виді конуса. Необхідно розрахувати величину кута θ, при якій забезпечується максимальний обсяг конуса (рис.2.12).
R – радіус основи конуса; h – висота конуса; r – радіус заготівлі фільтрованого папера.

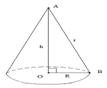
Рисунок 2.12 – Окружність та конус
![]() – довжина
– довжина
![]() – формула для куска дуги
– формула для куска дуги
Знаходимо різницю ![]()
![]()
У конусі получили прямокутний трикутник АОВ, кут О = 90о, h – катет у прямокутному трикутнику. Для знаходження катетів обчислимо корінь із різниці гіпотенузи r та катета R.
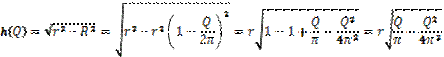
![]()
![]()
Цільова функція має вид:
![]()
Обмеження: ![]()
Розв’язання засобами Excel

Рисунок 2.13 – Розв’язання в Excel
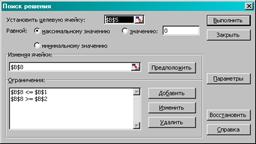
Рисунок 2.14 – Пошук рішення
Результат: кут θ дорівнює 66 градусів.
Рішення засобами MathCAD
Для рішення у MathCAD необхідно задатися початковими значеннями:
З використанням функції Maximize знаходимо оптимальний обсяг конуса.
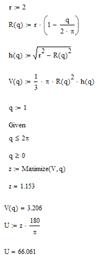
Рисунок 2.15 – Розв’язання в MathCAD
Результат: кут θ дорівнює 66 градусів.
Задача Б. Проектування 2 -х конусоподібних (пожежних) ребер.
З круглої заготівлі жерсті (r = 3) вирізають сектор з кутом ![]() , потім з іншого роблять цебро у виді конуса і з вирізаного сектора теж (тобто 2-а цебра) (рис.2.20).
, потім з іншого роблять цебро у виді конуса і з вирізаного сектора теж (тобто 2-а цебра) (рис.2.20).
Необхідно розрахувати величину кута ![]() , тобто як необхідно розкроїти заготівлю, щоб обсяг 2-х цебер був максимальним.
, тобто як необхідно розкроїти заготівлю, щоб обсяг 2-х цебер був максимальним.
R – радіус основи конуса; h – висота конуса; r – радіус заготівлі.
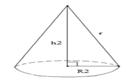
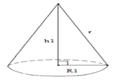
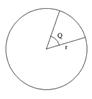
Рисунок 2.16 – Окружність, велика заготівля, маленька заготівля
Формули для знаходження радіусу R, висоти h та обсягу V великої заготівлі:
![]()
![]()
![]()
Формули для знаходження радіусу R, висоти h та обсягу V маленької заготівлі:
![]()
![]()
![]()
Цільова функція має вид:
![]()
Обмеження: ![]()
Розв’язання засобами Excel
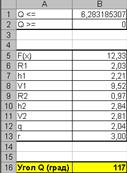
Рисунок 2.17 – Розв’язання в Excel
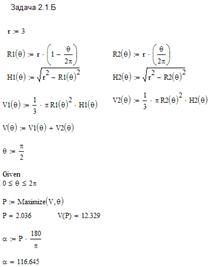
Рисунок 2.18– Розв’язання в MathCAD
Результат: кут θ дорівнює приблизно 117 градусів.
Задача 16. При яких розмірах прямокутного басейну даної місткості V(x,y,z) = 220м3 на облицювання його стін і дна буде потрібно найменша кількість матеріалу, тобто мінімум S(x,y).
Заносимо початкові в таблицю:
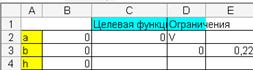
Рисунок 2.19– Таблиця початкових даних
Для перевірки правильності введення формул необхідно включити режим відображення формул:

Рисунок 2.20– Дані в режимі відображення формул
Вікно «Пошук рішення» необхідно заповнити наступним чином:
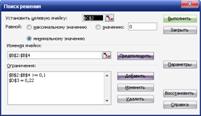
Рисунок 2.21– Вікно пошуку рішень
![]()
Рисунок 2.22– Вікно з рішеннями
Рішення рівняння за допомогою MathCad
Так як наша задача полягає у знаходження мінімальної кількості матеріалу для виготовлення ємності, ми скористуємося функцією Minimize.

Рисунок 2.23 – Рішення задачі засобами MathCAD
Результат: a=0,76; b=0.76; h=0.38; S=0.1733.
Похожие работы
... " констатує: "Держава проголошує туризм одним з пріоритетних напрямів розвитку національної культури та економіки і створює сприятливі умови для туристичної діяльності." Основними цілями державного регулювання в туризмі є: – забезпечення закріплених Конституцією України прав громадян на відпочинок, свободу пересування, відновлення і зміцнення здоров'я, на безпечне для життя і здоров'я довкілля, ...
... , виступають як методи менеджменту. У загальноприйнятому розумінні методи — це сукупність способів і засобів впливу суб'єкта управління на об'єкт з метою досягнення поставлених цілей. Методи менеджменту на підприємстві орієнтовані насамперед на високу продуктивність і ефективність діяльності персоналу, на злагоджену роботу підрозділів, на чітку організацію діяльності. Їх можна поділити на методи ...
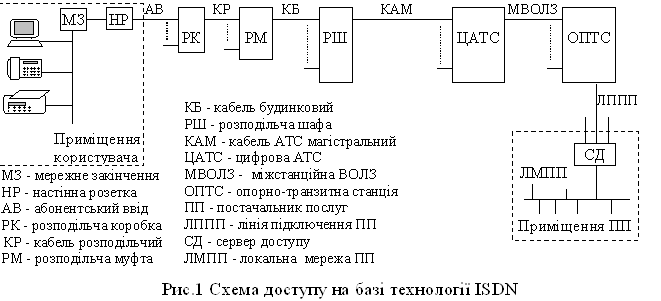
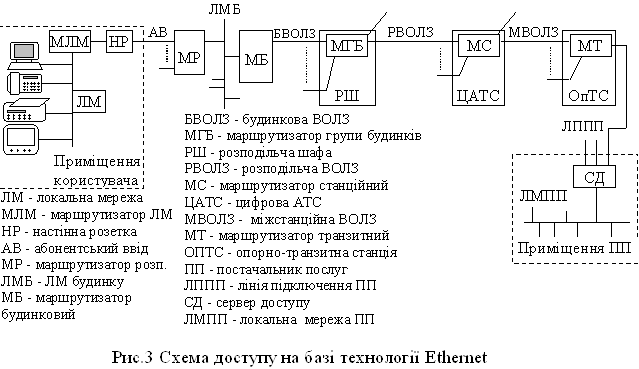
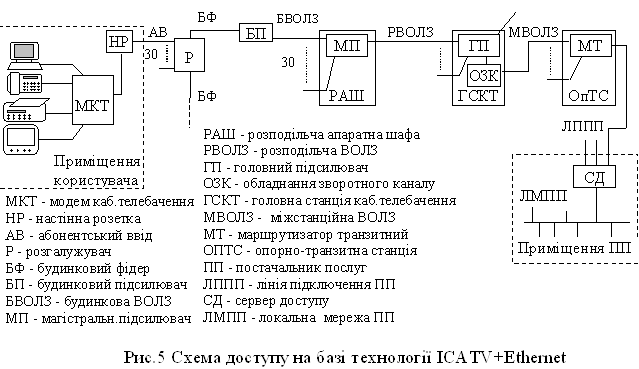
... - - - - - 1000/ТЗБ 20000 … 80000 3000 1500 2000 17000 100 50 200 30 Лабораторна робота № 3 РОЗРОБКА ТЕХНІЧНОГО ПРОЕКТУ МЕРЕЖІ ДОСТУПУ ЗАГАЛЬНОГО КОРИСТУВАННЯ 1. Мета роботи 1.1 Ознайомлення з етапом технічного проектування мереж зв’язку. 1.2 Оцінки пропускних здатностей ліній і трактів, а також їх вартості. 1.3 Вибір типів обладнання для вузлів ...
... 2. Розрахунково-аналітична частина 2.1 Визначення загального об’єму ремонтно-обслуговуючих робіт і обґрунтування програми центральної ремонтної майстерні У завданні на курсове проектування стоїть задача розробити проект організаційної структури та структури управління цеха на 5000 одиниць відновлення деталей типу «вал» у ВАТ «Житомирська райагропромтехніка». Деталі типу «вал» складають бі ...





0 комментариев