Навигация
Рассмотрим нерегулярный случай, когда матрица, полученная в результате подобных преобразований приведена уже к виду
2. Рассмотрим нерегулярный случай, когда матрица, полученная в результате подобных преобразований приведена уже к виду
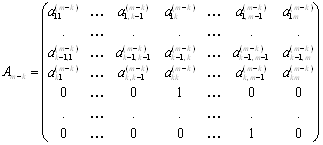 и элемент
и элемент ![]() .
.
Таким образом обычная процедура метода Данилевского не подходит из-за необходимости деления на ноль. В этой ситуации возможно два случая.
2.1 Предполагаем, что левее ![]() есть элемент
есть элемент ![]()
![]() Тогда домножая матрицу
Тогда домножая матрицу ![]() слева и справа на элементарную матрицу перестановок
слева и справа на элементарную матрицу перестановок ![]() , получаем матрицу
, получаем матрицу ![]() .
.
В результате на необходимом нам месте оказывается ненулевой элемент ![]() , уже преобразованная часть матрицы не меняется, можно применять обычный шаг метода Данилевского к матрице
, уже преобразованная часть матрицы не меняется, можно применять обычный шаг метода Данилевского к матрице ![]() .
.
2.2 Рассмотрим второй нерегулярный случай, когда в матрице ![]() элемент
элемент ![]() и все элементы левее, тоже нулевые. В этом случае характеристический определитель матрицы
и все элементы левее, тоже нулевые. В этом случае характеристический определитель матрицы ![]() можно представить в виде
можно представить в виде
![]() где
где ![]() и
и ![]() - единичные матрицы соответствующей размерности, а квадратные матрицы
- единичные матрицы соответствующей размерности, а квадратные матрицы ![]() и
и ![]() имееют вид:
имееют вид: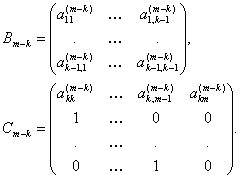
Обратим внимание на то, что матрица ![]() уже имеет нормальную форму Фробениуса, и поэтому сомножитель
уже имеет нормальную форму Фробениуса, и поэтому сомножитель ![]() просто развертывается в виде многочлена с коэффициентами, равными элементам первой строки.
просто развертывается в виде многочлена с коэффициентами, равными элементам первой строки.
Сомножитель ![]() нужно преобразовывать. Для
развертывания можно применять метод Данилевского, приводя матрицу
нужно преобразовывать. Для
развертывания можно применять метод Данилевского, приводя матрицу ![]() подобными преобразованиями к нормальной форме Фробениуса.
подобными преобразованиями к нормальной форме Фробениуса.
Указанный подход становится неудовлетворительным при вычислении собственных значений матриц, имеющих порядок m в несколько десятков (и тем более сотен). В частности, одним из недостатков является так же то, что точность вычисления корней многочлена высокой степени данным методом чрезвычайно чувствительна к погрешности (накапливающейся со скоростью геометрической прогрессии) в коэффициентах, и на этапе вычисления последних может быть в значительной степени потеряна информация о собственных значениях матрицы.
Тесты метода и ПО см. В Приложении Б.
Сходимость метода
Определение. Квадратная матрица Р порядка m называется подобной матрице А , если она представлена в виде ![]() , где S - невыродженная квадратная матрица порядка m.
, где S - невыродженная квадратная матрица порядка m.
Теорема. Характеристический определитель исходной и подобной матрицы совпадают .
Доказательство.
Идея метода Данилевского состоит в том, что матрица А подобным преобразованиям приводится, к так называемой нормальной форме Фробениуса
 .
.
Теорема. Пусть ![]() є есть собственное значение , а
є есть собственное значение , а ![]() есть соответствующий собственный вектор матрицы Р , которая подобна матрице А ,т.е.
есть соответствующий собственный вектор матрицы Р , которая подобна матрице А ,т.е. ![]()
Тогда ![]() есть собственный вектор матрицы А , соответствующий собственному значению
есть собственный вектор матрицы А , соответствующий собственному значению ![]()
Доказательство.Тривиально следует из того, что ![]()
Домножая левую и правую часть этого равенства слева на S , имеем
![]() А это и означает, что
А это и означает, что ![]() -собственный вектор матрицы А , отвечающий собственному значению
-собственный вектор матрицы А , отвечающий собственному значению ![]()
Описание входных и выходных данных
Входные параметры:
Квадратная матрица порядка n*n. Рекомендуется, чтобы она была хорошо обусловлена.
Выходные параметры:
Получаем коэффициенты при степенях ![]() характеристического полинома. Решая данное уравнение получаем собственные значения исходной матрицы. Следующим шагом является определение собственных векторов.
характеристического полинома. Решая данное уравнение получаем собственные значения исходной матрицы. Следующим шагом является определение собственных векторов.
.
Заключение
Обозначим некоторые выводы по проделанной работе:
Во время освоения данного метода мы не могли пропустить некоторые минусы метода Данилевского:
- Погрешность накапливается со скоростью геометрической прогрессии.
- Приходится решать достаточно сложное уравнение порядка n (если решать с помощью приближенных метод, снова получаем некоторую погрешность)
- В программном варианте используются достаточно большие объемы оперативной памяти, к примеру, приходится хранить до 4 матриц порядка n*n.
Но так же нельзя не остановиться на очевидных плюсах метода:
- Метод удобен для нахождения собственных векторов практически любой матрицы. Рекомендуется рассматривать матрицы меньше порядка нескольких десятков.
- Данный метод очень удобен в программировании (на этапе разработки ПО проблем практически не возникало).
В целом метод все-таки не рекомендуется для решения задач, требующих высоких точностей. Но из-за своей простоты, и высокой скорости, подходит для больших массивов, не требующих отсутствие погрешности.
Список литературы
1. Основы численных методов: Учебник для вузов/ В.М. Вержбицкий. – М.: Высш. Шк., 2002. – 840 с.: ил.
2. Высшая математика для экономистов: Учебник для вузов/ Н.Ш. Кремер, Б.А. Путко, И.М. Тришин, М.Н. Фридман; Под ред. проф. Н.Ш. Кремера. – 2-е изд., перераб. и доп. – М.: ЮНИТИ, 2004. – 471 с.
3. Интернет.
4. Библия Delphi/ М.Е. Фленов – СПб.: БХВ-Петербург, 2005. – 880 с.: ил.
Приложение А
unit MainUnit;
interface
uses
Windows, …, Buttons;
type
Matrix = array of array of real;
TForm1 = class(TForm)
…
private
{ Private declarations }
// Процедура "перестановки" матрицы, возвращает true если все хорошо
function Remove(Var rez: Matrix; i: integer): boolean;
// Умножение 2-х матриц
procedure Multiple(a,b:Matrix; Var rez: Matrix);
// Возвращение решений
function FindDet(Var a:Matrix):string;
// Обнуление матриц
procedure Zero(Var a:Matrix);
public
{ Public declarations }
end;
var Form1: TForm1;
implementation
{$R *.dfm}
function TForm1.FindDet(Var a: Matrix):string;
Var i,j : integer;
M,Mob,bac : Matrix;
flag : boolean;
begin
SetLength(M,Length(a[1]),Length(a[1]));
SetLength(Mob,Length(a[1]),Length(a[1]));
SetLength(bac,Length(a[1]),Length(a[1]));
flag:=true;
for i:=Length(a[1])-2 downto 0 do
// Построение матриц
BEGIN
// Обработка случая 2.1
if (a[i+1,i]=0) and (not Remove(a,i)) then
begin
// Если ничего не помогло
flag:=false;
Break;
end;
// Обнуление всех матриц
Zero(M); Zero(Mob); Zero(bac);
// Построение матриц М
for j:=0 to Length(a[i])-1 do
begin
Mob[j,j]:=1;
Mob[i,j]:=a[i+1,j];
M[j,j]:=1;
M[i,j]:=-Mob[i,j]/a[i+1,i];
if i=j then M[i,j]:=1/a[i+1,i];
end;
// Умножение матрицы А на М
Multiple(a,M,bac); // A*M
Multiple(Mob,bac,a); // M^(-1)*(A*M)
END;
// Обработка случая 2.2, если надо
if not flag then
begin
M:=nil;
Mob:=nil;
// Находим матрицу С и выводим ее коэффициенты
SetLength(bac,1,length(a)-i-1);
for j:=i+1 to length(a)-1 do bac[0,j-i-1]:=a[i,j]; // Матрица C
Result:='('+FloatToStrF(bac[0,0],ffFixed,10,3);
for i:=1 to Length(bac)-1 do
Result:=Result+','+FloatToStrF(bac[0,i],ffFixed,10,3);
Result:=Result+'),';
// "Урезаем" матрицу А до состояния B, см. 2.2 пункт алгоритма
SetLength(a,i+1,i+1);
// Вызываем рекурсивно процедуру
Result:=Result+FindDet(a);
end
else begin
Result:='('+FloatToStrF(a[0,0],ffFixed,10,3);
for i:=1 to Length(a)-1 do
Result:=Result+','+FloatToStrF(a[0,i],ffFixed,10,3);
Result:=Result+')';
end;
bac:=nil;
end;
procedure TForm1.bbPlusClick(Sender: TObject);
begin
sgInData.ColCount:=sgInData.ColCount+1;
sgInData.RowCount:=sgInData.RowCount+1;
if sgInData.ColCount=11 then ShowMessage('Attention!!! Полученные результаты имеют малую точность');
end;
procedure TForm1.bbMinusClick(Sender: TObject);
begin
if sgInData.ColCount<3 then Exit;
sgInData.ColCount:=sgInData.ColCount-1;
sgInData.RowCount:=sgInData.RowCount-1;
end;
procedure TForm1.bbOpenClick(Sender: TObject);
Var k : real;
f : textfile;
a,i,j : integer;
begin
OpenDialog1.Filter:='Все файлы (*.*)|*.*| Файлы .txt (*.txt)|*.TXT';
OpenDialog1.Title:='Выбор файла для этой проги';
OpenDialog1.FilterIndex:=2;
if OpenDialog1.Execute then
begin
AssignFile(f,OpenDialog1.FileName);
Reset(f);
end
else Exit;
ReadLn(f,a);
sgInData.ColCount:=a;
sgIndata.RowCount:=a;
for i:=0 to a-1 do
begin
for j:=0 to a-1 do
begin
Read(f,k);
sgIndata.Cells[j,i]:=FloattoStr(k);
end;
ReadLn(f);
end;
CloseFile(f);
end;
procedure TForm1.bbFindClick(Sender: TObject);
Var a :matrix;
i,j :integer;
begin
try
SetLength(a,sgInData.ColCount,sgInData.RowCount);
for i:=0 to sgInData.RowCount-1 do
for j:=0 to sgInData.RowCount-1 do a[i,j]:=StrToFloat(sgInData.Cells[j,i]);
except
begin
a:=nil;
ShowMessage('STOP! Неправильный ввод, проверьте входные данные');
Exit;
end;
end;
OutData.Clear;
OutData.Lines.Add('Коэффициенты характеристического уравнения');
OutData.Lines.Add(FindDet(a));
a:=nil;
end;
procedure TForm1.Multiple(a, b: Matrix; var rez: Matrix);
var i,k,j : word;
Begin
for i:=0 to Length(a[1])-1 do
for k:=0 to Length(a[1])-1 do
begin
// Обновление занятых матриц
rez[i,k]:=0;
for j:=0 to Length(a[1])-1 do rez[i,k]:=rez[i,k]+a[i,j]*b[j,k];
end;
end;
function TForm1.Remove(var rez: Matrix; i: integer): boolean;
Var j,k : integer;
E,bac : Matrix;
begin
Result:=false;
for k:=0 to i-1 do // Ищем ненулевой элемент слева
if rez[i+1,k]<>0 then
begin
Result:=true;
Break;
end;
if not Result then Exit;
SetLength(E,Length(rez[1]),Length(rez[1]));
SetLength(bac,Length(rez[1]),Length(rez[1]));
for j:=0 to Length(rez[1])-1 do E[j,j]:=1;
for j:=0 to Length(rez[1])-1 do
begin
// Меняем две строки местами в матрице E
E[i,j]:=-E[i,j]-E[k,j];
E[k,j]:=-E[i,j]-E[k,j];
E[i,j]:=-E[i,j]-E[k,j];
end;
Multiple(rez,E,bac); // A*M
Multiple(E,bac,rez); // M^(-1)*(A*M)
E:=nil;
bac:=nil;
end;
procedure TForm1.Zero(var a: Matrix);
Var i,j: integer;
begin
for i:=0 to Length(a)-1 do
for j:=0 to Length(a[0])-1 do a[i,j]:=0;
end;
end.
Приложение Б
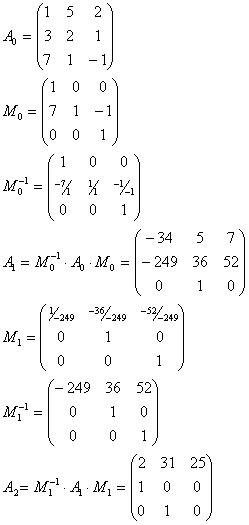
Результаты работы программы с теми же входными данными:
Рис 1.
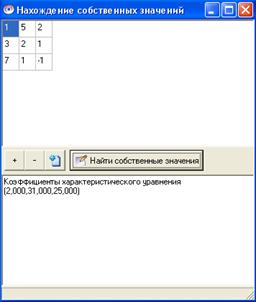
Приложение Б
(продолжение)
![]()
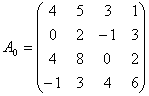
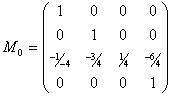
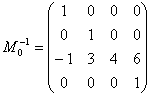
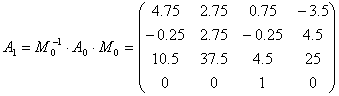
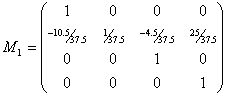

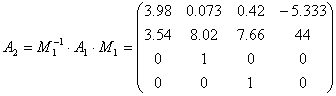
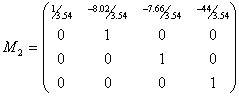

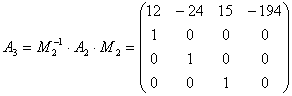
Результаты работы программы с теми же входными данными:
Рис 2.
Похожие работы
... собой, их взаимное дополнение друг другом. Недооценивая роль гипотез, как видно из приведенной цитаты Лапласа и из всего его практического творчества, он только отдавал дань духу времени. В области небесной механики Лаплас мог еще обходиться без гипотез, хотя в скрытой форме он должен был нередко ими пользоваться. Араго говорил, что ни один геометр не остерегался так решительно духа гипотез, как ...
... чиновником, а мате- матические трактаты публиковались рядом с текстами по чайной церемонии или искусству икебана. Может быть даже в большой степени, чем японская культура, японская наука является изначально старательной ученицей китайской. В 646 г. благодаря реформам Тайка (тайка (яп.)- великая перемена), осуществленным императором Котоку, Япония приняла государ- ственную модель ...


0 комментариев