Разработка модели теории массового обслуживания

Министерство информационных технологий и связи РФ

Сибирский государственный университет телекоммуникаций и информатики

Факультет информатики и вычислительной техники

Кафедра вычислительных систем

Курсовая работа

по курсу Моделирование

Выполнили: Степанов Е.Е.

Гордеев С.А.

Гомзяков А.В.

студенты гр.ВМ-37

Проверил: Рудых Я.И.

Новосибирск 2005

Содержание

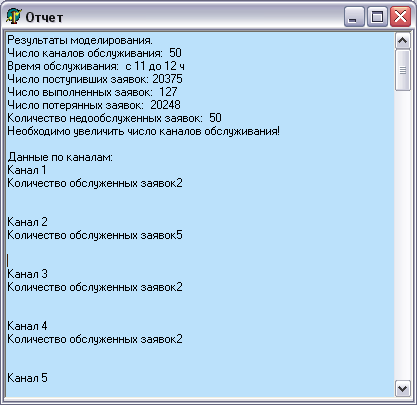
1.    Постановка задачи

2.    Описание модели в терминах PDEVS формализма

3.    Атомарные компоненты

4.    Полученные результаты

5.    Основные фрагменты кода

Вывод

1.         Постановка задачи

 

Модель состоит из трех обслуживающих серверов. Каждый сервер имеет очередь, в которой заявки могут ожидать своей очереди. Также есть генератор сообщений. Первая очередь бесконечная, остальные конечные. Обработки заявок всех серверов распределены экспоненциально. В начальный момент времени очереди. Необходимо построить модель в терминах PDEVS-формализма и произвести эксперименты над моделью с помощью пакета DEJaView.

Необходимо ответить на следующие вопросы:

1)         Выдать статистику по всем очередям.

2)         Максимальную длину первой очереди.

3)   Сколько процентов сообщений прошло через очередь без задержек - «сквозняки».

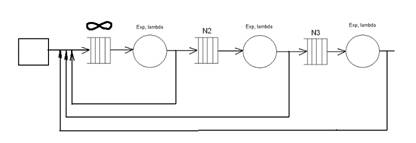
Рис. 1. Схематическое изображение модели

 

2.         Описание модели в терминах PDEVS формализма

В PDEVS-модели существует 7 компонент:

Queue1, Queue2 и Queue3 – это три очереди.

Server1, Server2 и Server3 – это три прибора (сервера). Время обслуживания распределено экспоненциально.

MessageGenerator - генератор сообщений.

Рассмотрим более подробно логику работы компонент.

1.  Генератор подает сообщение в очередь Queue1.

2. В начальный момент времени все серверы находятся в состоянии free (свободен). Cерверы Server1, Server2 посылают сообщение на очереди Queue2 и Queue3 соответственно, это говорит о готовности серверов принимать сообщения.

3.         Приняв сообщение каждая очередь подаёт сообщение на выход toNext и он приходит на вход fromPrev соответствующего каждой очереди сервера.

4.         Сервет меняет своё состояние с free (свободен) на busy (занят) и через некоторое время подаёт сообщение на выход toNext и после этого ждёт от следующей очереди подтверждения что в данной очереди ещё есть хотя бы одно место.

5.          После того как сервер отправил сообщение слёдующей очереди, он переходит в состояние free (свободен) и посылает предыдущей очереди сообщение, которое говорит о готовности сервера принимать следующее сообщение.

6.         Также существует возможность перехода сообщения с Серверов в очередь Queue1 с вероятностями P1, P2, P3.

3.Атомарные компоненты

 

Класс атомарной компоненты	Объекты класса атомарной компоненты	Возможные состояния компоненты	Входные порты	Выходные порты
Server1	Server1	Free, Busy	FromPrev,FromNext	ToPrev,toNext,Vozvrat
Server2	Server2	Free, Busy	FromPrev,FromNext	ToPrev,toNext,Vozvrat
Server3	Server3	Free, Busy	FromPrev,FromNext	ToPrev,Vozvrat
Queue1	Queue1	Free, Full	FromPrev,FromNext,Vozvrat	ToPrev,toNext
Queue2	Queue2	N=={1,2,3,4,5}	FromPrev,FromNext	ToPrev,toNext
Queue3	Queue3	N=={1,2,3,4,5}	FromPrev,FromNext	ToPrev,toNext

Алгоритмы функционирования компонент:

Компоненты классов Server1 и Server2:

 

Delta_int:

Остаемся в текущем состоянии

Delta_exp

Если (пришел новый пакет от очереди)

{

переходим в состояние “busy”

}

Lambda

Если(Сообщение от предыдущей очереди){

Если пакет обработан, то пытаемся отправить его следующей очереди.

Случайно определяем куда пойдёт сообщение – или в начало цепи, или в следующую очередь.

Отсылаем предыдущей очереди уведомление о том что сервер освободился.

}

Компоненты класса Queue2,Queue3:

 

Delta_int:

остаемся в текущем состоянии

Delta_exp

Если (пришёл новый пакет)

{

Если (Флаг ожидания, ожидания освобождения сервера)

{

Увеличиваем счётчик поступивших пакетов на 1

Так же выполняем действия необходимые для вычисления средней длины очереди

}

Иначе

Если (Очередь не ждёт освобождения сервера )

{

«Сквозняк»

Выполняем действия по вычислению доли сквозняков

}

Иначе

Если (пришло сообщение от сервера)

{

Флаг готовности сервера ставим в значение истина

}

Lambda

Если (пришёл новый пакет)

{

Если (Сервер свободен)

{

Отсылаем сообщение серверу

«Сквозняк»

Выполняем операции по вычислению доли сквозняков

}

Если (Ожидаем сервер)

{

Если очередь переполнилась посылаем сообщение серверу

}

}

Если (пришло сообщение от сервера)

{

Если(Очередь не пуста){

Посылаем пакет на порт toNext очереди

Уменьшаем длину очереди на 1

}

}

Компоненты классов Server3:

Delta_int:

Остаемся в текущем состоянии

Delta_exp

Если (пришел новый пакет от очереди)

{

переходим в состояние “busy”

}

Lambda

Если (сообщение от предыдущей очереди){

Если пакет обработан, то пытаемся отправить его следующей очереди.

Случайно определяем куда пойдёт сообщение – или в начало цепи, или на выход из цепи.

Отсылаем уведомление предыдущей очереди о том, что сервер освободился.

}

Компонент класса Queue1:

Delta_int:

остаемся в текущем состоянии

Delta_exp

Если (пришёл новый пакет(или из цепи, или из генератора сообщений))

{

Если (Флаг ожидания, ожидания освобождения сервера)

{

Увеличиваем счётчик поступивших пакетов на 1

Выполняем действия по нахождению макс максимальной длины очереди

}

Иначе

Если (Сервер свободен )

{

«Сквозняк»

Выполняем действия по вычислению доли сквозняков

}

Иначе

Если (пришло сообщение от сервера)

{

Флаг готовности сервера ставим в значение истина

}

Lambda

Если( пришёл новый пакет(из генератора или из цепи) )

{

Если (Сервер свободен)

{

Отсылаем сообщение серверу

«Сквозняк»

Выполняем операции по вычислению доли сквозняков

}

Если (Ожидаем сервер)

{

}

}

Если (пришло сообщение от сервера)

{

Если(Очередь не пуста){

Посылаем пакет на порт toNext очереди

Уменьшаем длину очереди на 1

Выполняем действия по вычислению максимальной длины очереди

}

}

Компонент класса: MessageGenerator.

Если(пришло системное сообщение)

{

Отправляем сообщение первой очереди

Увеличиваем число сгенерированных сообщений на 1

}