Алгоритмизация задачи

3. Алгоритмизация задачи

В соответствии с постановленной в разделе 2 задачей целесообразно реализовать алгоритм, использующий обращение к соответствующим подпрограммам из головной программы.

Алгоритм работы головной программы следующий:

Скрыть курсор с использованием подпрограммы - процедуры скрытия курсора и вывести в специальном окне заставку программы, содержащую сведения о назначении программы, исполнителе и руководителе курсовой работы, а также подсказку для пользователя о последующих действиях, с использованием подпрограммы - процедуры заставки.

Запустить подпрограмму-процедуру вертикального меню при нажатии любой клавиши с использованием подпрограмм-процедур построения окна, вывода рамки окна и скрытия курсора.

Запустить подпрограмму-процедуру справки и вывести в специальном окне справочные сведения о работе с программой при выборе пункта меню «Справка» с использованием строки-подсказки о возврате в меню.

Запустить подпрограмму-процедуру поиска решения системы дифференциальных уравнений методом Рунге-Кутта при выборе пункта меню «Метод Рунге-Кутта» с использованием включения курсора, а также строки-подсказки о возврате в меню.

Запустить подпрограмму-процедуру поиска решения системы дифференциальных уравнений методом Рунге-Кутта-Мерсона при выборе пункта меню «Метод Рунге-Кутта-Мерсона» с использованием включения курсора, а также строки-подсказки о возврате в меню.

Завершить работу программы при выборе пункта меню «Выход».

Алгоритм поиска решения системы уравнения методом Рунге-Кутта в подпрограмме-процедуре runkut включает следующие шаги:

Создать окно для ввода исходных данных и вывода результатов вычисления.

Восстановить отображение курсора нормального размера соответствующей подпрограммой - процедурой.

Задать начальный шаг-h и начальные значение x_о,y₁₀,…,y_N0 .

В подпрограмме-функции задаём вид правой части уравнений.

В подпрограмме-процедуре задаём вид системы дифференциальных уравнений.

Организовать цикл для поиска коэффициентов погрешности по формулам (2-5)

По формуле (6) найти решение системы дифференциальных уравнений.

Вывести результаты вычислений в том же окне.

Вывести в окне запрос о продолжении вычислений с новыми исходными данными.

Выполнить анализ кода нажатой в ответ на запрос клавиши: при нажатии “Y” повторить ввод снова, при нажатии “N” перейти в окно с меню.

Алгоритм поиска решения системы уравнений методом Рунге-Кутта-Мерсона в подпрограмме процедуре rukutm включает:

Создание окно для ввода исходных данных и вывода результатов вычисления.

Восстановления отображение курсора нормального размера соответствующей подпрограммой - процедурой.

Задание начального шаг-h, начальных значений x_о,y₁₀,…,y_N0 и точности вычисления- ε.

Подпрограмме-процедуре задаём вид системы дифференциальных уравнений

В подпрограмме-функции задаём вид правой части уравнений

С помощью пяти циклов с управляющей переменной J=1,N вычисляем коэффициенты по формулам (7)-(11).

В последнем цикле находим решение системы дифференциальных уравнений по формуле (12) и погрешность по формуле (13).

Проверка выполнение условий (14) и (15). Если первое условие не выполняется то h:=h/2 и переходим к п.5.

Если выполняются оба условия, то значение x_i+1=x_i+h и Y_j(i+1) выводим на экран.

Если второе условие не выполняется, то h:=h+h и переходим к п.5.

Вывести результаты вычислений в том же окне.

Вывести в окне запрос о продолжении вычислений с новыми исходными данными.

Выполнить анализ кода нажатой в ответ на запрос клавиши: при нажатии “Y” пoвторить ввод снова , при нажатии “N” перейти в окно с меню.

4. Идентификаторы программы

 

Для указания соответствия обозначений переменных в формулах математической формулировки и их идентификаторов в программе сведем их в таблицу 1:

Таблица 1

Обозначение параметров		Смысл параметра
В формулах	В программе
Y1…Yn	Y[1]…Y[n]	Начальные приближения
ε	E	Точность результата
h	H	Шаг интегрирования
Кij	K[j]	Коэффициенты погрешности
N	n	Количество уравнений
	F[1]	Первое уравнение системы
	F[2]	Второе уравнение системы

Остальные идентификаторы являются промежуточными или служебными.

5. Блок-схема алгоритма

 

5.1 Блок-схема алгоритма головной программы

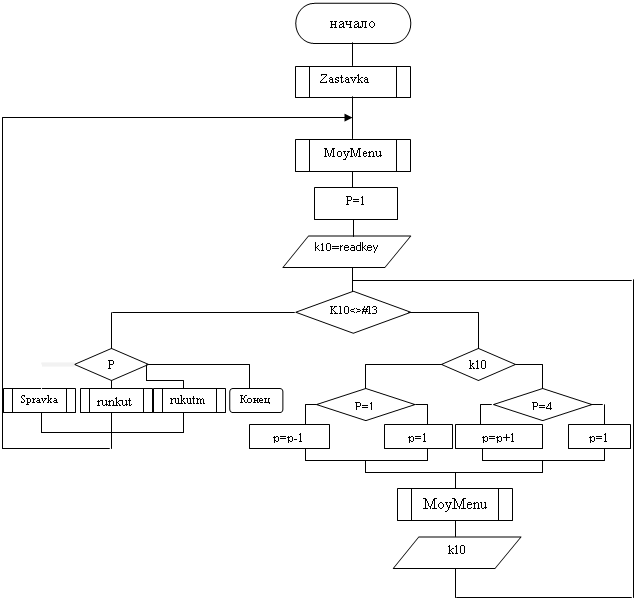
Нет Да

#72 #80

Да Нет Да Нет