Z – располагаемое количество ресурса

1.         z – располагаемое количество ресурса,

2.         n – мера квантования z

3.        

4.        

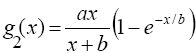
5.        

Искомые параметры

1.          f_N (z) = f_N (nΔ ) - искомый максимум функции R

2.          x_N (z) – искомое оптимальное количество ресурса

МЕТОД РЕШЕНИЯ

Переходя к изложению вычислительной схемы решения задачи с применением основного функционального уравнения (1.15), предположим (а это существенно для дальнейшего изложения), что переменные задачи N i xi , ... 2, 1, , = , а также количества распределяемого ресурса как в (1.10), так и в (1.15) могут принимать только дискретные значения с некоторым выбранным шагом Δ >0. То есть имеет место:

где nΔ = z . Соответственно, функции (1.10) в рекуррентном соотношении (1.15) будут вычисляться только для указанных в (1.16) значений  или, что то же самое, только для таких точек:

Указанный подход позволяет избежать процедуры интерполирования при вычислении значений , исходя из вычисленных значений fm−1( y) в точках y = 0, Δ , 2Δ , ... , z . Действительно, для вычисления под знаком максимума в (1.15) значения  − интерполирования не требуется, так как здесь с учетом (1.16) и (1.17) имеет место: .

Согласно (1.15), для вычисления  вначале следует найти значения  для всех значений  из (1.16) с помощью соотношений (1.12)

или (1.13), которые доставляют множество всех требуемых значений

. Затем для всех  (1.16) с учетом (1.15) вычисляются значения:

где.Процедура максимизации (1.18) заключается в том, чтобы вначале для каждого z ~ последовательно вычислить значения:   а затем выбрать из них максимальное, то есть искомое значение ; при этом определяется и соответствующее ему оптимальное значение .

Получив множество значений для , можно приступить к вычислению функции исходя из (1.15) при m =3:

и т.д. для остальных m = 4, 5, ... , N .

Таким образом, в процессе решения уравнения (1.15) для m = 2, 3, ... , N

последовательно заполняется таблица, подобная табл. 1.1.

Таблица 1.1

Оптимальные доходы в зависимости от количества процессов

и выделенного ресурса

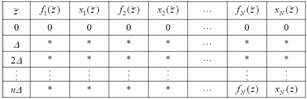
С заполнением последних двух столбцов указанной таблицы решение

задачи фактически получено. Действительно, поскольку функция  по построению монотонно неубывающая по  , постольку fN (z) = fN (nΔ ) - искомый максимум функции R (1.1), а xN (z) – искомое оптимальное количество ресурса, выделенное для N-го процесса. Стало быть, оставшееся количество ресурса, равное z − xN (z) , должно быть распределено оптимальным образом между остальными процессами. Соответствующее решение, то есть оптимальный доход (1.10) для первых N −1 процессов, находится в столбце с заголовком  − , а именно: в строке, отвечающей значению . В этой же строке в столбце с заголовком  − находится величина оптимального количества ресурса, который выделяется для (N −1)-го процесса. Таким образом, перемещаясь по столбцам табл. 1.1 справа налево (это т.н. обратный ход [1, 3]), можно последовательно определить все значения  , которые доставляют абсолютный максимум функции R(x1, x2 , ... , xN ) (1.1) в области (1.2), (1.3) для заданного количества распределяемого ресурса – z, конечно же, с учетом дополнительных ограничений (1.16), (1.17)

  ОБОСНОВАНИЕ ВЫБОРА ПРОГРАММНЫХ СРЕДСТВ

Курсовая работа выполнена с помощью программы Microsoft Office Excel, одной из наиболее передовых, мощных и современных сред разработки Windows-приложений и электронных таблиц. Встроенное средство поиска решений позволяет быстро справиться с задачей о распределения ресурсов.

ОПИСАНИЕ ИНТЕРФЕЙСА ПОЛЬЗОВАТЕЛЯ

Для начала работы с программой следует задать n и z и нажать кнопку определить

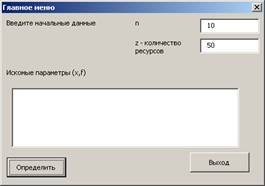
После этого программа создаст таблицы.

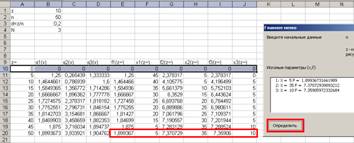
СПИСОК ЛИТЕРАТУРЫ

1. Беллман, Р. Прикладные задачи динамического программирования /Р. Беллман, С. Дрейфус. – М.: Наука, 1965. – 460 с.

2. Ланкастер, К. Математическая экономика / К. Ланкастер. – М.: Советское радио, 1972. – 464 с.

3. Колемаев, В.А. Математическая экономика / В.А. Колемаев. – М.:

ЮНИТИ, 1998. – 240 с.

4. Беллман, Р. Процессы регулирования с адаптацией / Р. Беллман. – М.: Наука, 1964. – 360 с.

5. Первозванский, А.А. Математические модели в управлении производством / А.А. Первозванский. – М.: Наука, 1975. – 616 с.

6. Калихман, И.Л. Динамическое программирование в примерах и задачах / И. Л. Калихман, М. А. Войтенко. – М.: Высшая школа, 1979. – 125 с.
ТЕКСТ ПРОГРАММЫ

Public Function f_g1(x As Double) As Double

f_g1 = 2.5 * Sqr(x) / (Sqr(x) + 1)

End Function

Public Function f_g2(x As Double) As Double

f_g2 = 6 * x * (1 - Exp(-x / 4)) / (x + 4)

End Function

Public Function f_g3(x As Double) As Double

f_g3 = 2 * x / (x + 0.5)

End Function

Private Sub CommandButton1_Click()

Dim i As Integer

Dim n As Integer

Dim z As Double

Dim d As Double

Dim m_str As String

 Range("A1").Select

 n = Val(TextBox1.Text)

 z = Val(TextBox2.Text)

 d = z / n

 ActiveCell.Cells(1, 2) = n

 ActiveCell.Cells(2, 2) = z

 Range("A11").Select

 For i = 1 To 100

For j = 1 To 10

ActiveCell.Cells(i, j) = ""

Next

 Next

 For i = 1 To 10

ActiveCell.Cells(0, i) = 0

 Next

 For i = 1 To n

ActiveCell.Cells(i, 1) = i * d

ActiveCell.Cells(i, 2) = f_g1(i + 0#)

ActiveCell.Cells(i, 3) = f_g2(i + 0#)

ActiveCell.Cells(i, 4) = f_g3(i + 0#)

ActiveCell.Cells(i, 5) = f_g1(i + 0#)

 Next

 For i = 1 To n

ActiveCell.Cells(i + 0, 7) = GetF2Val(i + 0, d)

ActiveCell.Cells(i + 0, 8) = Int(GetF2Pos(i + 0, d) * d)

ActiveCell.Cells(i + 0, 9) = GetF3Val(i + 0, d)

ActiveCell.Cells(i + 0, 10) = Int(GetF3Pos(i + 0, d) * d)

ActiveCell.Cells(i + 0, 6) = Abs(z - ActiveCell.Cells(i + 0, 8) - ActiveCell.Cells(i + 0, 10))

 Next

 ListBox1.Clear

 

 For i = 1 To 3

m_str = Str(i) + ": X = " + Str(ActiveCell.Cells(n + 0, 4 + i * 2)) + " F = " + Str(ActiveCell.Cells(n + 0, 3 + i * 2))

ListBox1.AddItem (m_str)

 Next

 Range("A10:J10").Select

End Sub

Private Sub CommandButton2_Click()

Hide

End Sub

Public Function GetF2Val(n As Integer, d As Double) As Double

 Dim maxs As Double

 maxs = f_g2(0) + f_g1(n * d)

 For i = 1 To n

If f_g2(i * d) + f_g1((n - i) * d) >= maxs Then

maxs = f_g2(i * d) + f_g1((n - i) * d)

End If

 Next

 GetF2Val = maxs

End Function

Public Function GetF2Pos(n As Integer, d As Double) As Integer

 Dim maxs As Double

 Dim maxp As Integer

 Range("A11").Select

 maxs = f_g2(0) + f_g1(n * d)

 max_p = 0

 For i = 1 To n

If f_g2(i * d) + f_g1((n - i) * d) >= maxs Then

maxs = f_g2(i * d) + f_g1((n - i) * d)

maxp = i

End If

 Next

 GetF2Pos = maxp

End Function

Public Function GetF3Val(n As Integer, d As Double) As Double

 Dim maxs As Double

 maxs = f_g3(0) + f_g2(n * d)

 For i = 1 To n

If f_g3(i * d) + f_g2((n - i) * d) >= maxs Then

maxs = f_g3(i * d) + f_g2((n - i) * d)

End If

 Next

 GetF3Val = maxs

End Function

Public Function GetF3Pos(n As Integer, d As Double) As Integer

 Dim maxs As Double

 Dim maxp As Integer

 Range("A11").Select

 maxs = f_g3(0) + f_g2(n * d)

 max_p = 0

 For i = 1 To n

If f_g3(i * d) + f_g2((n - i) * d) >= maxs Then

maxs = f_g3(i * d) + f_g2((n - i) * d)

maxp = i

End If

 Next

 GetF3Pos = maxp

End Function