Нахождение оптимального решения в системе Mathcad

2. Нахождение оптимального решения в системе Mathcad.

Введем обозначения:

Суда первого типа – s.

Суда второго типа – n.

Прибыль от реализации всей продукции – P.

 

Mathcad получил результат:

Судов первого типа – 4 штуки, судов второго типа – 2 штуки.

Прибыль составляет 140000000 руб. Совпадает с результатом решения оптимизатора Excel.

Построение таблицы полученных решений.

 

№	План найденный вручную	План, найденный программным путем
	1	Excel	Mathcad
Прибыль, руб.	70000000	140000000	140000000

 

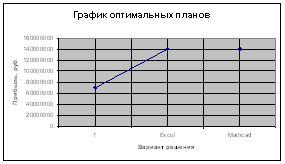
Вывод:

Наибольшая прибыль от реализации продукции получается при решении с помощью программы оптимизатора в Excel и в системе Mathcad.

Анализ оптимального плана и решение менеджера.

Оптимальными планами являются решения, полученные с помощью программ Excel и Mathcad, которые получили одинаковый результат:

Судна первого типа – 4 штуки, судов второго типа – 2 штуки. Прибыль будет составлять 140000000 руб.

При нахождении оптимального плана пассажировместимость остается прежней, равной 10000 человек. Для дальнейшего увеличения прибыли целесообразно увеличить пассажировместимость. Также остается неиспользованными 4600 тонн горючего и не задействованными 400 человек экипажа. В результате заморожены оборотные средства, оборотный капитал, увеличиваются расходы по хранению горючего на складе и не занятости экипажа, теряется прибыль. Завоз горючего можно сократить, а незанятое количество экипажа уволить.

Задача №3 (билет №59 ТВ).

 

Транспортная задача.

Определение проблемы: В современных условиях большие транспортные расходы связаны:

- с простоями в ожидании погрузочно-разгрузочных работ;

- с нерациональными перевозками;

- с затратами на бензин;

- с порожними пробегами и т. д.

В связи с этим необходимо решать задачи оптимального планирования перевозок грузов из пунктов отправления в пункты назначения.

Оптимизировать план перевозок груза можно по какому-либо экономическому показателю:

- финансовые затраты на перевозку грузов;

- время, затрачиваемое на перевозку.

Для решения таких задач в линейном программировании разработаны следующие методы:

- Симплекс-метод;

- Метод потенциалов;

- Венгерский метод.

Постановка транспортной задачи: В общем случае заключается в том, что нужно доставить необходимое количество ресурсов от разных поставщиков к разным потребителям. При этом:

- затраты на транспортировку ресурсов должны быть минимальными;

- возможности поставщиков ограничены;

- нужно полностью выполнить заявки каждого потребителя.

Построение экономико-математической модели задачи:

1. Имеются m пунктов отправления (поставщиков грузов),

А₁, А₂, А₃ …А_i, …А_m

на которых сосредоточены запасы како-либо груза в объемах соответственно:

а₁, а₂, а₃ …а_i, …а_m

где величина а_i – максимально возможное количество груза в i пункте отправления. Тогда суммарный запас груза у всех поставщиков составляет:

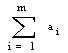
2. Имеются n пунктов назначения,

B₁, B₂, B₃ …B_j, …B_n

которые подали заявки на поставку грузов в объемах соответственно:

b₁, b₂, b₃, …b_j, …b_n

тогда суммарная величина заявок составляет:

3. Стоимость перевозки 1 единицы груза от поставщика А_i к потребителю B_j обозначим c_i,j (транспортный тариф).

Общая стоимость перевозок составляет матрицу транспортных издержек С.

Критерием оптимальности выберем суммарные затраты (издержки по перевозки груза).

Все исходные данные транспортной задачи записываются в виде таблицы (транспортной), в которой x_i,j – значение объема перевозки грузов от поставщика А_i к потребителю B_j.

Пункты отправления	Пункты назначения				Запасы аi
	В1	В2	…Вj...	Вn
А1	c11 x11	c12 x12	c1j x1j	c1n x1n	а1
А2	c21 x21	c22 x22	c2j x2j	c2n x2n	а2
…Аi…	ci1 xi1	ci2 xi2	cij xij	cin xin	аi
Аm	cm1 xm1	cm2 xm2	cmj xmj	cmn Xmn	аm
Заявки bj	b1	b2	bj	bn

Задача заключается в определении плана перевозок матрицы x, где

x (i = 1, m; j = 1, n ),

который удовлетворяет следующим условиям:

1. План перевозок от i поставщика всем потребителям (сумма по строке), ограничивается запасом на складе j поставщика.

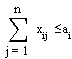
2. План поставок j потребителю от всех поставщиков (сумма по столбцу) должен быть не меньше объема заявок j потребителя.

3. Из физического смысла задачи определяем, что объемы перевозок x_ij не могут быть отрицательными.

x_ij≥ b_j; j = 1, n

4. Затраты на перевозку равны:

_{m n}

P(X) = ∑∑ c_ij* x_ij

^{i=1 j=1}

X – план перевозок, то есть матрица X.

Таким образом, экономико-математическая модель задачи можно записать в виде:

- Найти минимальное значение целевой функции:

_mn

P(X) = ∑∑ c_ij* x_ijmin

^{i=1 j=1}

Данная экономико-математическая модель является одной из разновидностей транспортной задачи.

Условие: требуется минимизировать затраты на перевозку грузов от заводов поставщиков (А1, А2, А3) на торговые склады В1, В2, В3. Товары могут доставляться с любого завода на любой склад, при условии:

1.         Минимальное количество поставляемого груза с завода А1 и завода А2 к каждому потребителю составляет 160 тонн.

2.         С завода А2 на склад В1 нужно привезти не более 200 тонн груза, а с завода А3 на склад В1 – не менее 100 тонн.

Необходимо учесть:

- возможности поставщиков;

- максимально удовлетворить заявки склада.

Дано:

1. Потребности склада:

В1 – 500;

В2 – 600;

В3 – 400.

2. Мощность заводов:

А1 – 500;

А2 – 600;

А3 – 500.

3. Стоимость перевозки единицы груза:

Потребители	В1	В2	В3
Поставщики
А1	9	6	2
А2	4	15	15
А3	17	7	8

Ручной поиск оптимального плана.

 

Цель: составить оптимальный план вручную

Используя стандартный программный пакет Excel, необходимо интуитивно задать пять возможных вариантов плана перевозки, я нашла наилучший интуитивный план перевозок продукции, при котором затраты на перевозку были минимальные.

Стоимость перевозки единицы груза от завода к складу.
Потребитель
Поставщик	В1	В2	В3
А1	9	6	2
А2	4	15	15
А3	17	7	8
План перевозок от завода к складу
Потребитель				План поставок	Мощность завода
Поставщик	В1	В2	В3
А1	180	160	160	500	500
А2	160	180	160	500	600
А3	160	260	80	500	500
Поставлено по складу	500	600	400
Потребность складов	500	600	400
Стоимость перевозок по каждому складу				Трансп. расходы
	4980	5480	3360	13820
Стоимость перевозки единицы груза от завода к складу.
Потребитель
Поставщик	В1	В2	В3
А1	9	6	2
А2	4	15	15
А3	17	7	8
План перевозок от завода к складу
Потребитель				План поставок	Мощность завода
Поставщик	В1	В2	В3
А1	180	160	160	500	500
А2	180	160	160	500	600
А3	140	280	80	500	500
Поставлено по складу	500	600	400
Потребность складов	500	600	400
Стоимость перевозок по каждому складу				Трансп. расходы
	4720	5320	3360	13400
Стоимость перевозки единицы груза от завода к складу.
Потребитель
Поставщик	В1	В2	В3
А1	9	6	2
А2	4	15	15
А3	17	7	8
План перевозок от завода к складу
Потребитель				План поставок	Мощность завода
Поставщик	В1	В2	В3
А1	180	160	160	500	500
А2	160	200	160	520	600
А3	160	140	80	380	500
Поставлено по складу	500	500	400
Потребность складов	500	600	400
Стоимость перевозок по каждому складу				Трансп. расходы
	4980	4940	3360	13280
Стоимость перевозки единицы груза от завода к складу.
Потребитель
Поставщик	В1	В2	В3
А1	9	6	2
А2	4	15	15
А3	17	7	8
План перевозок от завода к складу
Потребитель				План поставок	Мощность завода
Поставщик	В1	В2	В3
А1	160	160	160	480	500
А2	160	160	160	480	600
А3	180	270	80	530	500
Поставлено по складу	500	590	400
Потребность складов	500	600	400
Стоимость перевозок по каждому складу				Трансп. расходы
	5140	5250	3360	13750
Стоимость перевозки единицы груза от завода к складу.
Потребитель
Поставщик	В1	В2	В3
А1	9	6	2
А2	4	15	15
А3	17	7	8
План перевозок от завода к складу
Потребитель				План поставок	Мощность завода
Поставщик	В1	В2	В3
А1	170	170	160	500	500
А2	170	170	170	510	600
А3	160	260	70	490	500
Поставлено по складу	500	600	400
Потребность складов	500	600	400
Стоимость перевозок по каждому складу				Трансп. расходы
	4930	5390	3430	13750

Вывод:

Наилучшим планом из составленных вручную с помощью программы Excel является план №3, т.к. при данном плане затраты на перевозку минимальные и составляют 13280 руб.

Программный поиск оптимального решения.