Навигация
7. Найти экстремумы функции.
Из пункта 6 следует, что точка ![]() является критической, т. е экстремумом. Причем,
является критической, т. е экстремумом. Причем, ![]() - точка минимума.
- точка минимума.
Найдем значение функции в критической точке:
![]()
8. Найти точки перегиба функции.
Для этого найдем вторую производную от заданной функции:
![]()
![]()
Производная второго порядка, целое постоянное число, значит, точек перегиба функция не имеет.
Таким образом, получим, что при объеме производства ![]() средние издержки будут минимальными.
средние издержки будут минимальными.
Построение графика искомой функции средствами MS Excel
Для построения графика необходимо составить таблицу значений переменной и функции. Воспользуемся приложением MS Excel:
Таблица значений
| Расстояние от ближайшей точки на шоссе до искомой | Расстояние от искомой точки на шоссе до населённого пункта | Расстояние от буровой до искомой точки на шоссе по полю | Время движения курьера по полю | Время движения курьера по шоссе | Общее время в пути |
| 0 | 15 | 9 | 1,125 | 1,5 | 2,625 |
| 0,5 | 14,5 | 9,013878189 | 1,126734774 | 1,45 | 2,576734774 |
| 1 | 14 | 9,055385138 | 1,131923142 | 1,4 | 2,531923142 |
| 1,5 | 13,5 | 9,124143795 | 1,140517974 | 1,35 | 2,490517974 |
| 2 | 13 | 9,219544457 | 1,152443057 | 1,3 | 2,452443057 |
| 2,5 | 12,5 | 9,340770846 | 1,167596356 | 1,25 | 2,417596356 |
| 3 | 12 | 9,486832981 | 1,185854123 | 1,2 | 2,385854123 |
| 3,5 | 11,5 | 9,656603958 | 1, 207075495 | 1,15 | 2,357075495 |
| 4 | 11 | 9,848857802 | 1,231107225 | 1,1 | 2,331107225 |
| 4,5 | 10,5 | 10,0623059 | 1,257788237 | 1,05 | 2,307788237 |
| 5 | 10 | 10,29563014 | 1,286953768 | 1 | 2,286953768 |
| 5,5 | 9,5 | 10,54751155 | 1,318438944 | 0,95 | 2,268438944 |
| 6 | 9 | 10,81665383 | 1,352081728 | 0,9 | 2,252081728 |
| 6,5 | 8,5 | 11,10180166 | 1,387725207 | 0,85 | 2,237725207 |
| 7 | 8 | 11,40175425 | 1,425219281 | 0,8 | 2,225219281 |
| 7,5 | 7,5 | 11,71537451 | 1,464421814 | 0,75 | 2,214421814 |
| 8 | 7 | 12,04159458 | 1,505199322 | 0,7 | 2, 205199322 |
| 8,5 | 6,5 | 12,3794184 | 1,5474273 | 0,65 | 2, 1974273 |
| 9 | 6 | 12,72792206 | 1,590990258 | 0,6 | 2, 190990258 |
| 9,5 | 5,5 | 13,08625233 | 1,635781541 | 0,55 | 2,185781541 |
| 10 | 5 | 13,45362405 | 1,681703006 | 0,5 | 2,181703006 |
| 10,5 | 4,5 | 13,82931669 | 1,728664586 | 0,45 | 2,178664586 |
| 11 | 4 | 14,2126704 | 1,7765838 | 0,4 | 2,1765838 |
| 11,5 | 3,5 | 14,60308187 | 1,825385233 | 0,35 | 2,175385233 |
| 12 | 3 | 15 | 1,875 | 0,3 | 2,175 |
| 12,5 | 2,5 | 15,4029218 | 1,925365225 | 0,25 | 2,175365225 |
| 13 | 2 | 15,8113883 | 1,976423538 | 0,2 | 2,176423538 |
| 13,5 | 1,5 | 16,22498074 | 2,028122592 | 0,15 | 2,178122592 |
| 14 | 1 | 16,64331698 | 2,080414622 | 0,1 | 2,180414622 |
| 14,5 | 0,5 | 17,06604817 | 2,133256021 | 0,05 | 2,183256021 |
| 15 | 0 | 17,49285568 | 2,186606961 | 0 | 2,186606961 |
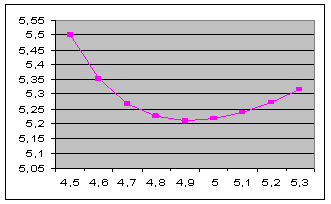
На основании таблицы строим график функции:

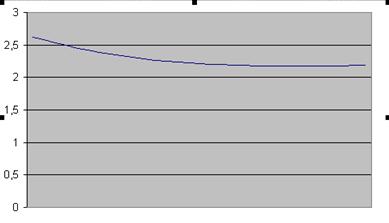
Найдем максимальное и минимальное значения. Для этого воспользуемся сортировкой.
| минимум | 2,175 |
| максимум | 2,625 |
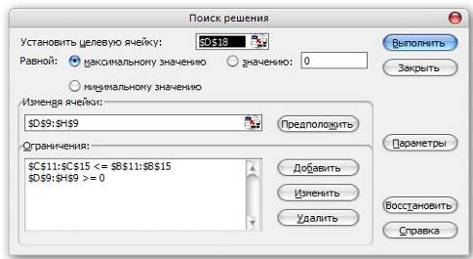
Решим задачу, пользуясь надстройкой "поиск решения". Выполним следующие действия:
1. Введем в любую ячейку целевую функцию
![]()
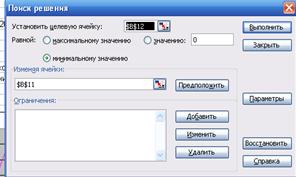
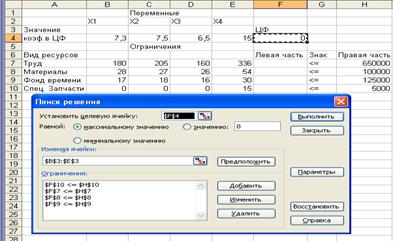
2. В меню Сервис выберем команду Поиск решения.
В появившемся окне уже установлена целевая ячейка.
Отмечаем флажок в поле "равной" на "минимальному значению", т.к наша функция стремится к минимуму.
В поле "Изменяя ячейки" выбираем любую ячейку с заранее введенной единицей.
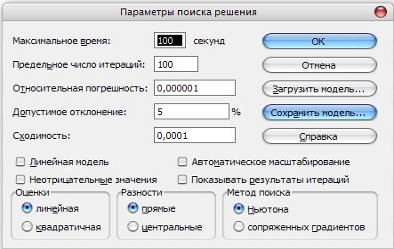
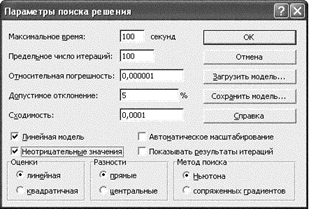
Нажимаем кнопку "выполнить", не меняя параметров.
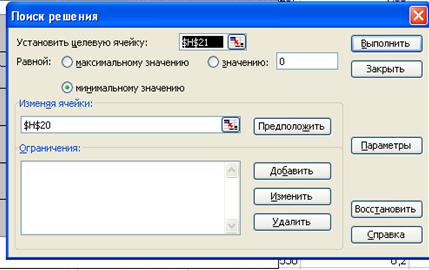
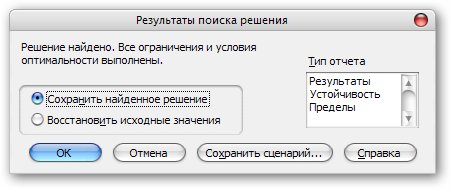
3. Просматриваем полученный результат.
| х = | 3 | |
| 2,175 | ||
Т. е. курьер должен двигаться в точку, удаленную на 3км от населенного пункта и на 12 км от ближайшей к буровой точке шоссе.
Вывод
В данной работе выполнены все поставленные цели и задачи. В ходе выполнения были сделаны следующие выводы.
Решив данную задачу, двумя способами, мы получили практически равные результаты.
В первом случае, в процессе решения задачи самостоятельно, мы потеряли достаточное количество времени, сохраняя большой риск ошибки в вычислениях.
Во втором же, решение задачи с помощью MS Excel, мы достигли того же результата минимизируя недостатки за считанные минуты.
Во время всеобщей компьютеризации, все пытаются облегчить себе процесс работы, и это действительно работает.
Используемая литература
1. Бурдюкова Е.В. Основы работы в Microsoft Excel. Хабаровск: ХК ИППК ПК, 2003.
2. Журнал "Информатика и образование" № 12, 2007.
3. Журнал "Информатика и образование" № 4, 2008.
4. Письменный Д.Т. Конспект лекций по высшей математике. М.: Айрис-пресс, 2007.
5. Практические задания и методические рекомендации по использованию информационных технологий. Хабаровск: ХК ИППК ПК, 2003.
Похожие работы
... все поставленные цели и задачи. В ходе выполнения были сделаны следующие выводы. Решив данную задачу, двумя способами, мы получили равные результаты. В первом случае, в процессе решения задачи самостоятельно, мы потеряли достаточное количество времени, сохраняя большой риск ошибки в вычислениях. Во втором же, решение задачи с помощью MS Excel, мы достигли того же результата минимизируя
... 0 505/103 0 792/103 669/103 500/103 Анализ Таблицы 6 позволяет сделать вывод о допустимости и оптимальности базиса XБ4=(x5, x7, x1, x2, x4)T. 3.4 Результат решения задачи планирования производства В результате решения поставленной задачи симплекс-методом получили набор производимой продукции x=(x1, x2, x3, x4, x5)=( 15145/103, 8910/103, 0, 1250/103, 3255/103), который удовлетворяет всем ...
... в больших объемах потребляет разнообразные запасные части для поддержания активной части своих производственных фондов в работоспособном состоянии. Запасные части для предприятий железнодорожного транспорта изготавливаются на заводах по ремонту подвижного состава и производству запасных частей и других специализированных предприятиях. Снижение издержек, связанных с обеспечением предприятий ...
... с помощью программы оптимизатора в Excel и в системе Mathcad. Анализ оптимального плана и решение менеджера. Оптимальными планами являются решения, полученные с помощью программ Excel и Mathcad, которые получили одинаковый результат: Судна первого типа – 4 штуки, судов второго типа – 2 штуки. Прибыль будет составлять 140000000 руб. При нахождении оптимального плана пассажировместимость ...
0 комментариев