Отчёт
о выполнении лабораторной работы № 5(2 часть)
"Решение систем линейных алгебраических уравнений (прямые методы)"
студентки группы 2Н14 физического факультета
Дмитриевой Ирины Георгиевны
Март 2010 г.
Задание 1. Привести систему уравнений к итерационному виду.
Решение:
Имеем систему:
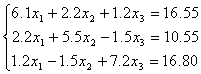
Приведем ее к итерационному виду. Для этого поделим каждое уравнение на соответствующий диагональный элемент, мы можем так сделать, потому что диагональные элементы не равны нулю. После деления на соответствующий диагональный элемент каждое уравнение из первого уравнения системы выражаем ![]() , из второго -
, из второго -![]() , из третьего, соответственно,-
, из третьего, соответственно,-![]() . Получаем эквивалентную систему исходной:
. Получаем эквивалентную систему исходной:
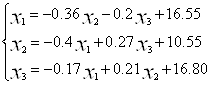
Эта система является системой приведенной к итерационному виду.
Задание 2. Проверить выполнение условия сходимости итерационного метода.Решение:
Проверим нашу систему на сходимость. Это проверяется следующими тремя условиями:
1. ![]()
2. ![]()
3. 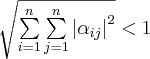
Для этого я воспользуюсь одним из условий сходимости для метода простой итерации, например, третьим, которое говорит о том, что сумма квадратов всех коэффициентов при неизвестных в правой части системы должна быть меньше единицы.
Оно записывается в следующем виде:
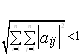
Проведем соответствующие вычисления:
![]()
Из проделанных вычислений можно сделать вывод, что наша система является сходящейся.
Задание 3. Составить программу на языке С++ для решения приведенной системы с заданной тонностьюРешение:
Для реализации метода простой итерации нам для начала необходимо проверить нашу систему на выполнение условия сходимости.
Проверяем ее мы с помощью условия:
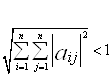
Если это условие сходимости по евклидовой метрике выполняется, то мы можем приступать к дальнейшей реализации метода простой итерации. Далее мы оцениваем точность нашего метода. Она оценивается по следующей формуле:![]()
![]()
В результате реализации программы получили следующие ответы:
eps1=0.1
x1=2
x2=2
x3=2
n1=5
eps2=0.001
x1=1.5
x2=2
x3=2.5
n2=18
eps3=1e-06
x1=1.5
x2=2
x3=2.5
n3=43
n1, n2, n3 — количество итераций.
Задание 4. Сравнить результаты выполнения задания 3 с результатами решения заданной системы прямыми методами (лабораторная работа 5). Сделать выводы по результатам работы.Решение:
В предыдущей лабораторной работе получила следующие корни, с точностью до десяти цифр:
![]()
![]()
![]()
Сравним результаты, полученные в лабораторной работе 5(часть 1), с результатами задания 3 этой лабораторной работы(2 часть):
ξ=0.1
![]()
![]()
![]()
![]() ξ=0.001
ξ=0.001
![]()
![]()
![]()
ξ=0.000001
![]()
![]()
![]()
Сравнив результаты системы, полученные при решении итерационным методом и прямым методом, можно сказать, что они практически не отличаются. Разница заметна лишь из-за того, что в прямом методе мы не округляли, а в итерационном мы пользуемся функцией округления. Корни отличаются на незначительно малое число.
Похожие работы
о неизвестных в уравнении. А это довольно таки трудоемко, особенно при больших порядках числа n. Еще одним точным методом для решения данных СЛАУ является рассматриваемый в данной работе метод квадратных корней для симметричной матрицы А. Изучать данный метод мы будем следующим образом. Сначала рассмотрим математическую постановку задачи для метода квадратных корней при решении СЛАУ. В данном ...
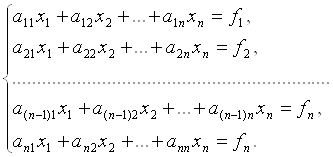
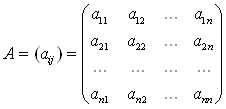
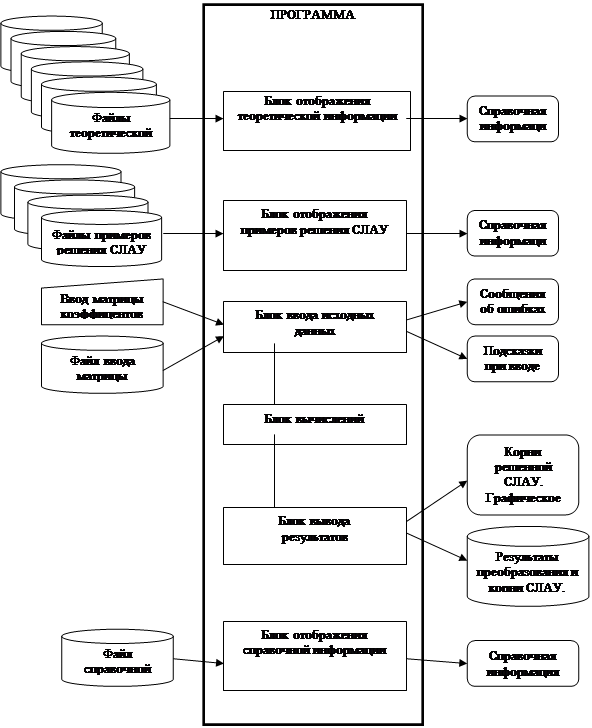
... Рисунок 1.1 - Схема информационных потоков для вычисления СЛАУ методом Гаусса Условные обозначения к рисунку 2.1: - данные, вводимые с клавиатуры - данные, хранящиеся на диске - данные, выводимые на экран 2. Решение систем линейных алгебраических уравнений методом гаусса 2.1 Основные понятия Система линейных алгебраических уравнений (СЛАУ) из m уравнений с n неизвестными ...
... 10.4 9.7 9.7 -8.4 Результат вычислений по методу Гаусса x1 = 5.0000000000E+00 x2 = -4.0000000000E+00 x3 = 3.0000000000E+00 x4 = -2.0000000000E+00 2.2 Программа решения систем линейных уравнений по методу Зейделя 2.2.1. Постановка задачи. Требуется решить систему линейных алгебраических уравнений с вещественными коэффициентами вида a11x1 + a12x2 + … + a1nxn = b1 , a21x2 + ...
... 1.2 0.4 -0.8 -0.8 3.6 4 4.7 10.4 9.7 9.7 -8.4Результат вычислений по методу Гаусса x1 = 5.0000000000E+00 x2 = -4.0000000000E+00 x3 = 3.0000000000E+00 x4 = -2.0000000000E+00 2.2 Программа решения систем линейных уравнений по методу Зейделя 2.2.1. Постановка задачи. Требуется решить систему линейных алгебраических уравнений с вещественными коэффициентами вида a11x1 + a12x2 + … + a1nxn = ...


0 комментариев