Навигация
Автоматизация решения систем линейных алгебраических уравнений
Пояснительная записка: 42 с.,11 рис., 1 табл., 4 источника, 5 прил.
Целью работы над данным курсовым проектом является написание программного продукта для решения систем линейных уравнений. Метод Гаусса. Программный продукт должен выводить на экран теоретическую информацию по теме "Системы линейных алгебраических уравнений. Метод Гаусса", давать возможность решать системы линейных уравнений, а также предоставлять необходимый справочный материал по требованию пользователя.
Результаты работы может быть использованы на производстве, где допускается некоторая погрешность вычислений, а так же школьниками и студентами для сверки решаемых ими задач.
При выполнении данного ПП мною были получены навыки в решении систем линейных уравнений, а также в достаточном объеме изучен язык программирования Pascal 7.0.
РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫЙ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ, МЕТОД ГАУССА.
Содержание
Реферат
Перечень обозначений, символов, единиц, сокращений и терминов
Введение
1. Постановка задачи
1.1 Цель разработки
1.2 Область применения
1.3 Актуальность разработки ПП
1.4 Входные данные
1.5 Выходные данные
1.6 Схема информационных потоков
2. Решение систем линейных алгебраических уравнений методом гаусса
2.1 Основные понятия
2.2 Метод Гаусса. Исключение неизвестных
2.3 Однородная СЛАУ
3. Алгоритм решения задачи
3.1 Водные данные
3.3 Входные данные
3.4 Алгоритм
4. Проектирование интерфейса
5. Описание программной реализации
5.1 Функционально-логическая схема программы
5.2 Описание процедур и функций
5.3 Описание структур и форматов
6. Комплект поставки и порядок установки
7. Тестирование программы
Выводы
Список использованных источников
Приложение А
Приложение Б
Для того, чтобы выйти из программы в окне меню нужно нажать цифру "5". Приложение В
Приложение В
Приложение Г
Приложение Д
Перечень обозначений, символов, единиц, сокращений и терминов
ПП - программный продукт
СЛАУ - система линейных алгебраических уравнений
Введение
В данном курсовом проекте был разработан программный продукт, предназначенный для решения систем линейных алгебраических уравнений методом Гаусса.
![]() Решение систем уравнений, содержит четко сформулированный алгоритм для проведения вычислений.
Решение систем уравнений, содержит четко сформулированный алгоритм для проведения вычислений.
Одним из важнейших разделов математики является раздел, посвященный вычислениям систем линейных уравнений. И это не удивительно, т.к. вычисление систем линейных уравнений присутствует во всех сферах человеческой деятельности.
Весьма существенным преимуществом такого программного продукта является способность предотвращать ошибки человеческого фактора, которые могут возникнуть при вводе информации. Это обусловливается тем, что программа осуществляет проверку на наличие таких ошибок. Если же такие ошибки возникли, то на экран будет выведено предупреждение о неправильном вводе, и пользователю будет предоставлена возможность повторить ввод.
Кроме того, метод в электронном виде достаточно компактен, не имеет больших системных требований, а также рассчитан на широкую аудиторию пользователей.
1. Постановка задачи 1.1 Цель разработки
Целью создания программного продукта является автоматизация процесса решения систем уравнений.
Наличие удобного в использовании графического интерфейса позволяет выбрать одну из предложенных разработчиком функцию для решения систем уравнений и построения графиков. Кроме того, ПП снабжён справочной системой, позволяющей легко получить доступ к интересующей пользователя информации о работе программы, а также теоретическому материалу на тему " Системы линейных алгебраических уравнений методом Гаусса".
1.2 Область примененияИспользование данного ПП возможно в сфере образования в виде вспомогательной программы для школьников и студентов при изучении метода Гаусса, для автоматизации в решении СЛАУ, а также для самоконтроля.
1.3 Актуальность разработки ППЧеловек все чаще прибегает к использованию компьютера для того, чтобы в короткие сроки, и с максимальной эффективностью решать поставленные задачи. Эта программа может выявлять ошибки, к тому же, она в своих расчетах не содержит долю человеческого фактора, что тем самым приводит к более точным расчетам. В работе такие системы способны функционировать без вмешательства человека, осуществлять расчеты самостоятельно, только нуждаясь во вводе информации пользователем.
1.4 Входные данные
Входными данными программы являются введенные с клавиатуры и из файла коэффициенты матрицы, а также вывод информации из файлов. Когда пользователь открывает ПП, на середину экрана выводится меню из текстового файла “menu. txt”. При выборе пункта "Теория" на экран выводится теоретический материал из файлов: “Text1. txt", “Text2. txt”, “Text3. txt", “Text4. txt”, “Text5. txt", “Text6. txt”. При выборе пункта "Пример" на экран выводятся примеры решения СЛАУ методом Гаусса из файлов “Primer1. txt”, “Primer2. txt”, “Primer3. txt”, “Primer4. txt”. При выборе пункта "Справка" на экран выводится справочный материал по программному продукту из файла “SPRAVKA1. txt".
1.5 Выходные данныеВыходными данными являются приведенная к ступенчатому виду матрица, корни СЛАУ и конечный результат, выведенный на экран и записанный в файл “Оtvet. txt".
1.6 Схема информационных потоковВся программа представляет собой одно целое "тело", куда входят пять блоков: блок отображения теоретической информации, блок отображения примеров решения СЛАУ, блок ввода исходных данных, блок вычислений, блок вывода результатов и блок отображения справочной информации. Данные, хранящиеся на диске в блоке отображения теоретической информации, - это файлы теоретической информации, а данные выводимые на экран в этом блоке, - это справочная информация. Данные, хранящиеся на диске в блоке отображения примеров СЛАУ, - это файлы примеров решения СЛАУ, а данные выводимые на экран в этом блоке, - это справочная информация. Данными, вводимыми с клавиатуры в блок ввода исходных данных, являются ввод матрицы коэффициентов, а данные выводимые на экран в этом блоке, - это сообщения об ошибке и подсказки при вводе. В блоке вывода результатов на экран выводятся корни решенной СЛАУ. Графическое решение.
Данные, хранящиеся на диске в блоке отображения справочной информации, - это файлы справочной информации, а данные выводимые на экран, - это справочная информация. На рисунке 2.1 пользователь может проследить все вышеописанное.
Рисунок 1.1 - Схема информационных потоков для вычисления СЛАУ методом Гаусса
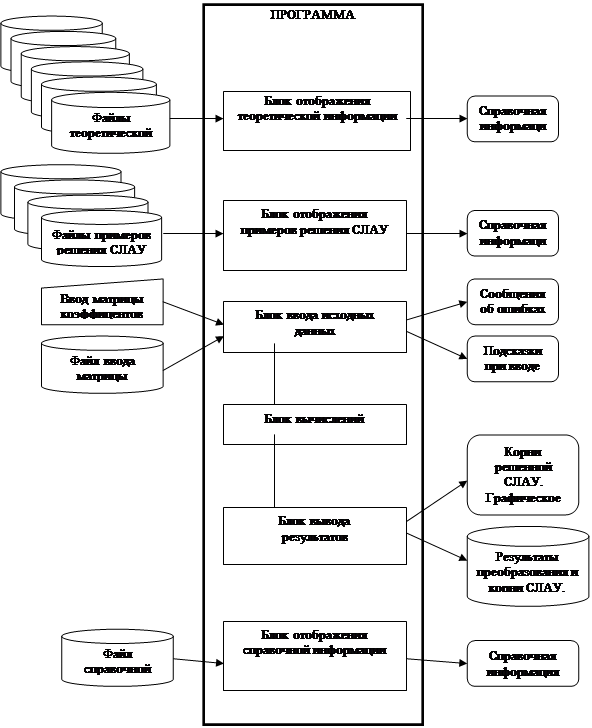 |
Условные обозначения к рисунку 2.1:
 - данные, вводимые с клавиатуры
- данные, вводимые с клавиатуры
 - данные, хранящиеся на диске
- данные, хранящиеся на диске
 - данные, выводимые на экран
- данные, выводимые на экран
2. Решение систем линейных алгебраических уравнений методом гаусса 2.1 Основные понятия
Система линейных алгебраических уравнений (СЛАУ) из m уравнений с n неизвестными х1,..., хn - это система уравнений вида
![]() a11x1+a12x2+... +a1nxn=b1
a11x1+a12x2+... +a1nxn=b1
a21x1+a22x2+... +a2nxn=b2
. ………... ... ... ... ... ... ... ... ..., (2.1)
am1x1+am2x2+... +amnxn=bm
где числа aij (i=1,m; j=1,n) называется коэффициентами СЛАУ, а bi - свободными членами СЛАУ, причем (aij,bi) Є R.
Индекс i обозначает номер уравнения, а индекс j - номер неизвестного.
Система алгебраических уравнений называется линейной, если все уравнения системы содержат неизвестные только первой степени, и они между собой не перемножаются.
СЛАУ называется квадратной, если в ней число уравнений равно числу неизвестных, то есть m=n.
СЛАУ называется однородной, если все ее свободные члены равна нулю, то есть bi=0.
СЛАУ называется неоднородной, если среди ее свободных членов хотя бы один не равен нулю, то есть bi ≠0.
Решение СЛАУ (2.1) называется такая совокупность значений неизвестных x1=C1,...,xn=Cn, которая каждое уравнение СЛАУ обращает в верное числовое равенство (тождество).
СЛАУ называется совместным, если она имеет хотя бы одно решения, и не совместных, если она вообще не имеет решений.
Совместная СЛАУ называется определенной, если она имеет единственное решение, и не определенной, если она имеет более одного решения.
Неопределенная СЛАУ всегда имеет бесконечное множество решений. Тогда каждое ее решение называется частным решением СЛАУ, а множество всех частных решений называется общим решением СЛАУ.
СЛАУ называется эквивалентными, если они имеют одно и тоже множество решений.
Элементарными (тождественными) преобразованиями СЛАУ являются:
1) перестановка уравнений,
2) умножение любого уравнения на число ʎ ≠ 0,3) прибавление одного уравнения к другому.
При элементарных преобразованиях получают только эквивалентные СЛАУ.
2.2 Метод Гаусса. Исключение неизвестныхМетод Гаусса является универсальным, так как применим для исследования на совместность и решение не только квадратных, но и любых СЛАУ. Суть метода: СЛАУ кратко записывают в виде расширенной матрицы, которую с помощью элементарных преобразований над строками приводят к ступенчатому виду.
Этот процесс называют прямым ходом метода Гаусса. В каждой строке ступенчатой матрицы соответствует свое алгебраическое уравнение.
Ступенчатая СЛАУ совместна только тогда, когда она не содержит строк вида <0 0...0 | c>, где с≠0, так как им соответствуют противоречивые равенства вида 0=с. Строки вида <0 0...0 | 0> отбрасываются, так как им соответствует тождество 0≡0.
Решение совместной СЛАУ ступенчатого вида находят так: из последнего уравнения СЛАУ находится значение неизвестной xn и подставляется в вышестоящее уравнение, чтобы найти значение xn-1. Далее, используя значения этих двух неизвестных, поднимаются на ступеньку выше и находят значение xn-2 и так далее. Последним находят значение неизвестной x1 из 1-ого уравнения. Описанный процесс называется обратным ходом метода Гаусса.
2.3 Однородная СЛАУОднородная СЛАУ имеет вид
![]() a11x1+a12x2+... +a1nxn=0
a11x1+a12x2+... +a1nxn=0
a21x1+a22x2+... +a2nxn=0
………... ... ... ... ... ………, (2.2)
am1x1+am2x2+... +amnxn=0
В однородной СДАУ нулевой столбец не меняется при элементарных преобразованиях над строками расширенной матрицы. Поэтому в ней ранг матрицы коэффициентов всегда равен рангу расширенной матрицы. (r (A) =r (Ab)).
Тогда, по теореме Кронекера - Капелли любая однородная СЛАУ всегда совместна и, согласно ее виду, всегда имеет нулевое (тривиальное) решение: x1=... =xn=0. Если при этом ранг матрицы коэффициентов равен числу неизвестных (r (A) =n), то для однородной СЛАУ нулевое решение является единственно возможным.
Теорема 1.
Для того чтобы однородная СЛАУ имела нулевые решения, необходимо и достаточно, чтобы ранг матрицы коэффициентов был меньше числа неизвестных (r (A) <n).
Доказательство.
1) Необходимость. Предположим обратное, то есть, что r (A) =n, где n - число неизвестных. Тогда порядок базисного минора Mn будет равен n, так как r (Mn) =r (A) =n. Следовательно, по формулам Крамера однородная СЛАУ будет иметь единственное решение - нулевое: xi = Δi / Δ = 0, где Δi = 0,a Δ ≠ 0. Таким образом, при r (A) =n однородная СЛАУ ненулевых решений не имеет.
2) Достаточность. Пусть r (A) <n, тогда по следствию 2 теоремы Кронекера-Копелли однородная СЛАУ будет совместной и неопределенной, то есть она будет иметь бесконечное множество решений, в том числе и нулевых. Fin.
Теорема 2.
Для того чтобы квадратная однородная СЛАУ имела нулевые решения, необходимо и достаточно, чтобы ее главный определитель был равен нулю (Δ=0). Доказательство.
1) Необходимость. По вышеприведенной теореме 1, если однородная СЛАУ имеет нулевые решения, то ранг ее матрицы коэффициентов должен быть меньше числа неизвестных (r (A) <n). Следовательно, главный определитель квадратной однородной СЛАУ должен быть равен нулю (Δ=0).
2) Достаточность. Если главный определитель квадратной однородной СЛАУ равен нулю (Δ=0), то ранг ее матрицы коэффициентов будет меньше числа неизвестных (r (A) <n). Поэтому такая СЛАУ имеет бесконечное множество ненулевых решений. Fin.
Теорема 2.
Для того чтобы квадратная однородная СЛАУ имела нулевые решения, необходимо и достаточно, чтобы ее главный определитель был равен нулю (Δ=0). Доказательство.
1) Необходимость. По вышеприведенной теореме 1, если однородная СЛАУ имеет нулевые решения, то ранг ее матрицы коэффициентов должен быть меньше числа неизвестных (r (A) <n). Следовательно, главный определитель квадратной однородной СЛАУ должен быть равен нулю (Δ=0).
2) Достаточность. Если главный определитель квадратной однородной СЛАУ равен нулю (Δ=0), то ранг ее матрицы коэффициентов будет меньше числа неизвестных (r (A) <n). Поэтому такая СЛАУ имеет бесконечное множество ненулевых решений.
3. Алгоритм решения задачи 3.1 Водные данные
Входными данными в алгоритме решения систем линейных уравнений методом Гаусса являются:
А: массив [1…N, 1…N] вещ. {матрица}
В: массив [1…N] вещ. {массив свободных коэффициентов}
N: цел. {размер матрицы}
3.2 Промежуточные данныеПромежуточные данные в алгоритме решения систем линейных уравнений методом Гаусса являются:
l: цел. {Индекс элементов. Номер строки,
которую обрабатываем}
i: цел {номер "Базовой строки"}
К: вещ. {множитель для l - ой строки}
kol: цел {количество нулей в текущей строке}
S: вещ. {сумма элементов, вычисляемая
при обратном ходе метода Гаусса}
3.3 Входные данныеВыходные данные в алгоритме решения систем линейных уравнений методом Гаусса являются:
х: массив [1…N] вещ. {массив ответов}
Rez: цел. {количество решений матрицы:
0 - ни одного; 1 - одно; 2 - ∞}
3.4 Алгоритм
На рисунке 3.1 изображен ввод размера матрицы, который должен быть больше нуля
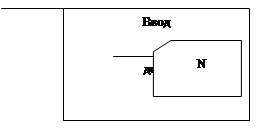
Рисунок 3.1 Ввод
На рисунке 3.2 изображен цикл ввода коэффициентов.
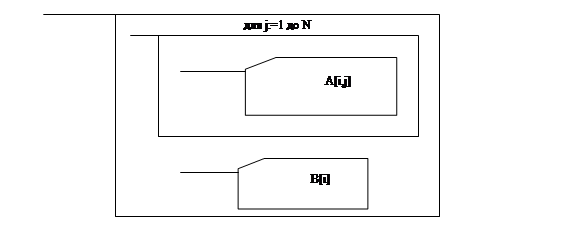 |
для i: =1 до N
Рисунок 3.2 Цикл.
На рисунке 3.3 изображен цикл приведения матрицы к ступенчатому виду и нахождение корней.
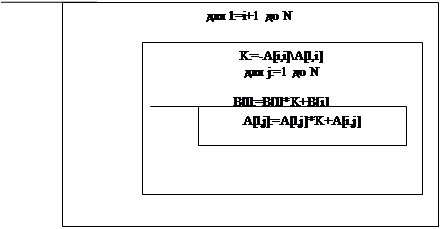 |
для i: =1 до N-1
Рисунок 3.3 Ступенчатый вид
На рисунке 3.4 показано что происходит если переменной Rez присваиваются значения 0, 1,2.
Rez: =1
для i: =1 до N
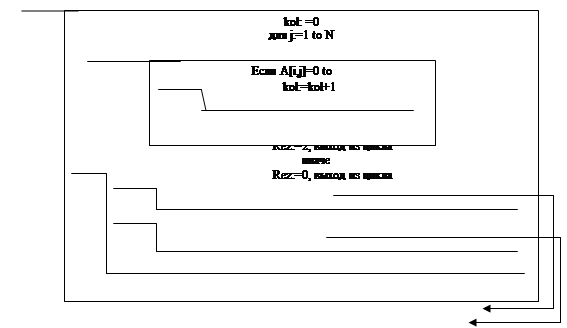
Рисунок 3.4 Переменная Rez
Рисунок 3.5 является продолжением рисунка 3.4
если Rez=1 to
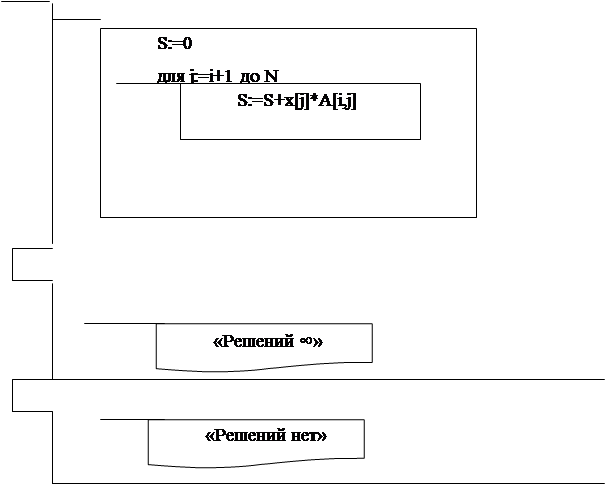 для i:=N-1 до 1 шаг -1
для i:=N-1 до 1 шаг -1
{Вывод матрицы А и вектора х}
Иначе
Если Rez = 0 то
Вывод
Иначе вывод
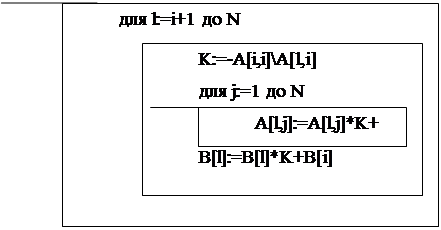 Рисунок 3.5 Переменная Rez.
Рисунок 3.5 Переменная Rez.
4. Проектирование интерфейса
В данном программном продукте был использован текстовый интерфейс, т.к. разработчик отдает ему большее предпочтение. Был выбран комбинированный режим. Текстовый - для написания интерфейса, графический - для рисования графиков.
Меню интерфейса состоит из 5 пунктов каждому из которых соответствует своя цифра:
пункт вида "1 - Теория", означает, что для вызова теоретической информации нужно нажать клавишу 1;
пункт вида "2 - Пример", означает, что для вызова примера решения СЛАУ методом Гаусса нужно нажать клавишу 2;
пункт вида "3 - Решение", означает, что для вызова диалогового окна, где будет предложено пользователю ввести свои коэффициенты для решении СЛАУ, нужно нажать клавишу 3;
пункт вида "4 - Справка", означает, что для вызова справочной информации нужно нажать клавишу 4;
пункт вида "5 - Выход", означает, что для выхода из программы нужно нажать клавишу 1;
Статусная строка отображает информацию следующего вида:
подсказки пользователю, относительно дальнейших действий: " Нажмите номер пункта меню", "Для перехода укажите номер страницы (от 1 до 6), "Для возврата в меню нажмите Esc, для вывода справки нажмите 0", "Для возврата назад нажмите 1".
5. Описание программной реализации 5.1 Функционально-логическая схема программы
Данная схема отражает укрупненный алгоритм работы программы с учетом интерфейсных решений (см. рисунок 5.1).
Вначале происходит прорисовка главного окна программы, в результате чего на экран выводятся 5 пунктов главного меню. Если выбрана первый пункт (1 - Теория), то происходит вывод теоретической информации на экран. Если выбрана второй пункт меню (2 - Пример) - вывод примера решения СЛАУ на экран. Если выбрана третий пункт (3 - Решение) - происходит решение СЛАУ методом Гаусса. Если выбран четвертый пункт (4 - Справка) - на экран выводится справочная информация по методу Гаусса. Если выбран пятый пункт (5 - Выход) - происходит полный выход из программы. Если не выбран ни один пункт меню, на экране ничего не происходит.
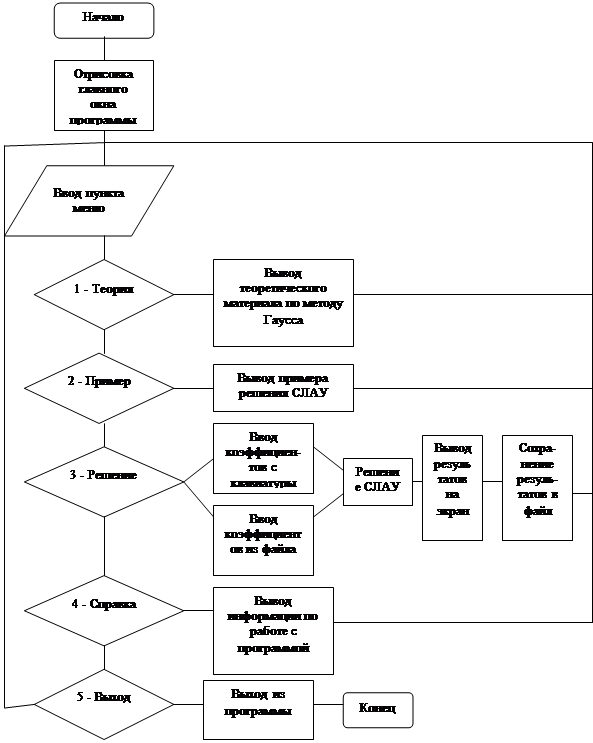 |
Рис.5.1 Функционально - логическая схема программы 5.2 Описание процедур и функций
Процедура LoadFile (Name: string); - открывает текстовые файлы.
Name - имя открываемого файла.
Процедура menu; - выводит на экран главное меню.
Процедура menuTeorii; - выводит на экран файл с меню для теории.
Процедура menuSpravki; - выводит на экран файл с меню для справки.
Процедура menuPrimera; - выводит на экран файл с меню для примера.
Процедура Spravka (var n: char); - выводит на экран справочную информацию.
n - номер открываемой страницы.
Процедура Teoria ( var n: char); - выводит на экран теоретическую информацию.
n - номер открываемой страницы.
Процедура Grafik (а1, b1, c1, a2, b2, c2, xc, yc: real); - выводит на экран график.
а1, b1, c1, a2, b2, c2, xc, yc - коэффициенты матрицы.
Процедура Vvod (var x: real; var code: integer); - процедура для ввода вещественного числа.
x - вещественное число,
соde - переменная ошибки.
Процедура Vvod1 (var n: integer); - процедура для ввода целого числа.
n - целое число;
Процедура Rewenie; - решение СЛАУ.
Процедура Primer - выводит на экран примеры решения СЛАУ методом Гаусса.
Процедура Vuxod - выводит пользователя из программы.
5.3 Описание структур и форматовВ исходном текстовом файле хранится информация в следующем формате (разделитель между элементами матрицы - один или несколько пробелов):
(размер матрицы)
(элементы матрицы).
Пример исходного файла:
4
1 5 2 3 5
1 5 6 9 4
1 4 5 6 4
3 6 5 4 8
6. Комплект поставки и порядок установки
В комплект поставки входят следующие файлы:
EGAVGA. BGI - файл драйвера графического режима;
GRAPH. TRU-модуль графического режима;
“menu. txt" - главное меню интерфейса;
“Text1. txt", “Text2. txt”, “Text3. txt", “Text4. txt”, “Text5. txt", “Text6. txt" - теоретический материал.
“Primer1. txt”, “Primer2. txt”, “Primer3. txt”, “Primer4. txt" - примеры решения СЛАУ.
“SPRAVKA1. txt" - справочный материал.
OSNOVN2 - весь программный продукт.
Чтобы установить программу на ПК, необходимо просто скопировать папку с программой, в которой содержатся все вышеупомянутые файлы, на диск, с которого пользователь хочет вести работу. Чтобы начать работу с программой, необходимо запустить файл OSNOVN2.
7. Тестирование программы
Для тестирования программы разработчик решил несколько СЛАУ вручную, а потом ввел в программу такие же коэффициенты как и для ручного просчета. Вот что получилось:
1) Исходная матрица:
1 1 1
2 2 1
Преобразованная матрица:
1 1 1
0 0 - 1
Решений нет. Ответ программы совпадает с ручным просчетом.
2) Исходная матрица:
1 1 2
1 - 1 0
Преобразованная матрица:
1 1 2
0 2 2
Вектор ответов:
х [1] = 1
х [2] = 1
Ответ программы совпадает с ручным просчетом.
Выводы
В процессе написания курсового проекта был создан пакет прикладных программ для реализации алгоритма решения систем линейных уравнений с помощью ПК.
Достоинства данного метода, а также программы состоят в том, что с их помощью можно решать систем линейных уравнений, а также вычислять неизвестные переменные, не затрачивая времени на вычисления.
Недостатком данного ПП является то, что программа может иметь мелкие погрешности.
Если же говорить об интерфейсе программы, то следует отметить его простоту и легкость использования, поэтому с программой способен работать даже человек, который впервые имеет дело с компьютерами.
Автор надеется, что после доработки программы, ПП можно будет использовать на производстве.
Также следует отметить, что во время написания курсового проекта, автор изучил основы языка Turbo Pascal 7.0.
Список использованных источников
1. Турбо Паскаль 7.0/ Алексеев Е.Р., Чесноков О.В. - М.: НТ Пресс, 2004. - 320с
2. Марченко А.И., Марченко Л.А. Программирование в среде Тurbo Рascal 7.0. - 6-е изд. стереотип. _Юбилейное - К.: ВЕК++, 2000 - 127с. э
3. Петренко И.В., Беда Е.Н. Лекции и практикум по линейной алгебре: Учебное э пособие. - Донецк: ИПИИ "Наука 1 освіта"; 2005. - 76с.
4. Культин Н.Б. Программирование в Turbo Pasсal 7.0 и Delphi / Второе издание, переработанное и дополненное. - СПб.: БХВ - Санкт Петербург, 1999. - 416 с., ил.
Приложение А
ТЕХНИЧЕСКОЕ ЗАДАНИЕ
А.1. Общие сведения
Основанием для разработки курсовой работы "Метод Гаусса" являетсязадание, выданное кафедрой Программного обеспечения интеллектуальных систем (ПОИС).
Плановый срок начала работы: 15 февраля 2007 г.
Дата защиты работы: 29 мая 2007 г. ж
Курсовая работа выполняется согласно графику, приведенному в таблице А.1.
Таблица А.1. - График выполнения курсовой работы
| № | Этапы работы | Срок выполнения |
| 1 | Постановка задачи: определение требований к программному комплексу. | 15.02-22.02 |
| 2 | Составление технического задания. | 22.02-01.03 |
| 3 | Разработка методов решения задачи. | 01.03-08.03 |
| 4 | Разработка алгоритма функционирования программы. | 15.03 |
| 5 | Определение структур входных и выходных данных, алгоритмов работы модулей. Описание входных и выходных данных. | 22.03 - 29.03 |
| 6 | Написание программы. | 05.04-19.04 |
| 7 | Отладка программы. | 19.04-26.04 |
| 8 | Тестирование программы. | 26.04-03.05 |
| 9 | Написание пояснительной записки. | 03.05-17.05 |
| 10 | Защита курсовой работы | 29.05 |
А.2. Назначение и цели создания программы
Курсовая работа предназначена для помощи в обучении решения систем алгебраических уравнений методом Гаусса. Проект может быть использован в общеобразовательных школах учениками старших классов, а также студентами математических специальностей высших учебных заведений.
А.З. Требования к программному продукту
А.3.1 Требования к программному продукту в целом;
В целом к ПП предоставляются такие требования:
интуитивно - понятый интерфейс
наличие меню;
наличие контекстных подсказок для текущих и возможных действий пользователя
вывод подсказок при вводе данных;
предоставление справочной информации по методу Гаусса, причем исходная информация должна храниться во внешних файлах.
решение задач в рамках метода Гаусса. Предоставление пользователю возможности получить решение для конкретных входных данных с выводом результатов на экран и сохранением в файл.
использование графических средств при решении задач или предоставлении теоретического материала по методу Гаусса.
А.3.2 Требования к задачам и функциям, выполняемым программой;
исходная матрица должна вводиться как с клавиатуры, так и из текстового файла;
для СЛАУ второго ранга должно выводиться графическое решение.
пользователю должна быть предоставлена справочная информация по методу Гаусса;
результаты вычисления должны выводиться на экран и сохраняться в текстовый файл;
А.3.3 Требование к программному обеспечению Требованиями ПО:
ОС МS Windows XP Professional;
наличие Турбо Паскаль.
А.3.4 Требования к техническому обеспечению
Для нормального функционирования программного продукта на машине требуется:
процессор АВМ Аt1оn;
операционная память (не менее 64 кб);
клавиатура;
свободное дисковое пространство (не менее 128 мб);
А.3.5 Требование к организационному обеспечению Требования к ОО:
пояснительная записка;
приложения:
техническое задание;
руководство пользователя;
экранные формы;
тексты программ;
результаты работы.
Приложение Б
РУКОВОДСТВО ПОЛЬЗОВАТЕЛЯ
Данный программный продукт предназначен для помощи в обучении систем алгебраических уравнений методом Гауcса. Программа может быть использована в общеобразовательных школах учениками старших классов, а также студентами математических специальностей высших учебных заведений.
Для того, чтобы войти в пункт "Теория" в окне меню нужно нажать цифру "1". Этот пункт служит для того, чтоб пользователь смог ознакомиться с теоретической стороной решения СЛАУ. Теория состоит из шести страниц, каждую из которых можно вывести на экран путем нажатием соответствующей страницы от 1 до 6. Для вывода на экран справки из пункта "Теория" нажмите цифру "0". Для возврата в главное меню нажмите "ESC".
Для того чтобы войти в пункт "Пример" в окне меню нужно нажать цифру "2". Этот пункт состоит из трех страниц, каждую из которых можно вывести на экран путем нажатия соответствующей цифры от 1 до 3. Для вызова справки нажмите цифру "7". Для выхода в главное меню нажмите "Esc".
Для того, чтобы войти в пункт "Решение" в окне меню нужно нажать цифру "3". Далее следуйте подсказкам внизу экрана. Для вызова справки нажмите цифру "0". Для выхода в главное меню нажмите "Esc".
Для того, чтобы войти в пункт "Справка" в окне меню нужно нажать цифру "4". Для выхода в главное меню нажмите "Esc".
Для того, чтобы выйти из программы в окне меню нужно нажать цифру "5".Приложение В
ЭКРАННЫЕ ФОРМЫ
На рисунок В.1 отображено главное меню текстового интерфейса.
На рисунке В.2 отображено окно теории.
На рисунке В.3 отображено окно справочной информации.
На рисунке В.4 отображено окно примера решения СЛАУ.
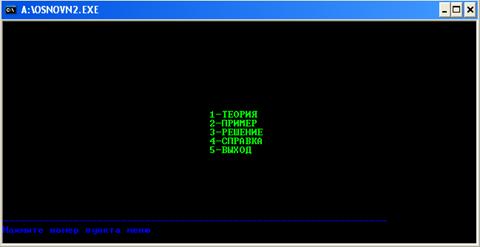
Рисунок В.1 Главное меню
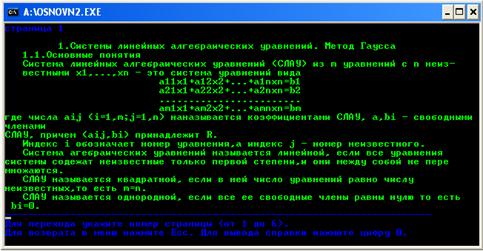
Рисунок В.2 Теория
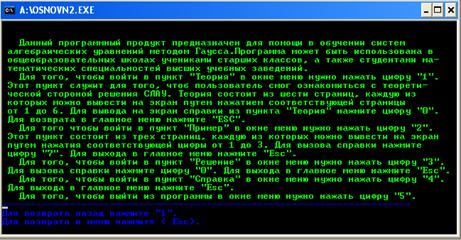
Рисунок В.3 Справка
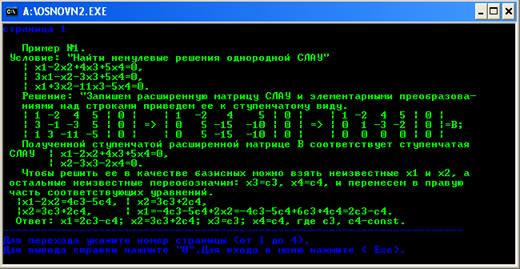
Рисунок В.4 Пример
Приложение Г
РЕЗУЛЬТАТЫ РАБОТЫ ПРОГРАММЫ
На рисунке Г.5 отображено окно решения матрицы на первом шаге. На рисунке Г.6 отображено окно решения матрицы на втором шаге и преобразованная матрица, а также вектор ответов.
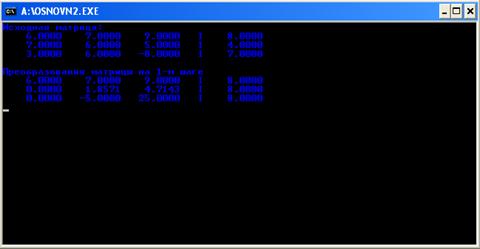
Рисунок Г.5 Решение на первом шаге
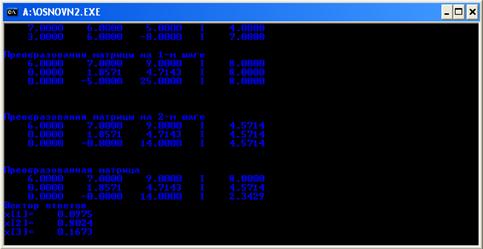
Рисунок Г.6 Ответы
Приложение Д
ЛИСТИНГ ПРОГРАММЫ
uses Crt, graph;
Var ch: char;
const Nmax=100;
Procedure LoadFile (Name: string);
Var f: text; S: string; code: integer;
Begin
assign (f,Name);
{$I-}
reset (f);
code: =Ioresult;
if code<>0 then
writeln ('Ошибка. Файл не найден! ')
else begin {clrscr}
gotoxy (1,3);
textcolor (10);
TextBackground (0);
while not eof (f) do
begin
readln (f,S);
writeln (S);
end;
close (f);
end;
End;
Procedure menu;
Begin
TextBackground (0);
clrscr;
LoadFile ('A: MENU. txt');
textcolor (9);
TextBackground (0);
gotoxy (1,23);
writeln ('-----------------------------------------------------------------');
gotoxy (1,24);
writeln ('Нажмите номер пункта меню');
end;
procedure menuTeorii;
begin
clrscr;
textcolor (9);
TextBackground (0);
gotoxy (1,23);
writeln ('------------------------------------------------------------------------');
gotoxy (1,24);
writeln ('Для перехода укажите номер страницы (от 1 до 6). ');
writeln ('Для возврата в меню нажмите Esc. Для вывода справки нажмите цифру 0. ');
end;
procedure menuSpravki;
begin
clrscr;
textcolor (9);
TextBackground (0);
gotoxy (1,23);
writeln ('------------------------------------------------------------------------');
gotoxy (1,24);
writeln ('Для возврата назад нажмите "1". ');
writeln ('Для возврата в меню нажмите (Esc). ');
end;
procedure menuPrimera;
begin
clrscr;
textcolor (9);
TextBackground (0);
gotoxy (1,23);
writeln ('------------------------------------------------------------------------');
gotoxy (1,24);
writeln ('Для перехода укажите номер страницы (от 1 до 4). ');
writeln ('Для вывода справки нажмите "0". Для входа в меню нажмите (Esc). ');
end;
procedure Spravka;
var n: char; {номер страницы}
begin
menuSpravki;
gotoxy (1,1);
LoadFile ('A: Spravka1. txt');
repeat
n: =readkey; until n in ['1',#27] ;
case n of
'1': begin
end;
end;
end;
procedure Teoria;
var n: char; {номер страницы}
begin
menuTeorii;
gotoxy (1,1);
writeln ('страница 1');
LoadFile ('A: Text1. txt');
repeat
repeat n: =readkey; until n in ['0'. '6',#27] ;
case n of
'1': begin
menuTeorii;
gotoxy (1,1);
writeln ('страница 1');
LoadFile ('A: Text1. txt');
end;
'2': begin
menuTeorii;
gotoxy (1,1);
writeln ('страница 2');
LoadFile ('A: Text2. txt');
end;
'3': begin
menuTeorii;
gotoxy (1,1);
writeln ('страница 3');
LoadFile ('A: Text3. txt');
end;
'4': begin
menuTeorii;
gotoxy (1,1);
writeln ('страница 4');
LoadFile ('A: Text4. txt');
end;
'5': begin
menuTeorii;
gotoxy (1,1);
writeln ('страница 5');
LoadFile ('A: Text5. txt');
end;
'6': begin
menuTeorii;
gotoxy (1,1);
writeln ('страница 6');
LoadFile ('A: Text6. txt');
end;
'0': begin
Spravka;
gotoxy (1,1);
LoadFile ('A: Spravka1. txt');
end;
end;
until n=#27;
end;
procedure grafic (a1,b1,c1,a2,b2,c2,xc,yc: real);
var
minx,maxx,miny,maxy: real;
mx,my: real;
x1,y1,x2,y2: integer;
x0,y0: integer;
grDriver: Integer;
grMode: Integer;
ErrCode: Integer;
begin
grDriver: = Detect;
InitGraph (grDriver, grMode,'c: \bps\bin\egavga. bgi');
ErrCode: = GraphResult;
if ErrCode = grOk then
begin
minx: =xc-2*xc;
maxx: =xc+2*xc;
miny: =yc-2*yc;
maxy: =yc+2*yc;
mx: =getmaxx;
mx: =mx/ (maxx-minx);
my: =getmaxy/ (maxy-miny);
y0: =round (abs (xc) *mx);
x0: =round (abs (yc) *my);
setcolor (white);
line (x0,0,x0,getmaxy);
line (0,y0,getmaxx,y0);
setcolor (red);
x1: =x0+round (minx*mx);
y1: =y0-round ( (c1-a1*minx) /b1*my);
x2: =x0+round (maxx*mx);
y2: =y0-round ( (c1-a1*maxx) /b1*my);
line (x1,y1,x2,y2);
setcolor (yellow);
x1: =x0+round (minx*mx);
y1: =y0-round ( (c2-a2*minx) /b2*my);
x2: =x0+round (maxx*mx);
y2: =y0-round ( (c2-a2*maxx) /b2*my);
line (x1,y1,x2,y2);
Readkey;
CloseGraph;
end
else
Writeln ('Ошибка работы с графикой: ', GraphErrorMsg (ErrCode));
end;
{$S-}
procedure vvod (var x: real; var code: integer);
var s: string;
begin
readln (s);
val (s,x,code);
if code<>0 then
writeln ('Ошибка, повторите ввод');
end;
procedure vvod1 (var n: integer);
var s: string;
code: integer;
begin
repeat
write ('Введите количество элементов матрицы');
readln (s);
val (s,n,code);
if (code<>0) or (N<0) or (N>Nmax) then
writeln ('Ввод не верный. Повторите ввод... ');
until (N>0) and (N<=Nmax) and (code=0);
end;
procedure Rewenie;
var
x: array [1. Nmax] of real;
A: array [1. Nmax,
Похожие работы
... , действующий из нормированного пространства Z в нормированное пространство U. В 1963 г. А.Н.Тихонов дал знаменитое определение регуляризирующего алгоритма (РА), которое лежит в основе современной теории некорректно поставленных задач. Определение. Регуляризирующим алгоритмом (регуляризирующим оператором) называется оператор, обладающий двумя следующими свойствами: 1) определен для любых δ ...
... свести к вычислению четырех определителей третьего порядка. 3-ий учебный вопрос ТЕОРЕМА КРАМЕРА Применим рассмотренную теорию определителей к решению систем линейных уравнений. 1. Система двух линейных уравнений с двумя неизвестными. (3) Здесь х1, х2 – неизвестные; а11, …, а22 – коэффициенты при неизвестных, занумерованные двумя индексами, где первый ...
... уравнений (2) сводится к последовательному решению двух следующих систем уравнений с треугольными матрицами коэффициентов L Y = B; (6) U X = Y (7) линейный алгебраический уравнение численный где Y = - вектор вспомогательных переменных. Такой подход позволяет многократно решать системы линейных ...
... - анализатор Web. Эти программы позволяют получить статистические оценки функционирования выбранной конфигурации. Глава 2. Описание модуля электронного учебника по теме "Методы организации сложных экспертиз компьютерных систем" 2.1 ПОНЯТИЕ И ТРЕБОВАНИЯ К ЭЛЕКТРОННОМУ УЧЕБНИКУ Большие трудности часто возникают при оперативной подготовке, изготовлении и распространении учебных пособий ...


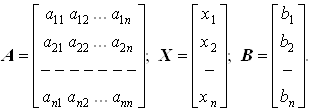





0 комментариев