Навигация
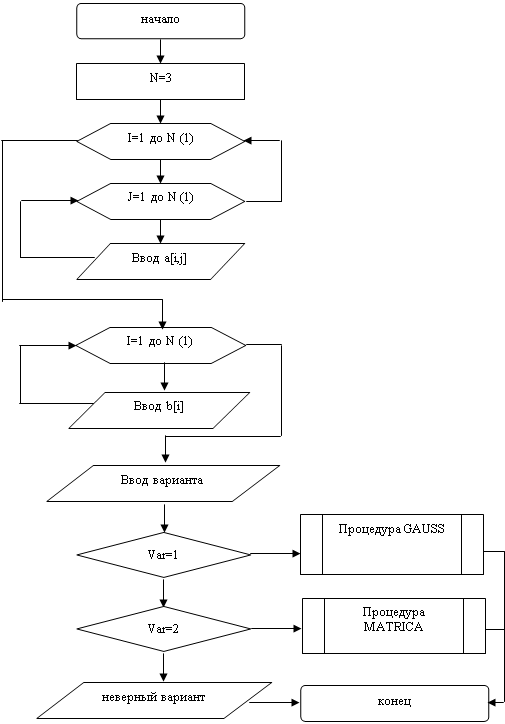
3. Анализ результатов.
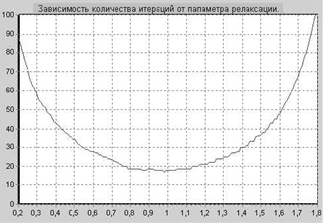
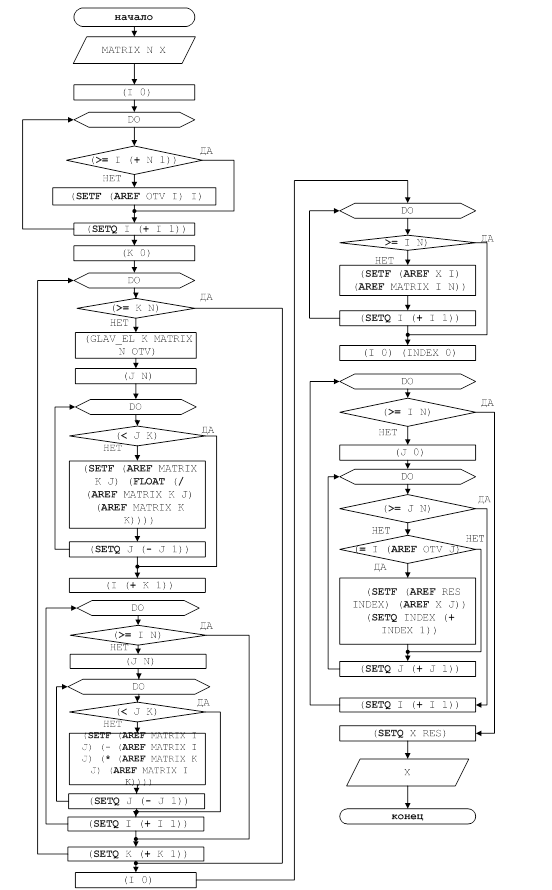
Скорость сходимости итерационного процесса зависит от заданной матрицы коэффициентов. В зависимости от вида исходных данных( матрицы коэффициентов и матрицы b) программа подбирает оптимальный параметр релаксации w(при котором решение достигается за минимальное число итераций). Для достижения наивысшей скорости сходимости итерационного процесса для уравнения, заданного на рис.3 программой был выбран параметр релаксации w=1,26. Таким образом, была применена верхняя релаксация. Заданная точность e=0,0001 была достигнута за 40 итераций. График зависимости количества итераций от параметра релаксации приведен на рис 1.
 |
Рис. 1 Для достижения наивысшей скорости сходимости итерационного процесса для уравнения, заданного на рис.4 программой был выбран параметр релаксации w=0,98. Таким образом, была применена нижняя релаксация. Заданная точность e=0,0001 была достигнута за 17 итераций. График зависимости количества итераций от параметра релаксации приведен на рис 2.
Вывод
Программа, разработанная в данной курсовой работе, реализует метод Зейделя для решения СЛАУ 6-го порядка. Она даёт гарантированно правильное решение системы линейных уравнений, если каждый элемент главной диагонали матрицы коэффициентов является единственным максимальным в своей строке, ненулевым, либо справедливы условия: максимальный элемент строки является единственным максимальным в своём столбце, ненулевым, а ни один из остальных элементов столбца не является максимальным в своей строке, все элементы каждой строки кроме максимального одинаковы.
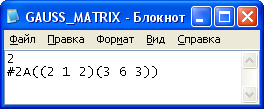
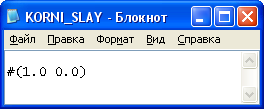
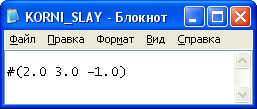
При исходных данных:
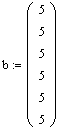

была достигнута точность 0,0001 в решении:
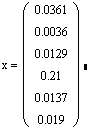 |
за 2 итерации при параметре релаксации w=0,97.
Программа строит график зависимости количества итераций от параметра релаксации для данной СЛАУ, находит параметр релаксации w, при котором решение достигается за минимальное количество итераций и, разумеется, само решение. Программа проста в эксплуатации и нетребовательна к ресурсам. Реализованная в современной среде разработки Delphi 5.0, она без труда может быть доработана или исправлена.
Недостатки программы: 1) применима не для всех систем линейных уравнений; 2)оптимальный параметр релаксации w вычисляется методом подбора, и, поэтому, количество итераций, требуемое для его отыскания достаточно велико(около 18000), однако, для современных ПК, это не является затруднением.
Список использованной литературы
1. Волков Е.А. Численные методы. ¾ М.: Наука, 1987. ¾ 254 с.
2. Калиткин Н.Н. Численные методы. ¾ М.: Наука, 1978. ¾ 512 с.
3. Мудров А.Е. Численные методы для ПЭВМ на языках БЕЙСИК, ФОРТРАН и ПАСКАЛЬ. ¾ Томск, МП "Раско", 1992. ¾270 с.
4. Самарский А.А., Гулин А.В. Численные методы. ¾ М.: Наука, 1989. ¾432с.
5. Кэнту М. Delphi 4 для профессионалов ¾ СПб: «Питер», 1999 ¾1200с.
6. Delphi 5.0 help.
Приложение(распечатка программы, результатов)
Распечатка программы:
unit kurs1;
interface
uses
Windows, Messages, SysUtils, Classes, Graphics, Controls, Forms, Dialogs,
Grids, StdCtrls, ComCtrls, ToolWin, Menus, Unit1, TeEngine, Series,
ExtCtrls, TeeProcs, Chart;
type
TFormk1 = class(TForm)
StringGrid1: TStringGrid;
Label2: TLabel;
Label3: TLabel;
Label4: TLabel;
StringGrid2: TStringGrid;
Label5: TLabel;
Label6: TLabel;
StringGrid3: TStringGrid;
Label7: TLabel;
Label8: TLabel;
Button1: TButton;
MainMenu1: TMainMenu;
Chart1: TChart;
N2: TMenuItem;
N3: TMenuItem;
N4: TMenuItem;
N1: TMenuItem;
Label1: TLabel;
Series1: TFastLineSeries;
procedure FormCreate(Sender: TObject);
procedure matrix;
procedure Button1Click(Sender: TObject);
procedure N1Click(Sender: TObject);
procedure N3Click(Sender: TObject);
procedure N4Click(Sender: TObject);
procedure decision;
private
{ Private declarations }
public
{ Public declarations }
end;
var
Formk1: TFormk1;
// formk1: Tmainmenu;
implementation
var
n,m,i,j,k,l,number_of_iteration,min :integer;
delta,E,sum,max,W,tmp :extended;
A : array[1..6,1..6] of extended;
B : array[1..6] of extended;
X : array[1..6] of extended;
Xp: array[1..6] of extended;
am: array[1..200] of integer;
W_all:array[1..200] of extended;
procedure TFormk1.matrix;
begin
randomize;
for i:=1 to n do stringgrid1.cells[i-1,0]:='*X'+inttostr(i);
for i:=0 to n-1 do
for j:=1 to m do
StringGrid1.cells[i,j]:='2';
for i:=0 to n-1 do
StringGrid1.cells[i,i+1]:='3';
end;
{$R *.DFM}
procedure Tformk1.decision;
begin
delta:=E+1;
number_of_iteration:=0;
for i:=1 to 6 do X[i]:=B[i]/A[i,i];
while (delta>E) and (number_of_iteration < 100) do
begin
for i:=1 to 6 do Xp[i]:=X[i];
for i:=1 to 6 do
begin
sum:=0;
for j:=1 to 6 do sum:=sum+A[j,i]*X[j];
X[i]:=W*(B[i]- sum + A[i,i]*X[i])/A[i,i] + (1-W)*Xp[i];
end;
delta:=abs(X[1]-Xp[1]);
for i:=1 to 6 do
if abs(X[i]-Xp[i])>delta then delta:=abs(X[i]-Xp[i]);
inc(number_of_iteration);
end;
end;
procedure TFormk1.FormCreate(Sender: TObject);
begin
n:=6;m:=6;
matrix;
randomize;
stringgrid2.cells[0,0]:='*1';
for j:=1 to m do
StringGrid2.cells[0,j]:='5';
end;
procedure TFormk1.Button1Click(Sender: TObject);
begin
series1.clear;
for i:=0 to n-1 do
for j:=1 to m do
A[i+1,j]:=strtofloat(StringGrid1.cells[i,j]);
for j:=1 to m do
B[j] :=strtofloat(StringGrid2.cells[0,j]);
for i:=1 to 6 do
begin
max:=abs(A[1,i]);
for j:=1 to 6 do
if abs(A[j,i])>=abs(max) then
begin
max:=A[j,i];
m:=j;
end;
if m<>i then
begin
for l:=1 to 6 do
begin
tmp:=A[l,m];
A[l,m]:=A[l,i];
A[l,i]:=tmp;
end;
tmp:=b[m];
b[m]:=b[i];
b[i]:=tmp;
end;
end;
E:=0.0001;
W:=0.2;
l:=0;
while W<=1.8 do
begin
decision;
inc(l);
am[l]:=number_of_iteration;
W_all[l]:=W;
series1.addxy(W,number_of_iteration,'',clteecolor);
W:=W+0.01;
end;
min:=am[1];
for i:=1 to 200 do
if (am[i]<=min) and (am[i]<>0) then
begin
min:=am[i];
W:=W_all[i];
end;
decision;
if (number_of_iteration>100) or (delta>E) then
begin
label2.Caption:='Программа не может решить данную СЛАУ.';
label3.Visible:=false;
end
else
begin
Chart1.BottomAxis.Automatic:=false;
Chart1.BottomAxis.minimum:=0.2;
Chart1.BottomAxis.maximum:=1.8;
Chart1.BottomAxis.increment:=0.1;
Chart1.LeftAxis.Automatic:=false;
Chart1.LeftAxis.minimum:=0;
Chart1.LeftAxis.maximum:=100;
Chart1.LeftAxis.increment:=5;
label6.visible:=false;
label7.visible:=true;
label8.visible:=true;
label1.visible:=true;
StringGrid3.visible:=true;
stringgrid3.cells[0,0]:='*1';
for i:=1 to 6 do
StringGrid3.cells[0,i]:=floattostr(X[i]);
end;
end;
procedure TFormk1.N1Click(Sender: TObject);
begin
close;
end;
procedure TFormk1.N3Click(Sender: TObject);
begin
chart1.visible:=true;
end;
procedure TFormk1.N4Click(Sender: TObject);
begin
chart1.Visible:=false;
end;
end.
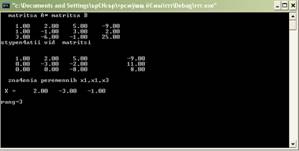
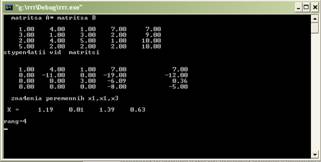
Результаты, рис. 3 и 4:
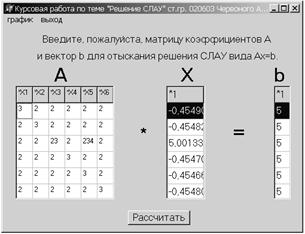
Рис. 3
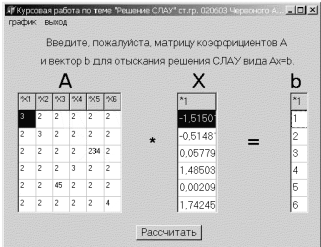 |
Рис. 4
Похожие работы
... строке матрицы i2-ю, умноженную на число r; процедура MultMatr предназначена для умножения матриц. Функция Sign используется для изменения знака на противоположный при вычислении обратной матрицы. Программа настроена на решение системы 3-х линейных уравнений с тремя неизвестными. Чтобы решить систему из 2-х уравнений с 2-мя неизвестными необходимо в программе изменить значение константы N с ...
... 4.Исходный текст программы Составить программу решения систем линейных алгебраических уравнений с квадратной невырожденной матрицей порядка n методом Гаусса с использованием языка С++ . // Решение системы линейных уравнений методом Гаусса. #include<io.h> #include "stdio.h" #include "conio.h" #include <windows.h> #include <iostream> #include <time.h> #include ...
... треугольной матрицей. Вычисления значений неизвестных производят на этапе обратного хода. Целью данной курсовой работы является численное решение системы линейных уравнений с помощью метода исключения Гаусса с выбором главного элемента по столбцу. 1 Постановка задачи Задача ставится следующим образом. Пусть требуется найти решение системы линейных алгебраических уравнений a1,1x1 + a1, ...
... , ary2s Типы данных для переменных, в которых хранятся значения коэффициентов системы Unit2 Gauss1 Процедура для решения системы линейных уравнений методом Гаусса Unit2 Gaussj Процедура для решения системы линейных уравнений методом Жордана-Гаусса Unit2 i,j,l Счетчики Unit1 prover Промежуточная переменная типа String, используется для проверки наличия букв среди коэффициентов ...
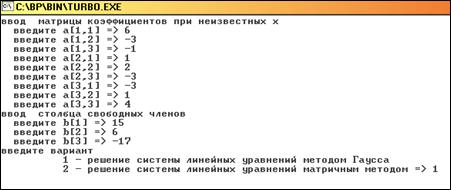
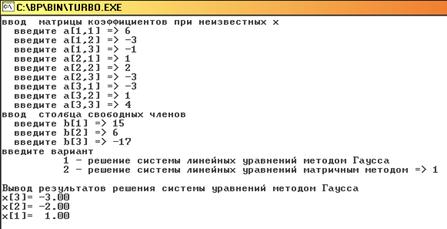
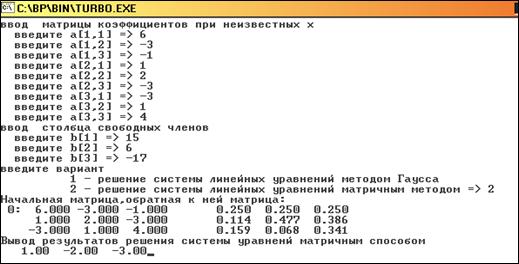

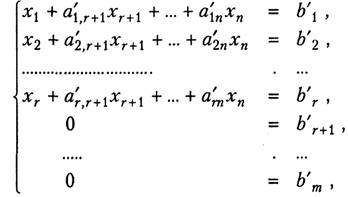

0 комментариев