Навигация
Обозначення та терміни
1.4.2 Обозначення та терміни
Через Ќ* позначається множина всіх кінцевих рядків над алфавітом Ќ, включаючи порожню рядок, що має нульову довжину і е, що позначається. Довжина рядка x позначається |x| . З'єднання, або конкатенація рядків x і у виходить, якщо виписати рядок x, а за нею - рядок у. Конкатенація рядків x і у позначається xy; очевидно |xy| = |x|+|y|.
Говоритимемо, що рядок w - префікс, або початок рядка x, якщо x = wy для деякого у ? Ќ*. Говоритимемо, що рядок w - суфікс, або кінець рядка x, якщо x = yw для деякого у ? Ќ*. Писатимемо w [ x, якщо w - префікс x, і w ] x, якщо w - суфікс x. Наприклад, ab [ abcca і cca ] abcca.
Порожній рядок є префіксом і суфіксом будь-якого рядка; якщо w - префікс або суфікс x, то |w| <= |x|. Для будь-яких рядків x і у і для будь-якого символу а співвідношення x ] у і ха ] уа рівносильні; стосунки ] і [ транзитивні.
Хай x, у і z - рядки, для яких x ] z і x [ z. Тоді x ] у, якщо |x| <= |y|; у ] x, якщо |x| >= |y|, і x = у, якщо |x| = |y|.
Якщо S[1..r] - рядок довжини r, то його префікс довжини до <= r позначатиметься Sk = S[1..k] (зокрема, S0 = е і Sr = S). У цих позначеннях завдання про знаходження зразка P довжини m в тексті T довжини n полягає в знаходженні всіх таких s з проміжку 0 <= s <= n - m, що P ] Ts+m.
1.4.3 Аналіз алгоритму текстового пошуку
Найпростіший алгоритм пошуку зразка P в тексті T послідовно перевіряє рівність P[1..m]= T[s + 1..s + m] для всіх n - m + 1 можливих значень s:
for s = 0 to n - m
if P[1..m]= T[s+1..s+m]
then print «рядок входить із зрушенням» s
Можна сказати, що ми рухаємо зразок уздовж тексту і перевіряємо всі його положення. Відзначимо, що перевірка рівності рядків (P[1..m]= T[s+1..s+m]) є ще одним внутрішнім циклом.
Час роботи приведеної процедури пошуку у гіршому разі є І((n - m + 1)m). Насправді, хай T = an (буква а, повторена n разів), а P = am. Тоді для кожної з n - m + 1 перевірок буде виконано m порівнянь символів, всього (n - m + 1)m, що є І(n2) (при m = n / 2).
Простий алгоритм - не кращий. Неефективність пов'язана з тим, що інформація про текст T, що отримується при перевірці даного зрушення s, ніяк не використовується при перевірці подальших зрушень. Тим часом, така інформація може дуже допомогти. Хай, наприклад, P = aaab і ми з'ясували, що зрушення s = 0 допустимий. Тоді зрушення 1, 2 і 3 свідомо недопустимі, оскільки T[4]= b.
1.4.4 Швидкий алгоритм текстового пошуку
Цей алгоритм, запропонований Кнутом, Морісом і Праттом, працює за час І(n + m). Таке прискорення досягається за рахунок того, що при подальшому пошуку заздалегідь обчислюється спеціальна «префікс-функція» на основі вже відомої інформації.
Префікс-функція, асоційована із зразком P, несе інформацію про те, де в рядку P повторно зустрічаються різні префікси цього рядка. Використання цієї інформації дозволяє уникнути перевірки свідомо неприпустимих зрушень.
Хай простий алгоритм шукає входження підрядка P = ababaca в текст T. Припустимо, що для деякого зрушення s виявилось, що q перших символів зразків збігаються з символами тексту, а в наступному символі є розбіжність, де q = 5). Отже, ми знаємо q символів тексту, від T[s+1] до T[s+q], і з цієї інформації можна укласти, що деякі подальші зрушення будуть свідомо недопустимі.
У загальному випадку префікс-функція повинна відповісти на таке питання:
Хай P[1..q]= T[s + 1..s + q]; яке найменше значення зрушення s` > s, для якого
P[1..k]= T[s` + 1..s` + до](1.1)
де s` + до = s + q.
Число s` - це найменше значення зрушення, більше s, яке не можна відкинути. Щоб знайти s`, нам не потрібно нічого знати про текст T, достатньо знання зразка P і числа q. Саме, T[s` + 1..s` + до] - суфікс рядка Pq. Тому число до у формулі (1.1) - це найбільше число до < q, для якого Pk є суфіксом Pq. Само значення s` обчислюється за формулою s` = s + (q - до).
Префікс-функцией, що асоціюється з рядком P[1..m], називається функція f:{1,2., m} Ќ {0,1., m - 1}, визначена таким чином:
f[q]= max{k:k < q Pk ] Pq}.(1.2)
Іншими словами, f[q] - довжина найбільшого префікса P, що є (власним) суфіксом Pq. Приведемо псевдокод алгоритму Кнута - Моріса - Пратта.
n = length(T)
m = length(P)
q = 0
for i = 1 to n
while q > 0 and P[q+1]< > T[i]
q = pf[q]
if P[q+1]=T[i]
then q = q+1
if q=m
then print «рядок входить із зрушенням» i-m
q = pf(q)
m = length[P]
pi[1]= 0
до = 0
for q = 2 to m
while до > 0 and P[k+1]< > P[q]
до = pi[k]
if P[k+1]=P[q]
then до = k+1
pi[q]= до
return pi
Час виконання префікс - функції пропорційно довжині рядка m і, отже, є O(m). Аналогічно, час виконання операторів процедури пошуку пропорційно довжині підрядка і є O(n). Отже, загальний час виконання приведеного алгоритму є O(m+n), що дає значний виграш в порівнянні з простий процедурою пошуку.
Проаналізувавши два методи пошуку були виявлені як позитивні так і негативні сторони. Для даної роботи необхідний пошукач який працює з невеликим часом і частковим текстом (див. рис. 1.10)

Рисунок 1.10 – Схема роботи програми пошука
Похожие работы
... іла необхідність зміни ролі бібліотеки, вона повинна перетворитися в центр інформаційного й комунікативного забезпечення людей. Розділ ІІ. Основні шляхи автоматизації шкільних бібліотек району На жаль, впровадження нових інформаційних технологій у шкільні бібліотеки поки досить проблематично. Більшість сільських бібліотек на сьогоднішній день взагалі не мають комп'ютерів. Можна виділити два ...
... розділу можна розподілити за десятьма діленнями, тому виникає велика кількість штучних рішень, відбувається нерівномірність наповнення ділень. У той же час застосування в бібліотечно-бібліографічній класифікації десяткових індексів мало велике значення, і їх стали широко використовувати. Такі індекси дають можливість деталізувати систему як це необхідно, подрібнюючи попередні ділення на десять ...
... втілення вже залежить не тільки від прогресу науково-технічної думки, але й від соціально-економічних і правових умов, в яких вони існують. 2.2 Сучасні парадигми інформатизації суспільства в умовах глобалізації Інформатизація сучасного суспільства побудована на певних законах і постулатах, які надають їм постійного явища. У різних наукових напрямах по-різному трактується сучасне інформаційне ...
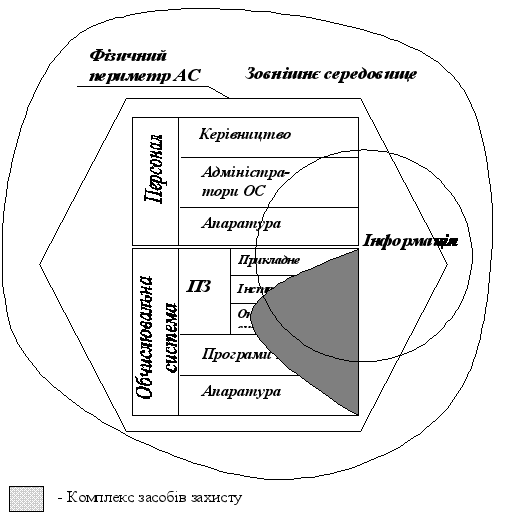
... В АБС АКБ «ПРОМІНВЕСТБАНК» ТА ОЦІНКА РІВНЯ ВРАЗЛИВОСТІ БАНКІВСЬКОЇ ІНФОРМАЦІЇ 3.1 Постановка алгоритму задачі формування та опис елементів матриці контролю комплексної системи захисту інформації (КСЗІ) інформаційних об’єктів комерційного банку В дипломному дослідженні матриця контролю стану побудови та експлуатації комплексної системи захисту інформації в комерційному банку представлена у вигляді ...
0 комментариев